【线段树】BZOJ2752: [HAOI2012]高速公路(road)

2752: [HAOI2012]高速公路(road)

Time Limit: 20 Sec  Memory Limit: 128 MB
Submit: 1621  Solved: 627
[Submit][Status][Discuss]

Description

Y901高速公路是一条重要的交通纽带，政府部门建设初期的投入以及使用期间的养护费用都不低，因此政府在这条高速公路上设立了许多收费站。
Y901高速公路是一条由N-1段路以及N个收费站组成的东西向的链，我们按照由西向东的顺序将收费站依次编号为1~N，从收费站i行驶到i+1(或从i+1行驶到i)需要收取Vi的费用。高速路刚建成时所有的路段都是免费的。
政府部门根据实际情况，会不定期地对连续路段的收费标准进行调整，根据政策涨价或降价。
无聊的小A同学总喜欢研究一些稀奇古怪的问题，他开车在这条高速路上行驶时想到了这样一个问题:对于给定的l,r(l<r),在第l个到第r个收费站里等概率随机取出两个不同的收费站a和b，那么从a行驶到b将期望花费多少费用呢?

Input

第一行2个正整数N,M，表示有N个收费站，M次调整或询问
接下来M行，每行将出现以下两种形式中的一种
C l r v 表示将第l个收费站到第r个收费站之间的所有道路的通行费全部增加v
Q l r   表示对于给定的l,r，要求回答小A的问题
所有C与Q操作中保证1<=l<r<=N

Output

对于每次询问操作回答一行，输出一个既约分数
若答案为整数a，输出a/1

Sample Input

4 5
C 1 4 2
C 1 2 -1
Q 1 2
Q 2 4
Q 1 4

Sample Output

1/1
8/3
17/6

HINT

数据规模

所有C操作中的v的绝对值不超过10000

在任何时刻任意道路的费用均为不超过10000的非负整数

所有测试点的详细情况如下表所示

Test N M

1 =10 =10

2 =100 =100

3 =1000 =1000

4 =10000 =10000

5 =50000 =50000

6 =60000 =60000

7 =70000 =70000

8 =80000 =80000

9 =90000 =90000

10 =100000 =100000

题解

设i到i+1的一段是第i段，如果询问是l~r的话，第i段对答案的贡献为

　　　　　　

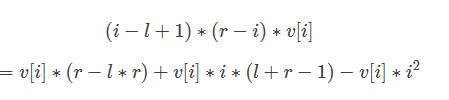
所以我们只需要在线段树里维护i的和，i²的和，v[i]的和，v[i]*i的和，v[i]*i²的和就可以了

代码

 

//by 减维
#include<cstdio>
#include<iostream>
#include<cstring>
#include<queue>
#include<cstdlib>
#include<ctime>
#include<cmath>
#include<map>
#include<bitset>
#include<algorithm>
#define ll long long
#define maxn 100005
#define ls l,mid,v<<1
#define rs mid+1,r,v<<1|1
#define lv v<<1
#define rv v<<1|1
using namespace std;

int n,m;
ll sum[maxn*5][10],ans[10],len[maxn*5],mark[maxn*5],b[maxn],c[maxn];

ll gcd(ll x,ll y)
{
    return y?gcd(y,x%y):x;
}

void upda(int v)
{
    for(int i=0;i<=4;++i)
        sum[v][i]=sum[v<<1][i]+sum[v<<1|1][i];
}

void pd(int v,int l,int r)
{
    if(mark[v]){
        mark[v<<1]+=mark[v];
        mark[v<<1|1]+=mark[v];
        sum[lv][1]+=len[lv]*mark[v];
        sum[lv][2]+=sum[lv][0]*mark[v];
        sum[lv][3]+=sum[lv][4]*mark[v];
        sum[rv][1]+=len[rv]*mark[v];
        sum[rv][2]+=sum[rv][0]*mark[v];
        sum[rv][3]+=sum[rv][4]*mark[v];
        mark[v]=0;
    }
}

void build(int l,int r,int v)
{
    len[v]=r-l+1;
    if(l==r){
        sum[v][0]=l;
        sum[v][1]=0;
        sum[v][2]=0;
        sum[v][3]=0;
        sum[v][4]=(ll)l*l;
        return ;
    }
    int mid=(l+r)>>1;
    build(ls);
    build(rs);
    upda(v);
}

void change(int l,int r,int v,int x,int y,ll val)
{
    if(x<=l&&r<=y){
        mark[v]+=val;
        sum[v][1]+=len[v]*val;
        sum[v][2]+=sum[v][0]*val;
        sum[v][3]+=sum[v][4]*val;
        return ;
    }
    if(mark[v])pd(v,l,r);
    int mid=(l+r)>>1;
    if(x<=mid)change(ls,x,y,val);
    if(y>mid) change(rs,x,y,val);
    upda(v);
}

ll ask(int l,int r,int v,int x,int y,int k)
{
    if(x<=l&&r<=y)return sum[v][k];
    if(mark[v])pd(v,l,r);
    int mid=(l+r)>>1;
    ll anss=0;
    if(x<=mid)anss+=ask(ls,x,y,k);
    if(y>mid) anss+=ask(rs,x,y,k);
    return anss;
}

void print(int l,int r,int v)
{
    if(l==r){
        printf("%lld %lld %lld %lld %lld\n",sum[v][0],sum[v][4],sum[v][1],sum[v][2],sum[v][3]);
        return ;
    }
    int mid=(l+r)>>1;
    print(ls);
    print(rs);
}

int main()
{
    scanf("%d%d",&n,&m);
    build(1,n-1,1);
    char op[5];
    ll l,r,v;
    for(int i=1;i<=m;++i)
    {
        scanf("%s",op);
        if(op[0]=='C'){
            scanf("%lld%lld%lld",&l,&r,&v);
            change(1,n-1,1,(int)l,(int)r-1,v);
        }else{
            scanf("%lld%lld",&l,&r);
            ll x=(r-l+1)*(r-l)/2ll;
            for(int i=1;i<=3;++i)
                ans[i]=ask(1,n-1,1,(int)l,(int)r-1,i);
            ans[0]=ans[1]*(r-l*r)+ans[2]*(l+r-1)-ans[3];
            ll g=gcd(x,ans[0]);
            printf("%lld/%lld\n",ans[0]/g,x/g);
        }
    }
    return 0;
}