Cross-entropy Cost Function for Classification Problem

在Machine Learning的Regression Problem中，常用Quadratic Function来做Cost Function，用以表征Hypothesis与Y之间的差距。而通过Gradient Descent来不断调整参数，从而缩小这个Gap从而训练我们的算法。

 

而在Neural Network的Classification Problem中，如果依然使用Quadratic Function，则会出现学习速率过慢的问题，这时我们就需要选用Cross-entropy来做Cost Function。首先，在NN的Backpropagation过程中，我们可以知道Cost对于最后一层的weight矩阵的梯度为：

 

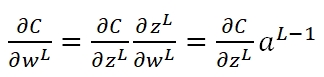
其中C对激励输入z^L的梯度记为：

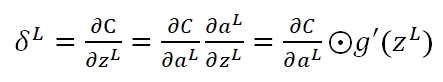
而在使用Quadratic作为Cost的情况下：

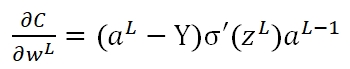
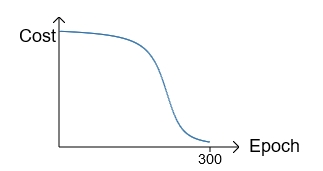
可以看出，该梯度是由Hypothesis与Y的差值以及σ'(z)决定。此时存在一个问题：在训练的最初阶段，我们的参数的随机的，这意味着初期Z值有可能很大，也有可能很小，假如y=0，但由于z值很大导致最终的输出a^L=1，此时预测结果与期望值正好相反，但此时σ的梯度却近似于0，导致学习速率很慢。我们对照下面的两张图即可有所体会：

如果初始值选择的不好，就会是这个情况。在最初训练时，cost下降很慢，当过了某个临界点，学习加快：

然而，我们的期望是，结果差的越多，理应学习速率越快。就像开车出门，如果走了目的地相反的方向，那就要调头呀！而σ'(z)作为斜率，在z很大或很小的地方斜率几乎为零，导致学习速率很慢。所以我们引入一个新的Cost Function：Cross-entropy，其形式如下：

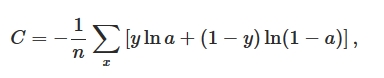
首先，如果我们计算输出cost对第L层第j结点权重ω的偏导（梯度）：

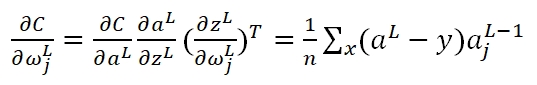
在运算过程中g'(z)被消掉了，也就是说，无论g'(z)是什么情况，不影响我们的梯度，而决定性因素，仅仅是真实输出值与期望值的差。此外，Cost Function变更了，那么在最后一层的δ变更为：

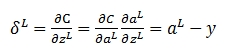
 但在Deep Learning中，其实仅仅一个Cross-entropy是无法解决全部的梯度问题的，在另一篇文章中，我也介绍到了Gradient Vanishing的问题。