高斯判别分析 Gaussian Discriminant Analysis

之前我们分析Logistic Regression，通过求p(y|x)来判定数据属于哪一个输出分类，这种直接判定的方法称为Discriminative Learning Algorithms，但还有另一种思路去接此问题，称为Generative Learning Algorithms，其中包括本文要分析的Gaussian Discriminant Analysis 以及 Naive Bayes。

 

这也给了我们一种思路，当p(y|x)不好求解时，转向p(x|y)，假设p(x|y)服从多维高斯分布，然后对根据分类的类别(如y(0,1))，对两个分类建立高斯模型，而后判定新的数据落在哪个模型的概率更高。从而求解原始问题。

 

首先，两个分类的高斯模型如下，其中涉及到了几个参数，分别代表协方差以及两组数据的数学期望，其实如果我们简化n维高斯到一维就很好理解了。协方差代表数据的离散程度，而数学期望代表数据的中心位置。

 

 

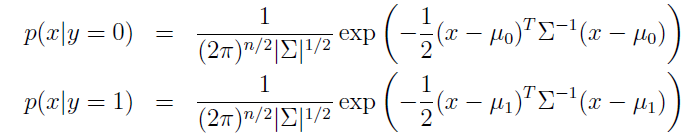
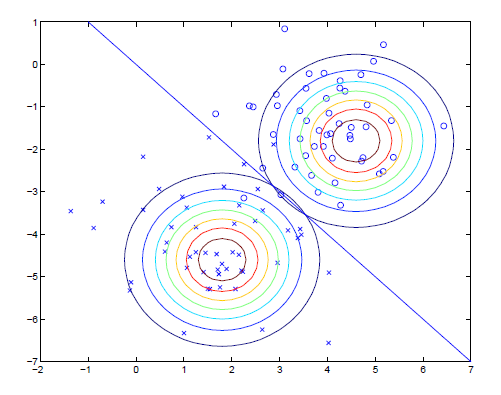
而模型的等高线示意图则如下，可以看到我们在两个分类中，共用了一个协方差

 而后，我们按照贝叶斯公式来求解原问题即可。

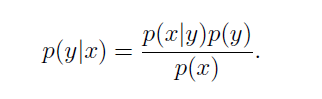
和Logistic Regression相比，GDA需要假设数据符合高斯分布，在此假设的前提下，GDA表现更好，且需要更少的训练数据即可达成效果，但在非高斯分布的情况下，Logistic Regression更佳。