Support Vector Machine(2):Lagrange Duality求解线性可分SVM的最佳边界
在上篇文章《Support Vector Machine(1):线性可分集的决策边界》中,我们最后得到,求SVM最佳Margin的问题,转化为了如下形式:
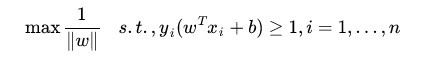
到这一步后,我个人又花了很长的时间去查阅资料,因为数学较差的原因,理解起来相当慢,不过探索的乐趣也就在于不断的打破瓶颈向前,OK继续。上述的问题等价于:
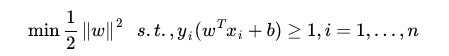
而后我们引入广义拉格朗日函数,利用拉格朗日对偶性来求解此问题。首先明确一下,我们做这些工作的目的是,消去约束条件,为了好求解问题。广义拉格朗日函数为:

上式分为两部分,拉格朗日前辈的思路是,让后一项达到最大值,然后固定住,则问题等价于求前一项的最小值。既然我们想要消去条件(第二项),那么就要证明条件是没用的。也就是说,无论给不给出,这个条件都会成立,那必然就可以舍弃!所以说来,我们考虑,这个世界上只存在两种可能:

首先,我们考虑<1的情况,即不满足原问题的条件,则广义拉格朗日函数的第二项,其最大值会趋于无穷,那么我们没法求该式子的最小值,这个条件也就会被放弃!而在大于等于一的情况下,函数的第二项会趋向于0,也就是说,当我们求整个公式的最小值时,会天然的选择满足条件的一侧,从而将原问题转化为:
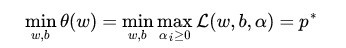
然后我们考虑下一个问题,对偶。刚才,我们先把着眼点放在第二项上,将其最大化,然后再将第一项最小化从而转化了原问题。那么,如果我们再看一下这个公式: 如果将alpha视为常量(取为alpha'),然后将w和b作为变量来最小化这个函数,可知第二项小于等于第一次我们推导的公式。为什么,因为刚才我们把第二项做了max,而现在却是取为alpha',max>=any。也即:
如果将alpha视为常量(取为alpha'),然后将w和b作为变量来最小化这个函数,可知第二项小于等于第一次我们推导的公式。为什么,因为刚才我们把第二项做了max,而现在却是取为alpha',max>=any。也即:

现在确定了w和b,我们再将alpha'来做变换,取最大值,可知:
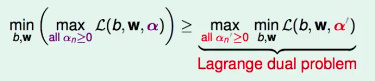
由此得到拉格朗日对偶问题(Lagrange Dual Problem)。

在一般条件下,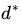 ≤
≤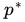 ,但在某些特殊情况下,二者却是等价的,这种情况叫做强对偶。而我们求解SVM的最佳边界,就要用强对偶下的KKT(Karush–Kuhn–Tucker conditions)条件来完成。KKT条件如下:
,但在某些特殊情况下,二者却是等价的,这种情况叫做强对偶。而我们求解SVM的最佳边界,就要用强对偶下的KKT(Karush–Kuhn–Tucker conditions)条件来完成。KKT条件如下:
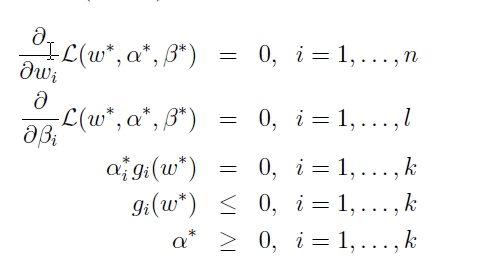
在第三个条件中,我们如果回想,g(w)是什么?可以依稀记得:
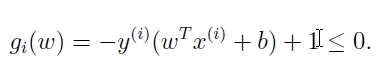
也就是说,此处令alpha>0即g(w)=0的解,是在我们的margin(s)上的,即它们就是support vectors
求解步骤:
1、固定住alpha,对w和b分别求偏导数,让其等于0:
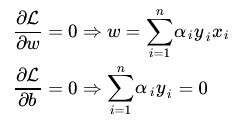
带回之前的L,得到:
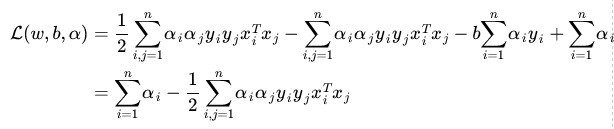
推导过程如下:
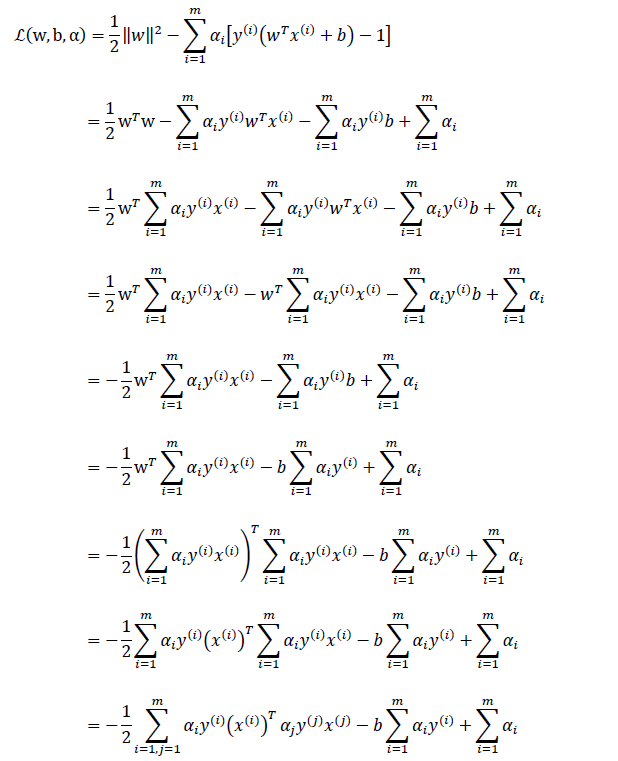
一定要注意x是转置的。为什么a和y不转置?因为a是常数呀,y呢?y是分类呀,-1或者1,所以无需转置。则问题转化为:

利用SMO继续求解的过程,请见:SMO算法
---------------------------------------------------------------------------------------------------------------------------------------
声明几点:
1、要特别感谢这篇文章:简易解说拉格朗日对偶(Lagrange duality),特别喜欢这种平易近人的数学讲解。
2、支持向量机通俗导论写的相当详尽,个人拜读了不下20遍,依然在继续学习中。
3、李航老师的《统计学习方法》中,也讲的很透彻。
我是个看到类似‘拉格朗日’这种字眼就害怕的人,拜谢前人的智慧和分享精神。



