Linear Regression and Gradient Descent
随着所学算法的增多,加之使用次数的增多,不时对之前所学的算法有新的理解。这篇博文是在2018年4月17日再次编辑,将之前的3篇博文合并为一篇。
1.Problem and Loss Function
首先,Linear Regression是一种Supervised Learning,有input X,有输出label y。X可以是一维数据,也可以数多维的,因为我们用矩阵来计算,所以对公式和算法都没有影响。我们期望X经过一个算法hθ(X)=θTX后,得到的结果尽可能接近label y。但在初始状态下,不可能的,所以我们需要Traning Set去训练这个hθ(X)函数。而因为函数的形式是确定的,是线性函数,所以我们通过训练去学习的,其实是参数值θ。
而怎么通过Training Set去学习呢?这里就要引入Cost Function了,其概念是预测值与真实值到底差多少?公式是:
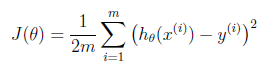
至于这个公式含义,可以从数学上理解认为是把每个training example的差值平方求和,也叫最小二乘法(Mean Square Error, MSE)。从数理统计角度的解释则是,假定Y的值与模型预测值之间从在一个差值ε,这个差值是服从正态分布的,即ε~N(0,σ2)。所以y~N(θTX,σ2)。而后我们对y求最大似然估计(MLE),将最大化MLE的问题,一步步化简,最后也可以得到MSE的结果(公式我不敲了...)。
2.Gradient Descent
下一步是梯度下降 (Gradient Descent),我觉得是machine learning里面最重要的算法之一了。求J(θ)在各个维度上的方向,即偏导数。
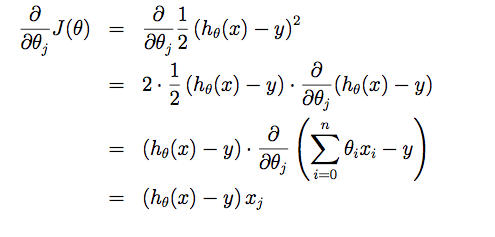
然后同时在n个方向上更新θ:

3. Batch Learning, Stochastic and Mini Batch
可以看到,在上面的算法里,是将m个training example一起计算的,m是training set的大小。也就是每更新一步,我要计算算有training example,复杂度较高。所以有两种变种算法,Stochastic,是每次计算梯度和更新θ时,只用一个training example,同样的问题就是只用一个training example随机性太大,很有可能会路径曲折浪费时间;而Mini Batch则是指定一个Batch_size,比如32,64,每次用一小批,兼顾二者。



