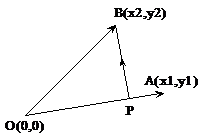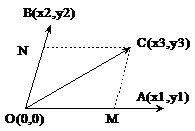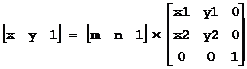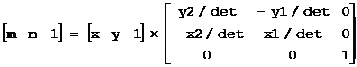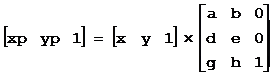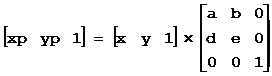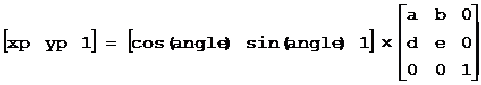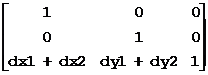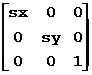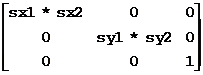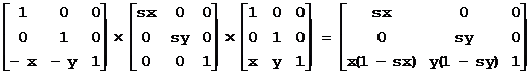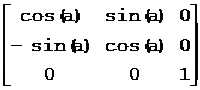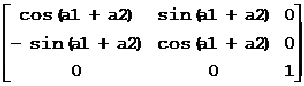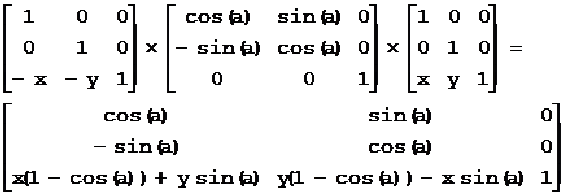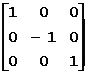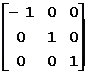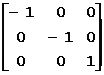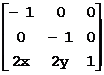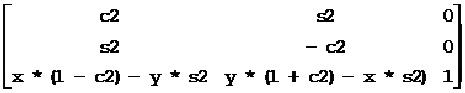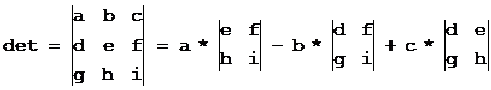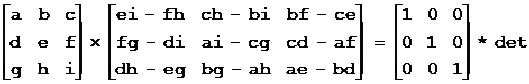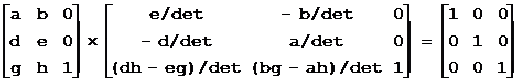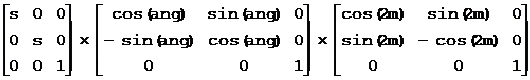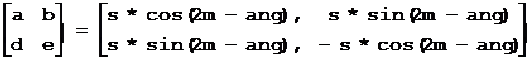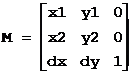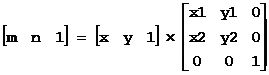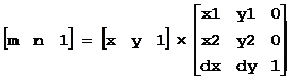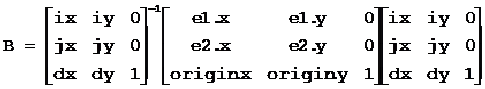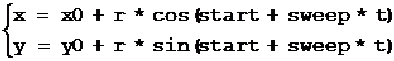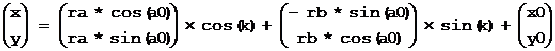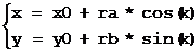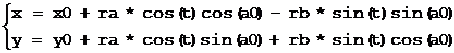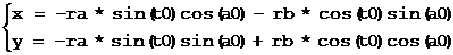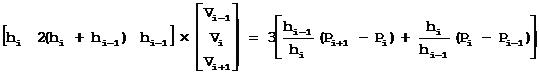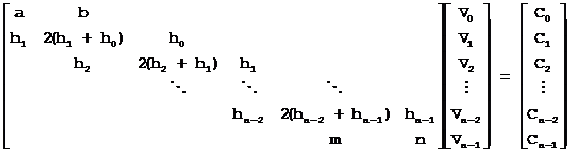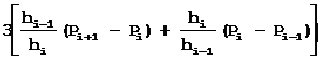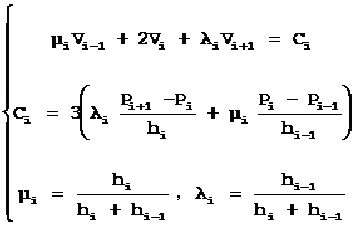二维代数几何原理

张云贵编写于2004年4月，是在为平面CAD软件设计通用SDK时整理所需知识时编写的文档（Word文档见文库）。

第一章 矢量代数

1.1 二维矢量

1.1.1 矢量表示

    矢量的坐标表示为V = (x, y)，其中x和y为坐标分量。

1.1.2 矢量长度

    |V| = sqrt(x*x + y*y)

1.1.3 单位矢量

    E = V / |V|

1.1.4 矢量数乘

    矢量V(x, y)和实数n的数量积为：

            n*V = V*n = ( x * n, y * n )

            V / n = ( x / n, y / n )

1.1.5 矢量点乘

    两个矢量A(x1, y1)和B(x2, y2)的点积为：

            A·B = x1 * x2 + y1 * y2

    性质：

            A·B = B·A

            A·(B+C) = A·B + A·C

    几何意义：

        A·B可以看作|A|乘以B在A上的投影的长度。若A和B为非零矢量，（1）如果A·B＞0，则A和B同在一侧，夹角小于90度；（2）如果A·B＜0，则A和B夹角大于90度；（3）如果A·B=0，则A⊥B。

1.1.6 矢量叉乘

    两个三维矢量A(x1, y1, z1)和B(x2, y2, z2)的叉积为：

        A×B = (y1*z2 – z1*y2, z1*x2 – x1*z2, x1*y2 – y1*x2)

    取z=0可得到二维矢量A(x1, y1)和B(x2, y2)的叉积(0, 0, z)的Z分量为：

        (A×B)_z = x1 * y2 – y1 * x2

    性质：

        A×B = -B×A

        (A+B)×C = A×C + B×C

    几何意义：

        A×B垂直于A和B，且A，B，A×B构成右手系，A×B的矢量长度为以A和B为邻边的平行四边形的面积。(A×B)_z可以看作|A|乘以B在A上的垂直投影的长度。

        若A和B为非零矢量，（1）如果(A×B)_z＞0，则B在A的逆时针方向；（2）如果(A×B)_z＜0，则B在A的顺时针方向；（3）如果(A×B)_z=0，则A∥B。

1.1.7 正交矢量

    沿逆时针方向旋转90度得到矢量V(x, y)的正交矢量：(-y, x)。

    沿顺时针方向旋转90度得到的正交矢量为(y, -x)。

1.1.8 矢量角度

    矢量V(x, y)的角度定义为从坐标系X轴正向旋转到矢量V所转过的角度，逆时针时为正，顺时针为负。矢量角度为：

            angle = acos(x / |V|)，得到的角度范围为0到π

            angle = asin(y / |V|)，得到的角度范围为-π/2到π/2

            angle = atan(y / x)，得到的角度范围为-π/2到π/2

            angle = atan2(y, x)，得到的角度范围为-π到π

    规定零矢量的角度为0。

1.2 矢量点乘和叉乘的应用

1.2.1 矢量夹角

    矢量A(x1, y1)和B(x2, y2)的夹角定义为从矢量A旋转到矢量B所转过的角度，逆时针时为正，顺时针为负。矢量夹角的计算如下：

            sin(angle) = (A×B)_z / (|A|*|B|)

            cos(angle) = (A·B) / (|A|*|B|)

            tan(angle) = (A×B)_z / (A·B)

    得到：

            angle = acos((x1 * x2 + y1 * y2) / (|A|*|B|))

            angle = asin((x1 * y2 – y1 * x2) / (|A|*|B|))

            angle = atan2(x1 * y2 – y1 * x2, x1 * x2 + y1 * y2)

    规定零矢量和其它矢量的夹角为0度。

1.2.2 矢量旋转方向

    要判断矢量A旋转到矢量B旋转角最小时，是逆时针转还是顺时针转，可以这样判断：如果(A×B)_z＞0则是逆时针转，如果(A×B)_z＜0则是顺时针转。

1.2.3 判断平行

    判断两个矢量是否平行就是判断两个矢量的夹角在某个很小的范围内。

    例如满足下面条件时两个矢量就平行：

            tan(夹角) = (A×B)_z / (A·B) ≤ eps

    其中eps=tan(角度公差)，例如0.0001表示角度公差约为0.0057度。

    或者满足下面条件也平行：

            | A/|A| ± B/|B| | ＜ eps

    其中eps=2sin(角度公差/2)，例如0.0001表示角度公差约为0.0057度。

    规定零矢量平行于任何矢量。

1.2.4 判断同向

    满足下面条件时两个矢量就同向：

            (A×B)_z / (A·B) ≤ eps 且 (A·B) ≥ 0

    其中eps=tan(角度公差)，例如0.0001表示角度公差约为0.0057度。

    平行时可能同向也可能反向，因为cos(夹角) = (A·B) / (|A|*|B|)，同向时cos(夹角)接近于1.0，反向时接近于-1.0，考虑到零矢量和任何矢量同向，所以取(A·B) ≥ 0。

    或者满足下面条件也同向：

            | A/|A| － B/|B| | ＜ eps

    其中eps=2sin(角度公差/2)，例如0.0001表示角度公差约为0.0057度。

1.2.5 判断反向

    满足下面条件时两个矢量就反向：

            (A×B)_z / (A·B) ≤ eps 且 (A·B) ＜ 0

    其中eps=tan(角度公差)，例如0.0001表示角度公差约为0.0057度。

    平行时可能同向也可能反向，因为cos(夹角) = (A·B) / (|A|*|B|)，同向时cos(夹角)接近于1.0，反向时接近于-1.0，所以取(A·B) ＜ 0。

    或者满足下面条件也反向：

            | A/|A| ＋ B/|B| | ＜ eps

    其中eps=2sin(角度公差/2)，例如0.0001表示角度公差约为0.0057度。

1.2.6 判断垂直

    满足下面条件时两个矢量就垂直：

            |A·B| ＞ 0 且 (A·B) / (A×B)_z ≤ eps

    其中eps=tan(角度公差)，例如0.0001表示角度公差约为0.0057度。

    或者满足下面条件也垂直：

            |cos(夹角)| = |A·B| / (|A|*|B|) ＜ eps

    其中eps=sin(角度公差)，例如0.0001表示角度公差约为0.0057度。

1.2.7 正交投影

    矢量B(x2, y2)在矢量A(x1, y1)上的投影矢量为OP，垂直距离为|BP|。计算如下：

            proj = (A·B) / (A·A)

            OP = proj * A = A * (A·B)/(A·A)

            PB = OB – OP

    proj > 0 则投影矢量OP和A同向, 否则反向。

            B = OP + PB，OP⊥PB

            OP = A*(A·B)/(A·A)

           

                            正交投影                         矢量分解

1.2.8 矢量分解

    对于两个非零且非共线矢量A(x1, y1)和B(x2, y2)，矢量C(x, y)对A和B的分解如下：

            C = M + N = m*A + n*B

    可以将A和B看作仿射坐标系的坐标轴，(x, y)对应于仿射坐标系下的坐标(m, n)。计算如下（仿射坐标系见后说明）：

           

           

    其中：det = x1*y2 - y1*x2

            m = (x*y2 - y*x2)/det， n = (x1*y – y1*x)/det

    即

            m = (C×B)_z / (A×B)_z ， n = (A×C)_z / (A×B)_z

            M = m * A， N = n * B

 

1.3 二维点

1.3.1 点的表示

    点的坐标表示为P = (x, y)，其中x和y为坐标分量。

1.3.2 矢量运算

    点 + 矢量 = 点

    点 – 矢量 = 点

    点 – 点 = 矢量

    矢量 + 矢量 = 矢量

    矢量 – 矢量 = 矢量

1.3.3 距离和角度

    两点P₁(x1, y1)和P₂(x2, y2)的距离|P₁P₂| = hypot(x2-x1, y2-y1)

    P₁P₂的角度等于矢量P₂ - P₁的角度。

1.3.4 极坐标

    设极点O(x0, y0)，矢径dist，极角angle，则极坐标为：

    (x0 + dist * cos(angle), y0 + dist * sin(angle))

1.3.5 移动直尺法

    设起始点P1(x1, y1)，方向点P2(x2, y2)，沿着方向P1->P2的偏移为xoff，垂直方向（逆时针）的偏移为yoff，则偏移后的坐标P(x, y)为：

            x = x1 + xoff * dcos - yoff * dsin

            y = y2 + xoff * dsin + yoff * dcos

    其中：dcos = (x2 - x1) / |P1P2|，dsin = (y2 - y2) / |P1P2|。

    如果方向点和起始点重合，则偏移后的坐标为(x1+xoff, y1+yoff)。

1.4 二维齐次变换

1.4.1 齐次变换矩阵

    在二维图形的几何变换中的几何变换矩阵可以表示为：

           

    其中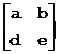：称为M的线性部分，其作用是对图形进行伸缩、旋转、对称等变换；[g, h]称为M的平移部分，其作用是对图形进行平移变换；是对图形进行投影；[i]是对整个图形进行放缩。通常c=0，f=0，i=1。

1.4.2 坐标变换

           

    坐标P(x, y)经变换矩阵变换后坐标为(xp, yp)，有：

            xp = x * a + y * d + g

            yp = x * b + y * e + h

1.4.3 矢量变换

    矢量变换和坐标变换相似，区别是矢量变换不受变换矩阵的平移部分影响。

           

    矢量(x, y)经变换矩阵变换后的矢量为(xp, yp)，有：

            xp = x * a + y * d

            yp = x * b + y * e

    特别的，矢量(1, 0) 变换后的矢量为(a, b)，矢量(0, 1) 变换后的矢量为(d, e)。

1.4.4 角度变换

    角度变换时先将角度转换为单位矢量，然后进行矢量变换，最后得到矢量角度。

           

1.4.5 平移变换

    将一个坐标沿X和Y方向分别平移dx和dy的变换矩阵为：

           

    平移迭加为：

           

1.4.6 比例变换

    以原点为中心，图形的X和Y方向分别变成原来的sx、sy倍的变换矩阵为：

           

    比例迭加为：

           

    sx=sy 时为均匀变化；

    sx=sy > 1时为放大变化；

    0 < sx=sy < 1时为缩小变化。

    以任意点(x, y) 为中心的比例变换矩阵为：

           

1.4.7 旋转变换

    图形绕原点逆时针旋转角度a的变换矩阵为：

           

    图形绕原点顺时针旋转角度a的变换矩阵为：

           

    旋转迭加为：

           

    以任意点(x, y) 为中心的旋转变换矩阵为：

           

1.4.8 对称变换

    关于X轴对称的变换矩阵为：

           

    关于Y轴对称的变换矩阵为：

           

    关于原点对称的变换矩阵为：

           

    关于点(x, y)对称的变换矩阵为：

           

    如果中心线过点(x, y)，倾角为a，则关于直线对称的变换矩阵为：

           

    如果中心线过点(x, y)，方向矢量为(dx, dy)，则关于直线对称的变换矩阵为：

           

    其中：

            d2 = dx * dx + dy * dy， d2相当于矢量长度的平方；

            c2 = 2 * dx * dy / d2， c2相当于cos(2a)，a为中心线倾角；

            s2 = (dx * dx – dy * dy) / d2， s2相当于sin(2a)。

1.4.9 行列式值

    变换矩阵的行列式的值为：

           

    如果c=0，f=0，i=1，则det=ae-bd。

1.4.10 矩阵求逆

    矩阵能求逆矩阵的条件是矩阵的行列式值det不为零。

           

    如果c=0，f=0，i=1，则：

           

1.4.11 正投影变换的分解

    正投影变换由平移、比例、旋转、对称这四种变换组成，要将正投影变换矩阵分解为这四种变换的叠加，可按以下步骤进行：

    （1）正投影变换的条件：变换矩阵的线性部分的行矢量正交且等长。

    设行矢量为e1(a, b)和e2(d, e)，则满足下面条件就是正投影变换：A⊥B 且|e1|=|e2|。判断时可用前面说明的判断垂直的方法给定公差判断。

    （2）正投影变换矩阵的线性部分可以看成由下面的矩阵组成：

           

    其中：s是比例变换部分的比例，ang是旋转部分的角度，m是对称部分的对称中心线倾角。对称部分可能没有，即正投影变换矩阵的线性部分由比例和旋转组成。

    在正投影变换矩阵中，如果a=e且b+d=0，则没有对称部分，否则有。

    比例s = |e1|。

    如果没有对称部分，则旋转角度ang为矢量e1的角度。

    如果有对称部分，则

           

    可以看出，有对称部分时旋转角度ang和对称角度m只能求出(2m-ang)，无法单独求出其中一个。因此，假定旋转角度为零，则对称角度m为矢量e1的角度的一半。

1.5 仿射坐标系

1.5.1 仿射坐标

    给定两个非零且不共线的矢量e1和e2，则任一矢量A可按这两个矢量分解，令其系数为m和n，则矢量A可表示为：

            A = m*e1 + n*e2

    这种坐标系{e1, e2}称为仿射坐标系，e1和e2称为坐标矢量，(m, n)称为矢量A的仿射坐标。

如果仿射坐标系的原点在迪卡尔坐标系中的坐标为origin，则任意点P可表示为：

    P = origin +m*e1 + n*e2

1.5.2 仿射坐标系的矩阵表示

    对于原点为origin(dx, dy)，坐标矢量为e1(x1, y1)和e2(x2, y2)的仿射坐标系{e1, e2, origin}，可用如下变换矩阵表示：

           

    而矢量的仿射坐标用变换矩阵表示如下：

            A = m*e1 + n*e2

           

    点的仿射坐标用变换矩阵表示如下：

            P = origin +m*e1 + n*e2

           

1.5.3 坐标变换

    普通迪卡尔坐标系可以看成原点为(0, 0)，坐标轴矢量为(1, 0)和(0, 1)的坐标系，该坐标系称为世界坐标系，其变换矩阵为单位矩阵。

    仿射坐标系{e1, e2, origin}是以世界坐标系中的矢量e1和e2为坐标轴矢量，以世界坐标系中的坐标origin为原点的坐标系，对应的变换矩阵A表示从该仿射坐标系映射到世界坐标系的矩阵。如果仿射坐标系下的局部坐标为P，则其世界坐标为P×A。

    对于两个仿射坐标系，设其变换矩阵分别为A和B，则前一坐标系到后一坐标系的变换矩阵为AB^-1，该变换矩阵是世界坐标在这两个仿射坐标系中的仿射坐标之间的坐标变换公式。

1.5.4 坐标系映射

    仿射坐标系映射到世界坐标系的线性变换映射关系为：

            T（α）=α×A

    其中：α为齐次仿射坐标。如果在仿射坐标系中建立原点为（0，0），坐标轴矢量为（1，0）（0，1）的坐标系，则A为对应的变换矩阵。如果在仿射坐标系中建立原点为（dx，dy），坐标轴矢量为（ix，iy）（jx，jy）的坐标系，则对应的变换矩阵B=M^-1AM：

           

第二章 参数化曲线

2.1 直线

2.1.1 无穷直线

    过点P0(x0, y0)，方向矢量为V(m, n)的直线参数方程为：

            t∈(-∞, ∞)

    矢量方程为：

            P(t) = P0 + V*t

2.1.2 直线段

    设直线段的端点为A(x0, y0)和B(x1, y1)，则直线段的参数方程为：

            t∈[0, 1]

    矢量方程为：

            P(t) = A + (B-A)*t

2.1.3 射线

    射线的方程和上面的方程相同，只是参数范围为t∈[0, ∞)。

2.1.4 中垂线

    直线段A(x0, y0)B(x1, y1)的中垂线的参数方程为：

            t∈(-∞, ∞)

2.1.5 直线的一般式方程

    直线的一般式方程为：Ax+By+C=0，其中A，B，C为常数，A和B不同时为零。该直线的方向矢量为(-B, A)，斜率为-A/B。

    设两直线L₁和L₂的方程为A₁x+B₁y+C₁=0和A₂x+B₂y+C₂=0，夹角为ang（从L₁到L₂为逆时针时为正），交点为G(x₀, y₀)则有：

            tan(ang) = (A₁B₂-A₂B₁)/(A₁A₂+B₁B₂)

            cos(ang) = (A₁A₂+B₁B₂)/sqrt((A₁²+B₁²)(A₁²+B₁²))

            sin(ang) = (A₁B₂-A₂B₁)/sqrt((A₁²+B₁²)(A₁²+B₁²))

            x₀ = (B₁C₂-B₂C₁)/(A₁B₂-A₂B₁)

            y₀ = (C₁A₂-C₂A₁)/(A₁B₂-A₂B₁)

2.2 圆弧

2.2.1 圆弧方程

      已知圆心C(x0, y0)，半径r，起始角度start，终止角度相对于起始角度的转角sweep（逆时针为正），则圆弧的参数方程为：

            t∈[0, 1]

    设参考X轴矢量为A(sx, sy)，|A|=r，起始角度相对于A，则圆弧的矢量方程为：

            P(t) = A*cos(k) + B*sin(k) + C，k = start + sweep * t，t∈[0, 1]

    其中：A ⊥ B(-sy, sx)，sx²+sy²=r²。

    该圆弧可以看成是在原点为C、X轴矢量为A的直角坐标系中，半径为1、起始角度为start，转角为sweep的圆弧。

    圆的转角为2π，起始角度可定为0。

2.2.2 圆的切线

    给定以下参数方程的圆：

            t∈[0, 2PI]

    则圆上参数为t0的点的切线方程为：

            t∈(-∞, ∞)

2.3 椭圆

2.3.1 椭圆弧方程

    已知椭圆中心(x0, y0)，半长轴ra，半短轴rb，半长轴角度a0，相对于半长轴的起始角度start，终止角度相对于起始角度的转角sweep（逆时针为正），则椭圆弧的参数方程为：

           

    其中：椭圆的离心角k = start + sweep * t，t∈[0, 1]

    如果a0=0则为：

           

    椭圆的转角为2π，起始角度可定为0。

    考虑一般情况，已知椭圆中心C(x0, y0)，共轭半径矢量A(xa, ya)和B(xb, yb)，相对于A的起始角度为start，终止角度相对于起始角度的转角sweep（逆时针为正），则椭圆弧的矢量方程为：

            P(t) = A*cos(k) + B*sin(k) + C，k = start + sweep * t, t∈[0, 1]

    其中：k为椭圆的离心角。

    该椭圆弧可以看成是在原点为C、X轴矢量为A，Y轴矢量为B的仿射坐标系中，半径为1、起始角度为start，终止角度为sweep的圆弧。

2.3.2 椭圆的二次曲线方程形式

    二次曲线为椭圆时，其参数方程为：

            P(t) = (a0 + a1*t + a2*t*t) / (1 + t*t) t∈[0, 1]

    其中：a0，a1，a2是常数矢量。

    对于标准的椭圆方程：

            P(a) = A*cos(a) + B*sin(a) + C

    其中：a为椭圆的离心角；A，B是常数矢量；C为椭圆中心坐标。

    令 t=tan(a/2)，则cos(a)=(1-t*t)/(1+t*t)，sin(a)=2*t/(1+t*t)

            P(t) = ((A+C) + 2B*t + (C-A)*t*t) / (1 + t*t)

    故有：

            a0 = A + C， a1 = 2B， a2 = C - A

2.3.3 椭圆的切线

    给定以下参数方程的椭圆：

            t∈[0, 2PI]

    则椭圆上参数为t0的点P(t0)的切矢P’(t0)为：

           

    如果a0=0则为：

           

    椭圆上参数为t0的点的切线方程为：

            P(t) = P(t0) + P’(t0)*t t∈(-∞, ∞)

2.4 折线

    给定n（n≥2）个有序的顶点P_i（i=0，1，…，n-1），折线有n-1个折线段，每个折线段的方程为：

P_i(t) = P_i + (P_i+1 – P_i)(t – i) 0≤i≤n-1，t∈[i, i+1]

2.5 三次参数样条曲线

2.5.1 三次参数曲线方程

    给定两点P₀和P₁以及这两点的切矢V₀和V₁，设h为弦长|P₀P₁|，则三次参数曲线方程为：

            P(t) = B₀ + B₁t + B₂t² + B₃t³ t∈[0, h]

    其中：

            B₀ = P₀

            B₁ = V₀

            B₂ = 3(P₁ – P₀)/h² – (2V₀ + V₁)/h

            B₃ = (V₀ + V₁)/h² – 2(P₁ – P₀)/h³

    曲线的导数为：

            P’(t) = B₁ + 2B₂t + 3B₃t²

            P”(t) = 2B₂ + 6B₃t

    如果令u = t / h，或者将h看成h=1，则曲线方程可改为

            P(u) = K₀ + K₁u + K₂u² + K₃u³ u∈[0, 1]

    其中：

            K₀ = P₀

            K₁ = V₀

            K₂ = 3(P₁ – P₀) - 2V₀ – V₁

            K₃ = V₀ + V₁ – 2(P₁ – P₀)

    曲线方程又可改写成：

            P(u) = F₀P₀ + F₁P₁ + G₀V₀ + G₁V₁ u∈[0, 1]

    其中：

            F₀ = 2u³ - 3u² + 1

            F₁ = -2u³ + 3u²

            G₀ = u3 - 2u² + u

            G₁ = u³ - u²

2.5.2 三次参数样条函数的连续方程组

    给定n（n≥2）个有序的型值点P_i（i=0，1，…，n-1），构造出第i段三次参数样条曲线为：

            P_i(t) = B₀ + B₁t + B₂t² + B₃t³ i=0，1，…，n-2，t∈[0, h_i]

    其中：

            h_i为弦长|P_iP_i+1|

            B₀ = P_i

            B₁ = V_i

            B₂ = 3(P_i+1 – P_i)/h_i² – (2V_i + V_i+1)/h_i

            B₃ = (V_i + V_i+1)/h_i² – 2(P_i+1 – P_i)/h_i³

    现在已知型值点位置，型值点切矢未知，为了求出型值点切矢V_i，根据曲线在型值点处二阶导数连续的条件得到连续方程组：

           

    其中：i∈[1, n-2]

    该线性方程组共有(n-2)个方程，但有n个未知量V_i，需要添加两个条件。

    连续方程组写成矩阵形式如下：

           

    其中：C_i = ，i=1，2，…，n-2

    该方程组等效于：

            （i=1，2，…，n-2）

2.5.3 端点条件

    连续方程组缺的两个条件通常用边界型值点处的附加条件来提供，常用的端点条件有：

    1）已知边界点处的切矢，该端点也称为夹持端。

        如果给定首端点的切矢V₀，则方程组第一个方程中a=1，b=0，C₀=V₀ 。

        如果给定末端点的切矢V_n-1，则方程组最后一个方程中m=0，n=1，C_n-1=V_n-1 。

    2）已知边界点处的二阶导数为零，该端点也称为自由端。

        如果首端点为自由端，则方程组第一个方程中a=2，b=1，C₀=3(P₁ – P₀)/h₀ 。

        如果末端点为自由端，则方程组最后一个方程中m=1，n=2，C_n-1=3(P_n-1 – P_n-2)/h_n-2 。

    3）已知边界点处为悬臂端。

        如果首端点为悬臂端，则方程组第一个方程中a=1，b=1，C₀=2(P₁ – P₀)/h₀ 。

        如果末端点为悬臂端，则方程组最后一个方程中m=1，n=1，C_n-1=2(P_n-1 – P_n-2)/h_n-2 。

    4）曲线为闭合曲线，首末两端点的位置、切矢、二阶导数相同。

        方程组第一个方程和最后一个方程分别为：

            2(h₀ + h_n-2)V₀ + h_n-2V₁ + h₀V_n-2 = 3(P₁ – P₀)h_n-2/h₀

            V₀ - V_n-1 = 0

2.5.4 累加弦长三次参数样条曲线

    实际应用中，累加弦长三次参数样条曲线对于大挠度曲线的插值拟合效果较好。

    （1）给定n（n≥2）个有序的型值点P_i（i=0，1，…，n-1），建立累加弦长参数：

            h_i = |P_iP_i+1|， s₀ = 0，s_i+1 = s_i + h_i，i=0，1，…，n-2

    由Hermite插值公式，第i段三次参数样条曲线为：

            P_i(t) = P_i(s_i+1 - t)²[2(t - s_i)+ h_i]/ h_i³

                    + P_i+1(t - s_i)²[2(s_i+1 - t)+ h_i]/ h_i³

                    + P_i^’(s_i+1 - t)²(t - s_i)/ h_i²

                    + P_i+1^’(t - s_i)²(t - s_i+1)/ h_i²

            （ t∈[s_i, s_i+1]，i=0，1，…，n-2）

            P_i^’(t) = 6(P_i+1 - P_i)(s_i+1 - t)(t - s_i)/ h_i³

                    + P_i^’(s_i+1 - t)(2s_i + s_i+1 - 3t)/ h_i²

                    + P_i+1^’(t - s_i)(2s_i+1 + s_i - 3t)/ h_i²

            P_i^”(t) = 6(P_i+1 - P_i)(s_i + s_i+1 - 2t)/ h_i³

                    + 2P_i^’(3t - s_i - 2s_i+1)/ h_i²

                    + 2P_i+1^’(3t - s_i+1 - 2s_i)/ h_i²

    （2）建立连续方程组。和三次参数样条曲线方程相同。

        用（u = t + s_i）代换可将累加弦长三次参数样条曲线的方程转换到三次参数样条曲线方程。

2.6 二次参数样条曲线

    给定n（n≥2）个有序的型值点P_i（i=0，1，…，n-1），并设一个参数分割t₀＜t₁＜…＜t_n-2＜t_n-1，称P(t)为二次参数样条曲线，如果：

    （1）在每个区间[t_i-0.5，t_i+0.5]内，P(t)为二次参数曲线，其中：t_i-0.5=（t_i+ t_i+1）/2，t_-0.5= t₀，t_n-0.5= t_n-1，成为半节点。

    （2）在整个区间[t₀，t_n-1]，P(t)具有一阶参数连续，即在半节点t_i-0.5（i=1，2，…，n-1）处成立：

            P^(k)(t_i-0.5-0) = P^(k)(t_i-0.5+0) （k=0，1）

    （3）满足插值条件P(t_i) = P_i （i=0，1，…，n-1）。