洛谷 P2145 [JSOI2007]祖码
题目描述
这是一个流行在Jsoi的游戏,名称为祖玛。
精致细腻的背景,外加神秘的印加音乐衬托,彷佛置身在古老的国度里面,进行一个神秘的游戏——这就是著名的祖玛游戏。祖玛游戏的主角是一只石青蛙,石青蛙会吐出各种颜色的珠子,珠子造型美丽,并且有着神秘的色彩。
环绕着石青蛙的是载着珠子的轨道,各种颜色的珠子会沿着轨道往前滑动,石青蛙必需遏止珠子们滚进去轨道终点的洞里头,如何减少珠子呢?就得要靠石青蛙吐出的珠子与轨道上的珠子相结合,颜色相同者即可以消失得分!直到轨道上的珠子通通都被清干净为止。 或许你并不了解祖玛游戏。没关系。这里我们介绍一个简单版本的祖玛游戏规则。一条通道中有一些玻璃珠,每个珠子有各自的颜色,如图1所示。玩家可以做的是选择一种颜色的珠子(注意:颜色可以任选,这与真实游戏是不同的)射入某个位置。
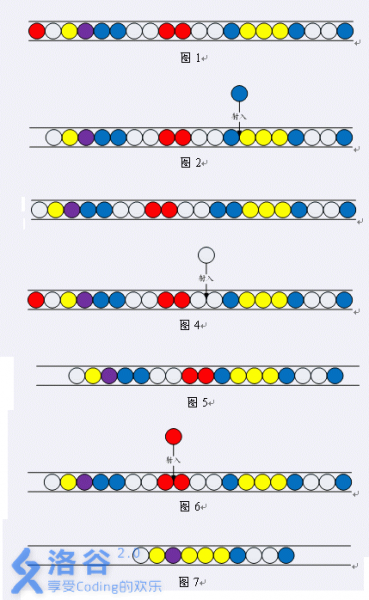
图1 图2中玩家选择一颗蓝色珠子,射入图示的位置,于是得到一个图3的局面。
图2 图3 当玩家射入一颗珠子后,如果射入的珠子与其他珠子组成了三颗以上连续相同颜色的珠子,这些珠子就会消失。例如,将一颗白色珠子射入图4中的位置,就会产生三颗颜色相同的白色珠子。这三颗珠子就会消失,于是得到图5的局面。
图4 图5 需要注意的一点是,图4中的三颗连续的黄色珠子不会消失,因为并没有珠子射入其中。 珠子的消失还会产生连锁反应。当一串连续相同颜色的珠子消失后,如果消失位置左右的珠子颜色相同,并且长度大于2,则可以继续消失。例如,图6中,射入一颗红色珠子后,产生了三颗连续的红色珠子。当红色珠子消失后,它左右都是白色的珠子,并且一共有四颗,于是白色珠子也消失了。之后,消失位置的左右都是蓝色珠子,共有三颗,于是蓝色珠子也消失。最终得到图7的状态。注意,图7中的三颗黄色珠子不会消失,因为蓝色珠子消失的位置一边是紫色珠子,另一边是黄色珠子,颜色不同。
图6 图7 除了上述的情况,没有其他的方法可以消去珠子。 现在,我们有一排珠子,需要你去消除。对于每一轮,你可以自由选择不同颜色的珠子,射入任意的位置。你的任务是射出最少的珠子,将全部珠子消去。
输入输出格式
输入格式:第一行一个整数n(n ≤ 500),表示珠子的个数 第二行n个整数(32位整数范围内),用空格分割,每个整数表示一种颜色的珠子。
输出格式:一个整数,表示最少需要射出的珠子个数。
输入输出样例
说明
据说此题标程有误,致使数据全错....
题解:
和上一道题目一样,设dp[i][j]表示把i~j消掉的最小代价,一开始先将所有相邻且颜色相同的小球合成一个。
套路转移,第一个枚举断点dp[i][j]=min(dp[i][j],dp[i][k]+dp[k+1][j]);二,如果i和j的颜色相同,可以先将中间消掉,再消两端的。dp[i][j]=dp[i+1][j-1]+(num[i]+num[j]>2?0:1);
代码:(有一个点wa了,打表过的)
// luogu-judger-enable-o2 #include <cstdio> #include <iostream> #include <algorithm> #include <cstring> #include <cmath> #include <iostream> #define MAXN 510 #define RG register using namespace std; int dp[MAXN][MAXN],b[MAXN][MAXN]; int a[MAXN],num[MAXN],co[MAXN],n; struct jie{ int l,r; }; void pre(){ int hh=0; for(int i=1;i<=n;i++){ int j=i,now=a[i]; while(a[j]==now) j++; j--; num[++hh]=j-i+1;co[hh]=now; i=j; } n=hh; } int main() { scanf("%d",&n); for(int i=1;i<=n;i++) scanf("%d",&a[i]); pre(); memset(dp,37,sizeof(dp)); for(int i=1;i<=n;i++) if(num[i]>=2) dp[i][i]=1;else dp[i][i]=2; for(int len=2;len<=n;len++){ for(int i=1;i<=n;i++){ int j=i+len-1; if(j>n) continue; if(co[i]==co[j]) dp[i][j]=dp[i+1][j-1]+(num[i]+num[j]>2?0:1); for(int k=i;k<=j;k++) dp[i][j]=min(dp[i][j],dp[i][k]+dp[k+1][j]); } } if(dp[1][n]==3) puts("2"); else printf("%d",dp[1][n]); return 0; }



