05-树9 Huffman Codes及基本操作

哈夫曼树与哈弗曼编码

• 哈夫曼树

带权路径长度(WPL)：设二叉树有n个叶子结点，每个叶子结点带有权值 Wk，从根结点到每个叶子结点的长度为 Lk，则每个叶子结点的带权路径长度之和就是：

　　　　　　WPL =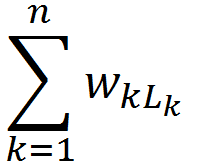

最优二叉树或哈夫曼树: WPL最小的二叉树

• 哈夫曼树的特点:

　　①没有度为1的结点

　　②n个叶子结点的哈夫曼树共有2n-1个结点

　　③哈夫曼树的任意非叶节点的左右子树交换后仍是哈夫曼树

　　④对同一组权值{w1 ,w2 , …… , wn}，存在不同构的两棵哈夫曼树

• 哈夫曼树的构造

每次把权值最小的两颗二叉树合并.(利用堆)

基本操作

• HuffmanTree的建立
• 带权路径的求解
• HuffmanCoding

#include<limits.h> /* INT_MAX等 */
#include<stdio.h> /* EOF(=^Z或F6),NULL */
typedef struct
{
  unsigned int weight;
  unsigned int parent,lchild,rchild;
}HTNode,*HuffmanTree; /* 动态分配数组存储赫夫曼树 */
typedef char **HuffmanCode; /* 动态分配数组存储赫夫曼编码表 */
int min1(HuffmanTree t,int i)
{ /* 函数void select()调用 */
  int j,flag;
  unsigned int k=UINT_MAX; /* 取k为不小于可能的值 */
  for(j=1;j<=i;j++)
    if(t[j].weight<k&&t[j].parent==0)
      k=t[j].weight,flag=j;
  t[flag].parent=1;
  return flag;
}
void select(HuffmanTree t,int i,int *s1,int *s2)
{ /* s1为最小的两个值中序号小的那个 */
  int j;
  *s1=min1(t,i);
  *s2=min1(t,i);
  if(*s1>*s2)
  {
    j=*s1;
    *s1=*s2;
    *s2=j;
  }
}
void HuffmanCoding(HuffmanTree *HT,HuffmanCode *HC,int *w,int n)
{ /* w存放n个字符的权值(均>0),构造赫夫曼树HT,并求出n个字符的赫夫曼编码HC */
  int m,i,s1,s2;
  unsigned c,cdlen;
  HuffmanTree p;
  char *cd;
  if(n<=1)
    return;
  m=2*n-1;
  *HT=(HuffmanTree)malloc((m+1)*sizeof(HTNode)); /* 0号单元未用 */
  for(p=*HT+1,i=1;i<=n;++i,++p,++w)
  {
    (*p).weight=*w;
    (*p).parent=0;
    (*p).lchild=0;
    (*p).rchild=0;
  }
  for(;i<=m;++i,++p)
    (*p).parent=0;
  for(i=n+1;i<=m;++i) /* 建赫夫曼树 */
  { /* 在HT[1~i-1]中选择parent为0且weight最小的两个结点,其序号分别为s1和s2 */
    select(*HT,i-1,&s1,&s2);
    (*HT)[s1].parent=(*HT)[s2].parent=i;
    (*HT)[i].lchild=s1;
    (*HT)[i].rchild=s2;
    (*HT)[i].weight=(*HT)[s1].weight+(*HT)[s2].weight;
  }
  /* 以下为无栈非递归遍历赫夫曼树,求赫夫曼编码*/
  *HC=(HuffmanCode)malloc((n+1)*sizeof(char*));
  /* 分配n个字符编码的头指针向量([0]不用) */
  cd=(char*)malloc(n*sizeof(char)); /* 分配求编码的工作空间 */
  c=m;
  cdlen=0;
  for(i=1;i<=m;++i)
    (*HT)[i].weight=0; /* 遍历赫夫曼树时用作结点状态标志 */
  while(c)
  {
    if((*HT)[c].weight==0)
    { /* 向左 */
      (*HT)[c].weight=1;
      if((*HT)[c].lchild!=0)
      {
        c=(*HT)[c].lchild;
        cd[cdlen++]='0';
      }
      else if((*HT)[c].rchild==0)
      { /* 登记叶子结点的字符的编码 */
        (*HC)[c]=(char *)malloc((cdlen+1)*sizeof(char));
        cd[cdlen]='\0';
        strcpy((*HC)[c],cd); /* 复制编码(串) */
      }
    }
    else if((*HT)[c].weight==1)
    { /* 向右 */
      (*HT)[c].weight=2;
      if((*HT)[c].rchild!=0)
      {
        c=(*HT)[c].rchild;
        cd[cdlen++]='1';
      }
    }
    else
    { /* HT[c].weight==2,退回 */
      (*HT)[c].weight=0;
      c=(*HT)[c].parent;
      --cdlen; /* 退到父结点,编码长度减1 */
    }
  }
  free(cd);
}
void main()
{
  HuffmanTree HT;
  HuffmanCode HC;
  int *w,n,i;
  printf("请输入权值的个数(>1)：");
  scanf("%d",&n);
  w=(int *)malloc(n*sizeof(int));
  printf("请依次输入%d个权值(整型)：\n",n);
  for(i=0;i<=n-1;i++)
    scanf("%d",w+i);
  HuffmanCoding(&HT,&HC,w,n);
  for(i=1;i<=n;i++)
    puts(HC[i]);
}

题目

• Input Specification:

Each input file contains one test case. For each case, the first line gives an integer NN (2\le N\le 632≤N≤63), then followed by a line that contains all the NN distinct characters and their frequencies in the following format:

c[1] f[1] c[2] f[2] ... c[N] f[N]
where c[i] is a character chosen from {'0' - '9', 'a' - 'z', 'A' - 'Z', '_'}, and f[i] is the frequency of c[i] and is an integer no more than 1000. The next line gives a positive integer MM (\le 1000≤1000), then followed by MM student submissions. Each student submission consists of NN lines, each in the format:

c[i] code[i]
where c[i] is the i-th character and code[i] is an non-empty string of no more than 63 '0's and '1's.

• Output Specification:

For each test case, print in each line either "Yes" if the student's submission is correct, or "No" if not.

• Note: The optimal solution is not necessarily generated by Huffman algorithm. Any prefix code with code length being optimal is considered correct.

• Sample Input:

7
A 1 B 1 C 1 D 3 E 3 F 6 G 6
4
A 00000
B 00001
C 0001
D 001
E 01
F 10
G 11
A 01010
B 01011
C 0100
D 011
E 10
F 11
G 00
A 000
B 001
C 010
D 011
E 100
F 101
G 110
A 00000
B 00001
C 0001
D 001
E 00
F 10
G 1

• Sample Output:

Yes
Yes
No
No

AC代码

#include <iostream>  
#include <cstdio>  
#include <vector>  
#include <string>  
using namespace std;
#define MAXSIZE 64  

int nodenum;
int c[64];
char f[64];

typedef struct TNode* HuffTree;
struct TNode
{
	HuffTree left;
	HuffTree right;
	int freq;
};

struct heap
{
	HuffTree* data;
	int size;
	int capacity;
};
typedef struct heap* Minheap;

Minheap CreatHeap()
{
	Minheap H = new struct heap;
	H->data = new HuffTree[MAXSIZE];
	H->size = 0;
	H->capacity = MAXSIZE;
	H->data[0] = new struct TNode;
	H->data[0]->freq = -1;
	return H;
}
bool Insert(Minheap H, HuffTree f)
{
	int i;
	if (H->size == H->capacity){
		printf("minheap is full");
		return false;
	}
	i = ++H->size;
	for (; H->data[i / 2]->freq > f->freq; i /= 2)
		H->data[i] = H->data[i / 2];
	H->data[i] = f;
	return true;
}
bool IsEmpty(Minheap H)
{
	return (H->size == 0);
}

HuffTree DeleteMin(Minheap H)
{
	int Parent, Child;
	HuffTree MinItem, X;

	if (IsEmpty(H)) {
		printf("minheap is empty");
	}

	MinItem = H->data[1];
	X = H->data[H->size--];
	for (Parent = 1; Parent * 2 <= H->size; Parent = Child) {
		Child = Parent * 2;
		if ((Child != H->size) && (H->data[Child]->freq > H->data[Child + 1]->freq))
			Child++;
		if (X->freq <= H->data[Child]->freq) break;
		else
			H->data[Parent] = H->data[Child];
	}
	H->data[Parent] = X;

	return MinItem;
}

HuffTree HuffmanTree()
{
	Minheap h = CreatHeap();
	for (int i = 0; i < nodenum; i++)
	{

		HuffTree f = new struct TNode;
		f->freq = c[i];  //全局变量赋值
		f->left = NULL;
		f->right = NULL;
		if (!Insert(h, f))
			break;
	}
	for (;;)
	{
		if (h->size == 1) break;
		HuffTree f = new struct TNode;
		f->left = DeleteMin(h);
		f->right = DeleteMin(h);
		f->freq = f->left->freq + f->right->freq;
		Insert(h, f);
		//printf("fleft=%d,fright=%d,ffreq=%d\n",f->left->freq,f->right->freq,f->freq);  
	}
	return DeleteMin(h);
}
int WPL(HuffTree tree, int depth)
{
	if ((!tree->left) && (!tree->right))
	{
		//printf("depth:%d,leaf->freq:%d\n",depth,tree->freq);  
		return depth*(tree->freq);
	}
	else
	{
		//printf("depth:%d,tree->freq:%d\n",depth,tree->freq);  
		return WPL(tree->left, depth + 1) + WPL(tree->right, depth + 1);
	}
}

bool check(HuffTree tree, string s)
{
	bool flag = false;
	HuffTree p = tree;
	for (int i = 0; i < s.size(); i++)
	{
		if (s[i] == '0')
		{
			if (!p->left)
			{
				p->left = new TNode;
				p->left->left = NULL;
				p->left->right = NULL;
				p = p->left;
				flag = true;
			}
			else
			{
				p = p->left;
			}
		}
		else if (s[i] == '1')
		{
			if (!p->right)
			{
				p->right = new TNode;
				p->right->left = NULL;
				p->right->right = NULL;
				p = p->right;
				flag = true;
			}
			else
			{
				p = p->right;
			}
		}
	}
	return flag;
}

int main()
{
	int case_;
	cin >> nodenum;
	for (int i = 0; i < nodenum; i++)
	{
		cin >> f[i] >> c[i];
	}
	HuffTree tree = HuffmanTree();
	int wpl = WPL(tree, 0);  //权值可以放在建HufumanTree的时候计算

	cin >> case_;
	for (int j = 0; j < case_; j++)
	{
		HuffTree root = new TNode;
		root->left = NULL;
		root->right = NULL;
		int s_wpl = 0;
		string judge = "";
		for (int i = 0; i<nodenum; i++)
		{
			char ch;
			string s;
			cin >> ch >> s;
			if (s.size()>nodenum - 1){
				judge = "No";
				break;
			}
			s_wpl += s.size()*c[i];

			if (!check(root, s))  //判断序列是否满足要求
				judge = "No";
		}
		if (judge.empty() && s_wpl == wpl)
			judge = "Yes";
		else 
			judge = "No";
		cout << judge << endl;
	}
	return 0;
}

• 补充

//补充，理解思路,时间复杂度O(N*logN)
HuffTree HuffmanTree(Minheap H)
{
	//假设H->size个权值已经在H->data->frq里
	int i;
	HuffTree T;
	BuildMinTree(H); //将H->data[]按权值调整为最小堆
	for (i = 0; i < H->size;i++)
	{
		T = malloc(sizeof(struct TNode));
		T->left = DeleteMin(H); //从最小堆中删除一个结点，作为新T的左子结点
		T->right = DeleteMin(H); //从最小堆中删除一个结点，作为新T的右子节点
		T->freq = T->left->freq + T->right->freq; //计算新权值
		Insert(H, T);
	}
	T = DeleteMin(H);
	return T;
}

题目来源

05-树9 Huffman Codes

Reference

05-树9 Huffman Codes
05-树9 Huffman Codes (用优先队列实现)