二分查找和黄金分割查找

先认识顺序查找：查找效率低。

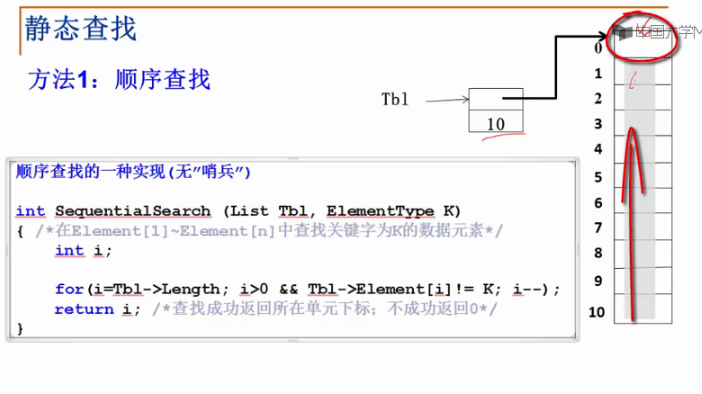
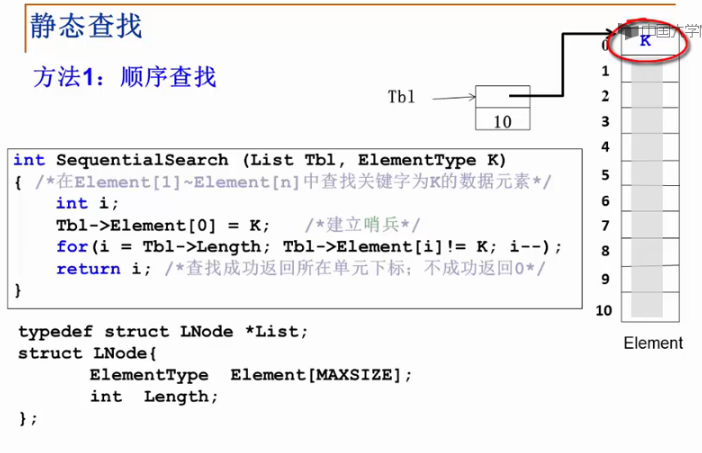
使用哨兵的，可以减少边界结束条件的判断。

二分查找有静态的查找和动态的查找。二分查找效率log(N),但是必须时存储在线性的结构数组中，适合于静态查找；当用二叉判定树的时候，方便数据的插入和删除。

在二分查找中，我们是取mid等于left和right的中间值，即用等分的方法进行查找。

     那为什么一定要等分呐？能不能进行“黄金分割”？也就是mid=left+0.618(right-left),当然mid要取整数。如果这样查找，时间复杂性是多少？也许你还可以编程做个试验，比较一下二分法和“黄金分割”法的执行效率。

测试：

/*!
 * \file 二分查找和黄金查找.cpp
 *
 * \author ranjiewen
 * \date 三月 2017
 *
 * 
 */

#include <stdio.h>
#include <stdlib.h>
#include <time.h>

#define MAXLength 10000000

struct Node {
    int Element[MAXLength];
    int Length;
};
typedef struct Node *List;

clock_t start1, stop1, start2, stop2;
double duration;

int BinarySearch(List Tbl, int K);
int GoldenSearch(List Tbl, int K);

int main()
{
    int i, j, result;
    List Tbl = (List)malloc(sizeof(struct Node));
    Tbl->Length = MAXLength - 1;
    for (i = 0; i < MAXLength; i++){
        Tbl->Element[i] = i;
    }

    start1 = clock();
    for (j = 1; j <= MAXLength - 1; j++){
        result = BinarySearch(Tbl, j);
    }
    stop1 = clock();
    duration = ((double)(stop1 - start1)) / CLK_TCK / (MAXLength - 1);
    printf("Duration of BinarySearch is %6.2es.\n", duration);

    start2 = clock();
    for (j = 1; j <= MAXLength - 1; j++){
        result = GoldenSearch(Tbl, j);
    }
    stop2 = clock();
    duration = ((double)(stop2 - start2)) / CLK_TCK / (MAXLength - 1);
    printf("Duration of GoldenSearch is %6.2es.\n", duration);
    return 0;
}

int GoldenSearch(List Tbl, int K){
    int left, right, mid, NoFound = -1;
    left = 1;
    right = Tbl->Length;
    while (left <= right){
        mid = left + 0.618*(right - left);
        if (K<Tbl->Element[mid]) right = mid - 1;
        else if (K>Tbl->Element[mid]) left = mid + 1;
        else return mid;
    }
    return NoFound;
}
int BinarySearch(List Tbl, int K){
    int left, right, mid, NoFound = -1;
    left = 1;
    right = Tbl->Length;
    while (left <= right){
        mid = (left + right) / 2;
        if (K<Tbl->Element[mid]) right = mid - 1;
        else if (K>Tbl->Element[mid]) left = mid + 1;
        else return mid;
    }
    return NoFound;
}

结果：二分查找的时间要快些。

其中 编程之美之二分查找总结 里面介绍了很多二分查找的坑。二分查找法的实现和应用汇总 之前参考别人的。