队列的顺序存储和链式存储实现
栈和队列是两种特殊的线性表,它们的逻辑结构和线性表相同,只是其运算规则较线性表有更多的限制,故又称它们为运算受限的线性表。栈和队列被广泛应用于各种程序设计中。
队列的基本概念
- 队列(Queue):也是运算受限的线性表。是一种先进先出(FirstIn First Out ,简称FIFO)的线性表。只允许在表的一端进行插入,而在另一端进行删除。
- 队首(front):允许进行删除的一端称为队首。
- 队尾(rear):允许进行插入的一端称为队尾。
例如:排队购物。操作系统中的作业排队。先进入队列的成员总是先离开队列。
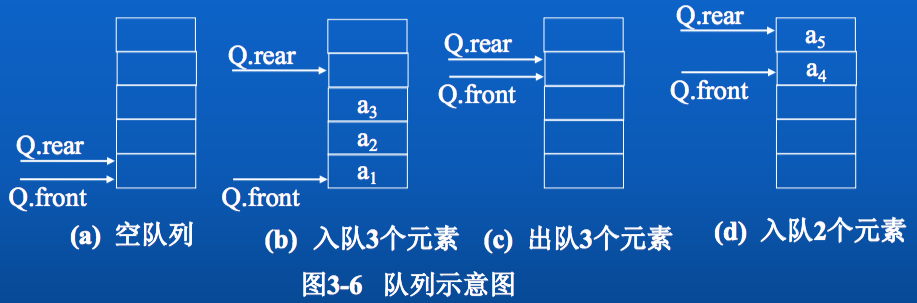
队列中没有元素时称为空队列。在空队列中依次加入元素a1,a2,...,an之后,a是队首元素,an是队尾元素。显然退出队列的次序也只能是a1,a2,...,an即队列的修改是依先进先出的原则进行的。

队列的头尾要分清楚。
对于顺序存储的队列用数组实现,当数组满时,自然过渡到用循环环队列。循环队列实现 为避免队列空和满都是rear=front;方法一:设置Size记录队列大小,tag记录出入队列,;方法二:队列只装N-1个元素。rear指向表尾的下一个元素。
/*! * \file 队列的顺序存储实现.cpp * * \author ranjiewen * \date 2017/03/19 14:30 * * */ #include <stdio.h> #include <stdlib.h> typedef int Position; typedef int ElementType; #define MAXSIZE 10 struct QNode { ElementType *Data; Position front, rear; int MaxSize; }; typedef struct QNode *Queque; Queque CreateQueqe(int maxsize) { Queque Q = (Queque)malloc(sizeof(struct QNode)); Q->Data = (ElementType *)malloc(sizeof(ElementType)*maxsize); Q->front = Q->rear = 0; Q->MaxSize = maxsize; return Q; } bool IsFull(Queque Q) { return (Q->rear + 1) % Q->MaxSize == Q->front; } bool AddQ(Queque Q,ElementType x) { if (IsFull(Q)) { printf("队列满!"); return false; } else { Q->Data[Q->rear] = x; Q->rear = (Q->rear + 1) % Q->MaxSize; } } bool IsEmpty(Queque Q) { return Q->rear == Q->front; } ElementType Delete(Queque Q) { ElementType ret = 0; if (IsEmpty(Q)) { printf("队列空!"); return NULL; } else { ret = Q->Data[Q->front]; Q->front = (Q->front + 1) % Q->MaxSize; return ret ; } } int main() { Queque Q = CreateQueqe(MAXSIZE); for (int i = 9; i > 0;i--) { AddQ(Q, i); } int i = (Q->front); while ( i %Q->MaxSize!=Q->rear) { printf("%d ", Q->Data[i]); i = (i + 1) % Q->MaxSize; } printf("\n"); Delete(Q); Delete(Q); i = (Q->front); while (i %Q->MaxSize != Q->rear) { printf("%d ", Q->Data[i]); i = (i + 1) % Q->MaxSize; } printf("\n"); return 0; }
队列的链式表示和实现
队列的链式存储结构简称为链队列,它是限制仅在表头进行删除操作和表尾进行插入操作的单链表。需要两类不同的结点:数据元素结点,队列的队首指针和队尾指针的结点。栈只是在表头进行插入和删除操作。
/*! * \file 队列的链式存储实现.cpp * * \author ranjiewen * \date 2017/03/19 15:18 * * */ #include<stdio.h> #include <stdlib.h> typedef int ElementType; typedef struct Node *PtrToNode; struct Node { /* 队列中的结点 */ ElementType Data; PtrToNode Next; }; typedef PtrToNode Position; struct QNode { Position Front, Rear; /* 队列的头、尾指针 */ int MaxSize; /* 队列最大容量 */ }; typedef struct QNode *Queue; bool IsEmpty(Queue Q) { return (Q->Front->Next == NULL); } Queue CreateListQueque() //带头结点的操作 { Queue Q; Node *p; p = (PtrToNode)malloc(sizeof(struct Node)); //开辟新节点 p->Next = NULL; Q = (Queue)malloc(sizeof(struct QNode)); Q->Front = Q->Rear = p; return Q; } bool InsertQ(Queue Q, ElementType x) { Node *p; p = (Node*)malloc(sizeof(struct Node)); if (!p) { return -1; } p->Data = x; p->Next = NULL; Q->Rear->Next = p; Q->Rear = p; return true; } ElementType DeleteQ(Queue Q) //带头结点的链式出队列操作 { Position FrontCell; ElementType FrontElem; if (IsEmpty(Q)) { printf("队列空"); return NULL; } else { FrontCell = Q->Front->Next; if (Q->Front->Next == Q->Rear) /* 若队列只有一个元素 */ Q->Front = Q->Rear = NULL; /* 删除后队列置为空 */ else Q->Front->Next = Q->Front->Next->Next; FrontElem = FrontCell->Data; free(FrontCell); /* 释放被删除结点空间 */ return FrontElem; } } void Destroy_Queque(Queue Q) { while (Q->Front!=NULL) { Q->Rear = Q->Front->Next; free(Q->Front); Q->Front = Q->Rear; } } int main() { Queue Q; Q = CreateListQueque(); for (int i = 9; i > 0;i--) { InsertQ(Q, i); } Position temp = Q->Front->Next; while (temp != Q->Rear->Next) { printf("%d ", temp->Data); temp = temp->Next; } printf("\n"); DeleteQ(Q); DeleteQ(Q); while (Q->Front->Next != Q->Rear->Next) { printf("%d ", Q->Front->Next->Data); Q->Front->Next = Q->Front->Next->Next; } printf("\n"); return 0; }
reference:[数据结构]线性结构——队列
C/C++基本语法学习
STL
C++ primer






