4.3.3 算法之美--约瑟夫环的问题
题目:
n个人围成一个圈,每个人分别标注为1、2、...、n,要求从1号从1开始报数,报到k的人出圈,接着下一个人又从1开始报数,如此循环,直到只剩最后一个人时,该人即为胜利者。例如当n=10,k=4时,依次出列的人分别为4、8、2、7、3、10,9、1、6、5,则5号位置的人为胜利者。给定n个人,请你编程计算出最后胜利者标号数。(要求用单循环链表完成。)
第一行为人数n;
第二行为报数k
对于约瑟夫问题当前实现方法大概有两种:
一:模拟:
1.链表模拟
/*! * \file 算法之美--4.3.3 约瑟夫环问题.cpp * * \author ranjiewen * \date 2017/02/25 14:31 * * 单循环链表的使用 */ #include<stdio.h> #include <malloc.h> #include <iostream> using namespace std; #include <list> //使用STL标准库 int Josephusproblem(int n, int m) { if (n<1||m<1) { return -1; } list<int> listInt; for (int i = 0; i < n;i++) { listInt.push_back(i+1); } list<int>::iterator iteCur = listInt.begin(); while (listInt.size()>1) { //前进m-1步 for (int i = 0; i < m - 1;i++) //0开始 { iteCur++; if (iteCur==listInt.end()) { iteCur = listInt.begin();// 循环链表 } } //临时保存删除的节点 list<int>::iterator iteDel = iteCur; if (++iteCur==listInt.end()) { iteCur = listInt.begin(); } cout << *iteDel << " "; listInt.erase(iteDel); } cout << endl; return *iteCur; } typedef struct List { int data; struct List* pNext; struct List(int data_ = 0, struct List* pNext_ = nullptr){ data = data_; pNext = pNext_; } }CirSinglist; int main() { CirSinglist *pHead, *pCur, *pTemp; pHead = (CirSinglist*)malloc(sizeof(CirSinglist)); pCur = pHead; int n, m; printf("请输出 n,m的值:\n"); scanf("%d %d", &n, &m); for (int i = 1; i <= n;i++) //创建链表 { pTemp = (CirSinglist*)malloc(sizeof(CirSinglist)); pTemp->data = i; pTemp->pNext = nullptr; pCur->pNext = pTemp; pCur = pTemp; } pCur->pNext = pHead->pNext; //开始模拟游戏 CirSinglist *p; p = pHead->pNext; while (p->pNext!=p) { for (int i = 1; i < m - 1;i++) //删除节点的前一节点 { p = p->pNext; } //依次删除的数 printf("%d ", p->pNext->data); p->pNext = p->pNext->pNext; //移动指针p p = p->pNext; } printf("\nlast win num:%d \n", p->data); cout << "使用标准库函数:" << endl; cout << "last win :"<<Josephusproblem(n, m) << endl; return 0; }
测试:
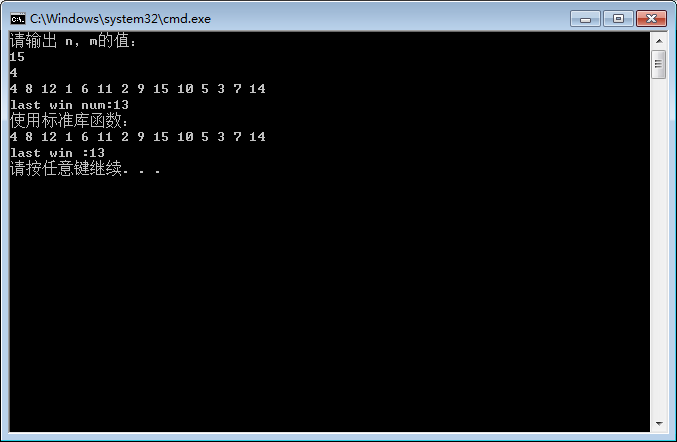
2.数组模拟:
#include<stdio.h> int main() { int n, k; scanf("%d%d", &n, &k); int i; int a[1001]; int dead = 0; //表示已经死了多少人 int num = 0; //num模拟没有被杀的人的喊数 for (i = 1; i<=n; i++) //开始时每个人都可以报数,为了能得到最后一个人的编号,我们让初始值为i下标 { a[i] = i; } for (i = 1;; i++) { if (i > n) { i = i%n; //如果大于总人数,我们就从头开始 } if (a[i] > 0) //如果当前这个人没有死,就报数 num++; if (k == num && dead != n-1) //如果当前这个人报的数等于k 并且没有已经死亡n-1个人 { num = 0; a[i] = 0; dead++; } else if(k == num && dead == n-1) //如果这个人报数等于k,并且已经死了n-1个人,说明当前这个人就是最后的一个活着的了。。 { printf("%d", a[i]); break; } } return 0; }
二、公式法(即递推):
递推过程:
(1)第一个被删除的数为(m-1)%n;
(2)设第二次的开始数字为k,
做下映射:(即将数字的排列计算还是从0开始)
k--->0
k+1--->1
k+2--->2
--- ---
k-2--->n-2
此时剩下n-1个人 ,假如我们已经知道了n-1个人时,最后胜利者的编号为x,利用映射关系逆推,就可以得出n个人时,胜利者的编号为(x+k)%n(要注意的是这里是按照映射后的序号进行的)
其中k=m%n。代入 (x+k)%n<=>(x+(m%n))%n<=>(x%n + (m%n)%n)%n<=> (x%n+m%n)%n <=> (x+m)%n
(3)第二个被删除的数为(m-1)%n-1
(4)假设第三轮的开始数字为o,那这n-2个数构成的约瑟夫环为o,o+1,o+2,...,o-3,o-2。
映射
o--->0
o+1--->1
o+2--->2
--- ---
o-2--->n-3
这是一个n-2个人的问题。假设最后胜利者为y,那么n-1个人时,胜利者为(y+o)%(n-1),其中o等于m%(n-1)。代入可得(y+m)%(n-1)
要得到n-1个人问题的解,只需要得到n-2个人问题的解,倒退下去。只有一个人时,胜利者就是编号0.小面给出递推式:
f(1)=0;
f(i)=(f[i-1]+m)%i;(i>1)
这个公式的思想:
现在假设n=10
0 1 2 3 4 5 6 7 8 9
k=3
第一个人出列后的序列为:
0 1 3 4 5 6 7 8 9
即: 3 4 5 6 7 8 9 0 1(1式)
我们把该式转化为: 0 1 2 3 4 5 6 7 8 (2式)
则你会发现: ((2式)+3)%10则转化为(1式)了
也就是说,我们求出9个人中第9次出环的编号,最后进行上面的转换就能得到10个人第10次出环的编号了
设f(n,k,i)为n个人的环,报数为k,第i个人出环的编号,则f(10,3,10)是我们要的结果
当i=1时, f(n,k,i) = (n+k-1)%n
当i!=1时, f(n,k,i)= ( f(n-1,k,i-1)+k )%n
#include<stdio.h> int main() { int n, m,i,s=0; scanf("%d%d",&n,&m); for(i=2;i<=n;i++) s=(s+m)%i; printf("%d", s+1); return 0; }
说一下:
for(i=2;i<=n;i++)
s=(s+m)%i;
这个式子:
首先从2开始,因为1个人的时候报的数字的人为0号,结果已经确定了。不需要从i=0开始,要注意的是序列从0开始编号的,所以最后的输出结果也要加1.
s表示的是上一轮的结果,m代表是每多少个人出列一次,i代表当前已经出列了多少个人。
整个式子就是根据上一个的出列数和已经出列的人数来算的。
如果还不懂就仔细琢磨哦。
reference:
https://my.oschina.net/871120/blog/309595




