机器学习(Andrew Ng)学习笔记(第9~12章)

神经网络

非线性假设

一般来说，分类问题的数据是非线性可分的，如上图左侧所示，若采用logistic回归分类这些数据，则必须考虑构造高阶特征，如上图右侧所示。

然而，若原始数据包含\(n\)种特征，若想手动构造出二阶特征，则可能构造出大约\(C_n^2=\frac{n(n-1)}2\)个特征，若想构造出更高阶的特征，则特征数目会更多。人工构造高阶特征和训练构造新特征后的数据所需的成本太高。

对于复杂的计算机视觉问题，往往输入数据的维度更高，在这类问题种使用构造高阶特征的logistic回归是完全不可行的。

神经网络单元：感知机

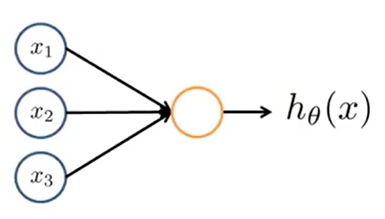
神经网络是由若干层感知机组成的。感知机的结构如上图所示。设输入感知机的列向量\(X=(1,x_1,x_2,\cdots,x_n)^T\)，感知机参数(权重)\(\theta=(\theta_0,\cdots,\theta_n)^T\)，则

\[h_\theta(x)=Sigmoid(\theta^TX) \]

神经网络

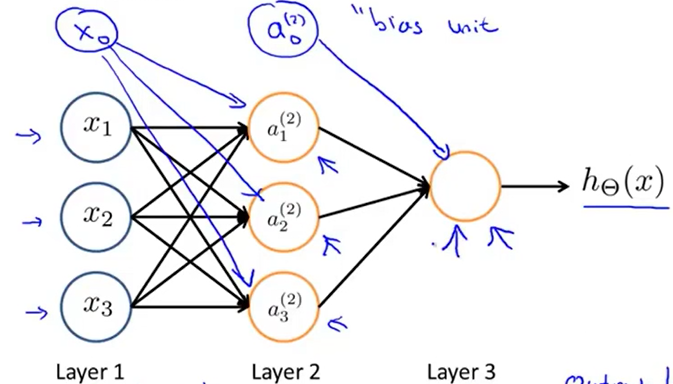
最简单的神经网络结构如上图所示，该网络包含两层感知机(Layer 2,Layer 3),Layer 1为输入层，输入数据。每一层的感知机从上一层接收数据，经处理后向下一层输出

其中，每一层的偏置(图中蓝色)不是感知机，但可以视作特殊的结点，这些结点输出恒为1

符号约定

\(L=\)神经网络的总层数，最少为3

\(s_l=\)第l层的神经元个数(不包括偏置结点)

\(a_i^{(l)}=\)第l层第i个结点的输出值

\(a^{(l)}=(1,a_1^{(l)},\cdots,a_{s_l}^{(l)})^T\)

\(z_i^{(l)}=\)第l层第i个结点从上一层接收数据后加权求和的值，注意这个值还未经激励函数处理

\(z^{(l)}=(z_1^{(l)},\cdots,z_{s_l}^{(l)})^T\)

\(\Theta^{(l)}\)为第l到第l+1层的参数矩阵，大小为\(s_{l+1}\times (s_l+1)\)，\(\Theta^{(l)}_{i,j}=\)第l层第j个结点到第l+1层第i个结点的参数

以下简称激励函数Sigmoid函数为g(x)

为方便描述，虽然偏置结点并不是感知机，但每层偏置结点的输出值仍视为\(a^{(l)}_0\)，另外，虽然第一层输入层并不是由感知机组成的，但我们约定输入数据：1(额外补充的偏置结点),\(x_1,\cdots,x_{s_1}\)为\(a_0^{(1)},\cdots,a_{s_1}^{(1)}\)

前向传播

\[z_i^{(l+1)}=\sum_{j=0}^{s_l}\Theta^{(l)}_{i,j}a^{(l)}_j \]

\[z^{(l+1)}=\Theta^{(l)}a^{(l)} \]

\[a^{(l+1)}=(1,g(z^{(l+1)}))\in \mathbb{R}^{s_{l+1}+1} \]

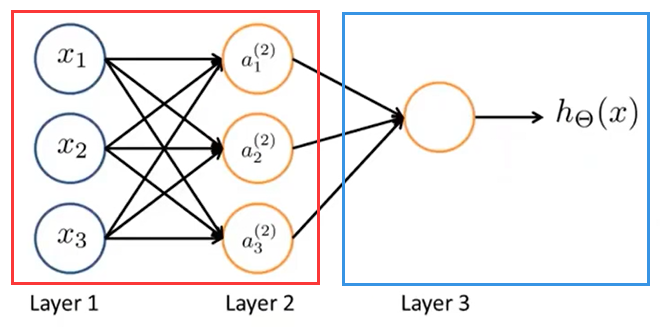
对于上图这个输出层只有一个结点(实现二分类)的神经网络，可以简单概括为，除最后一层外，之前的隐含层实现对输入特征的复杂处理，提取出更适合logistic回归分类的特征，输入到输出层，输出层结点的功能等价于logistic回归，实现对处理过特征的数据的分类。

实例

XOR问题是最经典的线性不可分问题，如上图，输入\(x_1,x_2\in\{0,1\}\)，\(h_\theta(x)=\)两个输入异或得到的结果为1的概率，显然图上的四个样本是无法用线性边界分割的。

XNOR(同或)问题也是线性不可分问题，A XOR B=!(A XNOR B)。为方便起见，下面演示用神经网络实现两个数的XNOR运算

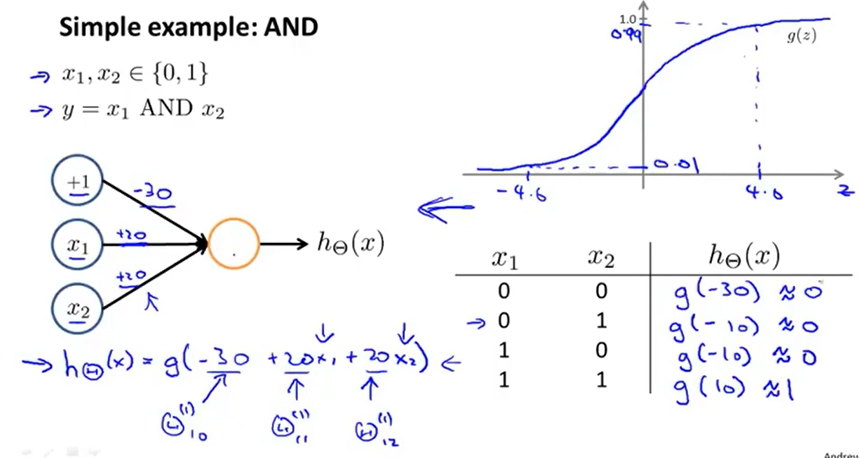
首先考虑用感知机实现AND，取参数\(\theta=(-30,20,20)^T\)即可实现

再考虑用感知机实现OR，取参数\(\theta=(-10,20,20)^T\)即可实现

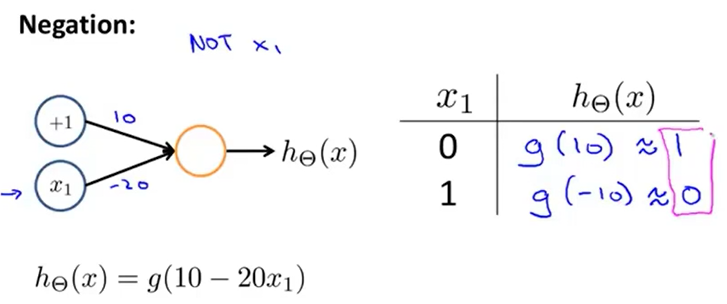
再考虑用感知机实现非运算，取参数\(\theta=(10,-20)^T\)即可实现

已知\(A\odot B=A\cdot B+\bar A \cdot \bar B\)，于是可以用实现x1 AND x2,(NOT x1) AND (NOT x2),x1 OR x2的三个感知机组合实现XNOR运算

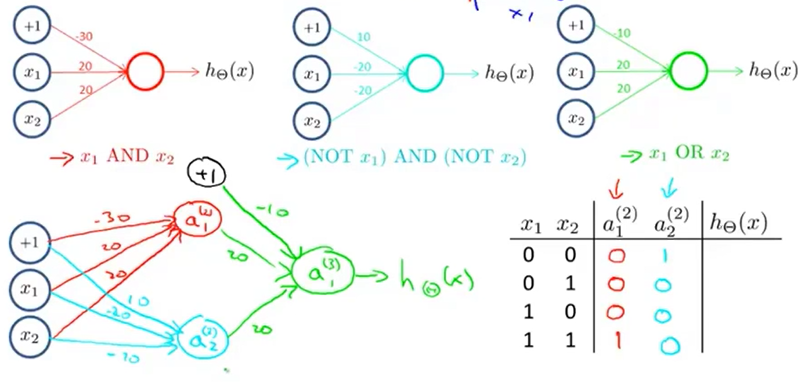
这个例子体现了神经网络实现非线性分割的过程

神经网络实现多元分类

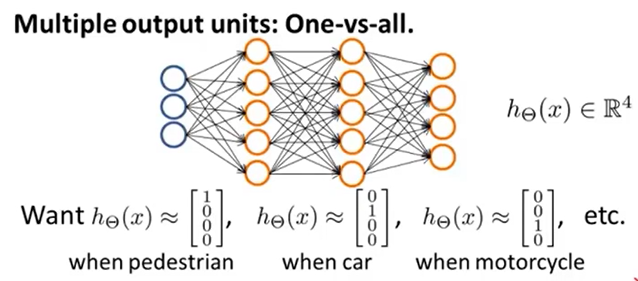
输出层只有一个结点的神经网络可以实现二分类问题，输出值就是\(h_\Theta(x)=P(y=1|x;\Theta)\)(输入数据分类为1的概率)，若要实现K(K>2)分类，只需设置输出层为K个结点，最终输出层第k个结点输出的就是\(P(y=k|x;\Theta)\)(输入数据分类为k的概率)

同时，训练数据的真实输出也要改为，若训练样本标签为第k类，则对应的真实输出中第k个元素为1，其余为0

代价函数

神经网络的代价函数与logistic回归类似，采用交叉熵。不同的是，要把输出层每个结点的输出代价求和，所有参数都要加入到正则化项中：

\[J(\theta)=\frac 1 m \sum_{i=1}^m\sum_{k=1}^K[-y_k^{(i)}log((h_\theta(x^{(i)}))_k)-(1-y_k^{(i)})log(1-(h_\theta(x^{(i)}))_k)]+ \frac \lambda {2m}[\sum_{j=1}^{s_2}\sum_{k=1}^{s_1}(\Theta_{j,k}^{(1)})^2+\sum_{j=1}^{s_3}\sum_{k=1}^{s_2}(\Theta_{j,k}^{(2)})^2]\]

反向传播

设y为输入样本的真实输出向量。若输入样本的真实分类为k，则\(y_k=1\)，否则为0

先考虑代价函数不加正则化：
令：

\[\delta_i^{(l)}=\frac {\partial J(\Theta)}{\partial z_{i}^{(l)}} \]

则有：

\[\delta^{(L)}=a^{(L)}-y \]

\[\delta^{(l)}=(\Theta^{(l)})^T\delta^{(l+1)}.*g'(z^{(l)}) \]

（上步涉及到矩阵求导，证明略去）

\[\frac{\partial J(\Theta)}{\partial \Theta_{i,j}^{(l)}}=\frac{\partial J(\Theta)}{\partial z_j^{(l+1)}}\frac{\partial z_j^{(l+1)}}{\partial \Theta_{i,j}^{(l)}}=\delta_j^{(l+1)}a_j^{(l)} \]

\[\Delta^{l}:=\Delta^{l}+\delta^{l+1}(a^{(l)})^T \]

\(\Delta^{l}_{i,j}\)表示第l层第j个结点到第l+1层第i个结点的参数，对应m个训练样本的梯度之和

则m个样本的平均梯度可以表示为

\[\frac \partial {\partial \Theta_{i,j}^{(l)}}J(\Theta)=\frac 1 m \Delta_{i,j}^{(l)} \]

再给损失函数加入正则化：

\[J(\theta)=\frac 1 m \sum_{i=1}^m\sum_{k=1}^K[-y_k^{(i)}log((h_\theta(x^{(i)}))_k)-(1-y_k^{(i)})log(1-(h_\theta(x^{(i)}))_k)]+ \frac \lambda {2m}[\sum_{j=1}^{s_2}\sum_{k=1}^{s_1}(\Theta_{j,k}^{(1)})^2+\sum_{j=1}^{s_3}\sum_{k=1}^{s_2}(\Theta_{j,k}^{(2)})^2]\]

\[\frac \partial {\partial \Theta_{ij}^{(l)}}J(\Theta)=\frac 1 m \Delta_{ij}^{(l)}+\frac \lambda m \Theta_{ij}^{(l)} \]

反向传播算法伪代码如下：

参数展开

Matlab在调用工具包实现优化过的梯度下降算法时，costFunction()需要接收向量化的\(\Theta,X,y\)，矩阵X向量化为vec可以通过vec=X(:)实现

向量vec复原为矩阵X可用reshape()函数实现

梯度检测

具体实现反向传播的过程中，很难发现求解梯度的过程是否有错误，因此需要用数值估算梯度的方法检验梯度计算是否有误。

\[\frac{d J(\Theta)}{d\Theta_{i,j}^{(l)}}\approx\frac {J(\Theta_{i,j}+\epsilon)-J(\Theta_{i,j}-\epsilon)}{2\epsilon} \]

尽管数值估算梯度很简单，但由于每估算一个参数的梯度需要对整个网络做一次完整的前向传播，因此这一过程速度极慢，真正的反向传播还是只能用公式直接求解梯度

参数随机初始化

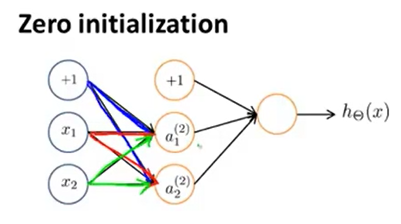
若初始时所有参数\(\Theta_{i,j}^{(l)}\)都为0，由反向传播公式可见，每次在计算梯度时，蓝色的两条边的梯度完全相同，红色、绿色边也是如此。最终训练出的网络中相同参数的边太多，冗余太大。

因此需要随机初始化全部参数\(\Theta_{i,j}^{(l)}\in[-\epsilon,\epsilon]\)。

应用机器学习的建议

评估假设

为了评估学习模型的泛化能力，需要采用交叉验证。即将原始数据集按一定比例分为训练集、交叉验证集与测试集，三个集合一般互不重叠。

使用训练集训练模型，并使用交叉验证集来预测模型在真实数据上的误差，最终用测试集来代表模型在真实数据上的误差。

如果不采用交叉验证，在训练过程中直接用训练集来检验模型的误差，则很难及时发现过拟合问题。

误差度量既可以采用之前提到的交叉熵函数(神经网络、logistic回归)、均方差函数(线性回归)，也可以采用：

\[\mathrm{TestError}=\frac 1 {m_{test}}\sum_{i=1}^{m_{test}} err(h_\theta(x_{test}^{(i)}),y) \]

其中\(err(h_\theta(x_{test}^{(i)}),y)\)，若模型预测结果与真实标签不同，则为1，否则为0

过拟合(高方差)与欠拟合(高偏差)

当模型表达能力太弱时，在训练集和交叉验证集上误差都很大，就是欠拟合(高偏差，high bias)

当模型表达能力太强时，在训练集上误差极小，但在交叉验证集上误差很大，就是过拟合(高方差，high variance)

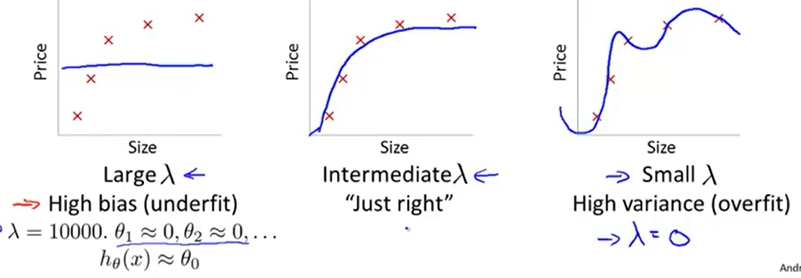
过拟合与欠拟合的经典例子如上图

一般来说，神经网络层数太多、神经元个数太多；正则化参数\(\lambda\)太小或没有正则化；输入数据特征太多；训练数据数目太少都易于过拟合；

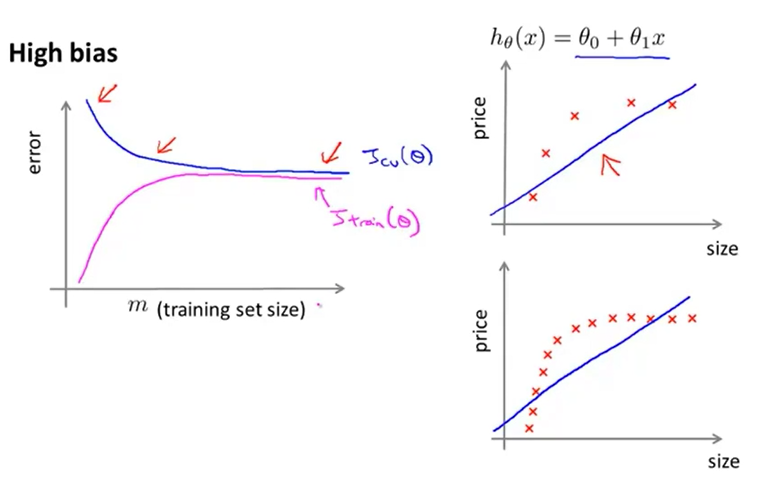
在模型欠拟合时，训练集误差\(J_{train}(\theta)\)和交叉验证集误差训练集误差\(J_{CV}(\theta)\)随训练样本数目增多趋近于某一较大的数值。可见，模型欠拟合时，增加训练样本数目无法减小误差

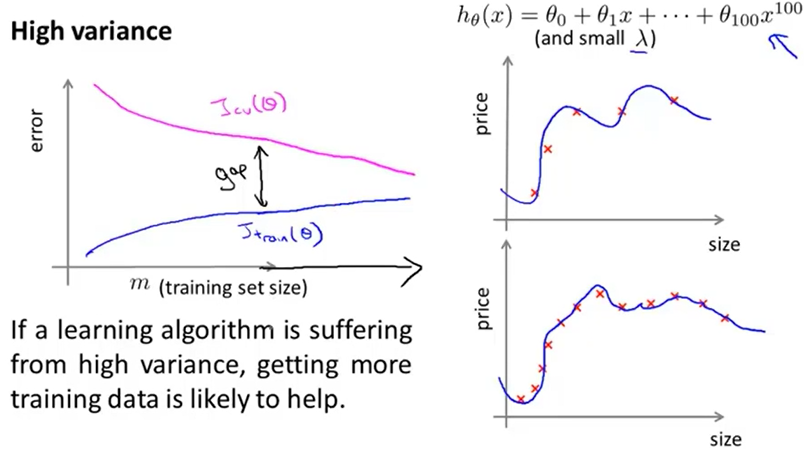
在模型过拟合时，训练集误差\(J_{train}(\theta)\)和交叉验证集误差训练集误差\(J_{CV}(\theta)\)差距较大，但随训练样本数目增多趋近于某一较小的数值。可见，模型过拟合时，增加训练样本数目可以解决过拟合问题，减小误差

决定下一步做什么

当模型过拟合时，可以：

• 1. 增加训练数据
• 2. 减少特征数目
• 3. 增加正则化参数\(\lambda\)

当模型欠拟合时，需要增强模型表达能力，可以：

• 1. 构造更多的特征(如添加高阶多项式特征)
• 2. 增加特征数目
• 3. 减小正则化参数\(\lambda\)

机器学习系统设计

不对称性分类的误差估计

在二分类问题中，对于一些偏斜数据集(skewed classes),一类样本数目占比很大，另一类样本数目占比很小

例如在癌症诊断问题中，实际上只有0.5%的病人患癌，假设当前的模型\(h_\theta(x)\)错误率为1%(99%的判断都是正确的)，现在考虑新的\(h'_\theta(x)=0\)，即不论什么样本，都会给出不患癌的结论，则此时错误率仅为0.5%，比\(h_\theta(x)\)更好。但显然\(h'_\theta(x)\)是一个完全不靠谱的模型。

在这类偏斜数据集的二分类问题中，需要引入新的模型评价标准：Precision准确率(查准率)，Recall召回率(查全率)

首先约定：

• 样本中出现比例少的那一类为Positive(阳性),出现比例多的那一类为Negative(阴性)

• TP=True Positive,预测为Positive并且预测正确的个数

• TN=True Negative,预测为Negative并且预测正确的个数

• FP=False Positive,预测为Positive并且预测错误的个数

• FN=False Negative,预测为Negative并且预测错误的个数

\[Precision=\frac {TP}{TP+FP} \]

\[Recall=\frac {TP}{TP+FN} \]

准确率越高，表明模型对阳性样本的预测越准；召回率越高，表明模型对阳性样本查得越全

一般准确率与召回率是负相关的，很难同时达到极高的准确率和召回率。为了平衡模型的准确率和召回率，需要用F1 Score来量化：

\[F_1=2\frac {Precision·Recall}{Precision+Recall} \]

F1 Score高的模型，达到了准确率与召回率更好的平衡