机器学习(Andrew Ng)学习笔记(第1~8章)

一、监督学习(Supervised Learning)

监督学习的定义：
给出一组数据集，数据集中每一个样本都有对应的正确的输出值。

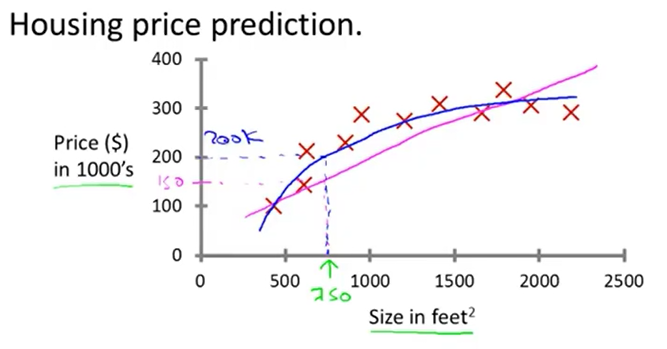
上图是监督学习的最简单的例子之一：回归问题(regression problem)

使用一次函数或更高次的函数拟合房屋售价数据，训练数据中每一个样本都包含了该房子真实的售价，学习目标是预测某一面积(图中绿色的250)的房子的售价(图中蓝色的200K dollar)。

在回归问题中，输入数据与输出值都是连续(continual)的。

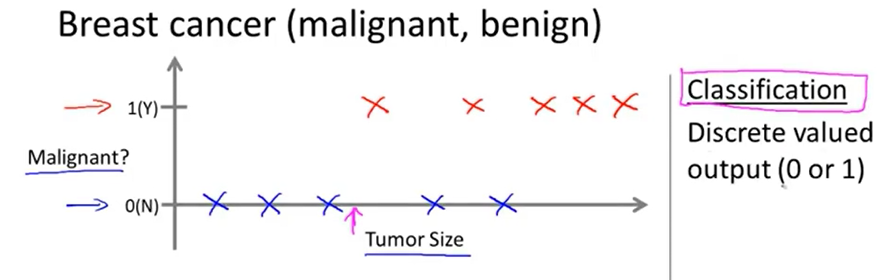
上图是另一个监督学习的例子：分类问题(classification problem)

在这个例子中，给出一组训练数据，其中每个样本包括肿瘤的大小、这个肿瘤是否是恶性的(该样本所属类别)，使用这组训练数据训练一个学习模型，将某个肿瘤的大小输入到学习模型中，让它输出这个肿瘤是良性的还是恶性的。

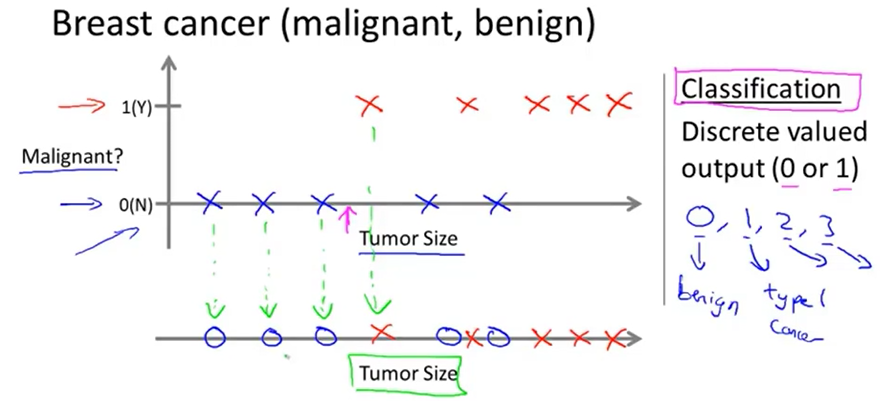
在上图中，训练数据也可以这样表示：用不同类型的点(×、○等)代表不同类别的样本

如上图所示，在其他的分类问题中，训练数据往往有多种特征(如图中的病人的年龄、肿瘤大小)

在分类问题中，输出值是离散的，而且输出值可能不只是本例中0、1(良性、恶性)两种取值，往往可能有两个以上的取值。

课后习题：

问题1：目前已有同一种商品的大量库存，预测这种商品在未来三个月中的售出量

问题2：给出若干个个人账户的信息，判断每个账户是否已被入侵。

显然问题1是回归问题，问题2是分类问题。

二、无监督学习(Unsupervised Learning)

在无监督学习中，给出一组数据集，数据集中每个样本没有对应的标签(类别)。

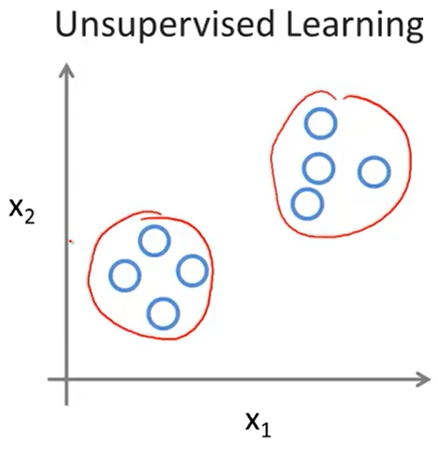
无监督学习的最典型例子：聚类问题(clustering problem)

在聚类问题中，聚类算法需要把输入的数据样本分为若干个簇(cluster)，每个簇中的样本的特征是相似的。

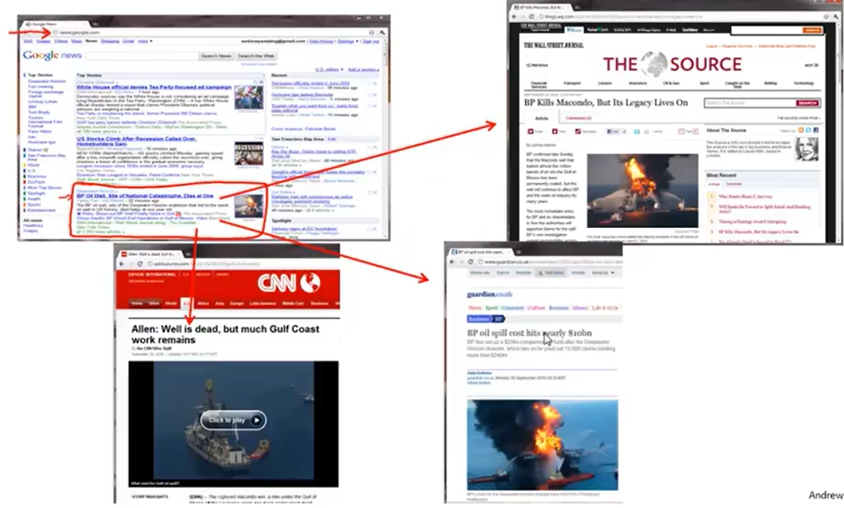
聚类问题的应用一：Google News，Google News把海量的新闻信息分成若干个专题，每个专题中的新闻的相关度很高

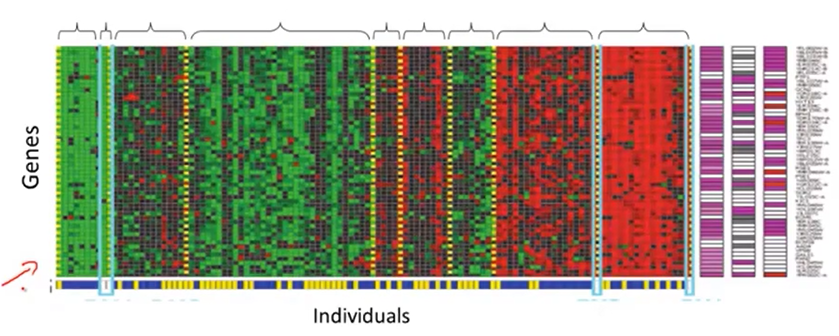
聚类问题的应用二：给出若干个人的DNA微阵列数据，数据中包含该人每种基因的表达程度，通过聚类算法把这些人划分到若干类中，每一类中的人的基因表达情况相似

聚类算法还被应用于高性能计算机集群、社交网络、市场客户划分、天文学(分析星系形成，神TM 666)

鸡尾酒会问题(cocktail party problem)是另一种典型的聚类问题。在一个酒会上，若干个人同时在讲话，他们的声音被安置在不同位置的麦克风录下，鸡尾酒会算法可以从这些麦克风的录音中分离出每个人的声音。

课后习题：
显然只有B和C属于非监督学习任务，因为B和C的数据没有标签，而A和C的训练数据有标签

二、单变量线性回归

1、单变量线性回归的假设函数

对于m个点\((x^{(i)},y^{(i)})\)构成的数据集，我们可以用一个线性函数\(h_\theta(x)=\theta_0+\theta_1x\)来拟合它，这里h表示hypothesis(假设)。

更一般性的，令二维列向量\(\theta=(\theta_0,\theta_1)^T,X^{(i)}=(1,x^{(i)})^T\)，则

\[h_\theta(X)=\theta^TX \]

2、单变量线性回归的误差估计函数

误差估计函数是一个关于参数\(\theta_0,\theta_1\)的函数\(J(\theta)\)。这里的误差估计函数为均方差函数：

\[J(\theta)=\frac 1 {2m}\sum_{i=1}^m(\theta_0+\theta_1x^{(i)}-y^{(i)})^2=\frac 1 {2m}\sum_{i=1}^m(h_\theta(X^{(i)})-y^{(i)})^2 \]

3、梯度下降法求解单变量线性回归参数

单变量线性回归的误差估计函数\(J(\theta)\)一般是一个碗状的凸函数，因此，若任意取初始的\(\theta_0,\theta_1\)，每次迭代时沿着与该点梯度相反的方向走，就能达到全局最优点。

梯度下降公式推导：

\[J(\theta)=\frac 1 {2m}\sum_{i=1}^m(\theta_0 +\theta_1 x^{(i)}-y^{(i)})^2 \]

\[\frac{\partial J(\theta)}{\partial \theta_0}= \frac 1 m \sum_{i=1}^m(\theta_0 +\theta_1 x^{(i)}-y^{(i)}) \]

\[\frac{\partial J(\theta)}{\partial \theta_1}= \frac 1 m \sum_{i=1}^m(\theta_0 +\theta_1 x^{(i)}-y^{(i)})x^{(i)} \]

梯度下降过程中，每次迭代时计算出\(J(\theta)\)对每个参数的偏导数，然后同时更新\(\theta_0,\theta_1\)(学习率为\(\alpha\))：

\[\theta _0 := \theta _0- \alpha \frac{\partial J(\theta)}{\partial \theta_0} \]

\[\theta _1 := \theta _1- \alpha \frac{\partial J(\theta)}{\partial \theta_1} \]

多变量线性回归

1、多变量线性回归的假设函数

在多变量线性回归问题中，每个数据的特征是n维(n>1)而非一维的，则第i个数据可以视为点\((x_1^{(i)},x_2^{(i)},\cdots,x_n^{(i)},y^{(i)})\)，

若令\(\theta=(\theta_0,\theta_1,\cdots,\theta_n)^T,X=(x_0,x_1,x_2,\cdots,x_n)^T=(1,x_1,x_2,\cdots,x_n)^T\)，\((x_0=1)\)，则对应的假设函数

\[h_\theta(X)=\sum_{j=0}^n \theta_jx_j=\theta^TX \]

2、多变量线性回归的误差估计函数

类似于单变量线性回归，多变量线性回归的误差估计函数\(J(\theta)\)为：

\[J(\theta)=\frac 1 {2m}\sum_{i=1}^m(h_\theta(X^{(i)})-y^{(i)})^2=\frac 1 {2m}\sum_{i=1}^m(\theta^TX^{(i)}-y^{(i)})^2 \]

3、梯度下降法求解多变量线性回归参数

\[\frac{\partial J(\theta)}{\partial \theta_t}= \frac 1 m \sum_{i=1}^m(\theta^TX^{(i)T}-y^{(i)})x_t^{(i)}\]

每次迭代时，先计算出\(J(\theta)\)对每个参数的偏导数，然后同时更新所有参数(学习率为\(\alpha\))：

\[\theta _t := \theta _t- \alpha \frac{\partial J(\theta)}{\partial \theta_t} \]

Logistic回归

1、Logistic回归的假设函数

线性回归是为了拟合数据，而Logistic回归是为了分类数据。在最简单的二分类的Logistic回归中，给出了m组数据点\((x^{(i)}_1,\cdots,x^{(i)}_n;y^{(i)})\)，其中\(y^{(i)}\)是离散的，要么为0(负样本)，要么为1(正样本)。

假设函数\(h_\theta(x)\)(hypothesis function)可以输出输入样本x分类为1的概率，即

\[h_\theta(X)=P(y=1|X;\theta)\in[0,1] \]

为了将函数输出值压缩到[0,1]内，这里引入了激励函数Sigmoid,$$g(x)=Sigmoid(x)=\frac 1 {1+e^{-x}}$$

Fig. Sigmoid函数图像

设\(X=(1,x_1,\cdots,x_n)^T,\theta=(\theta_0,\theta_1,\cdots,\theta_n)^T\)，则

\[h_\theta(X)=g(\theta^TX)=\frac 1 {1+e^{-\theta^TX}} \]

当\(h_\theta(X)\geq 0.5\)时表明X所属分类为1，否则X所属分类为0

2、Logistic回归的决策边界

刚刚的表述可以转化为：当\(\theta^TX\geq 0\)时表明X所属分类为1，否则X所属分类为0，此时方程\(\theta^TX= 0\)就是一个决策边界

例如若特征数目为2时，参数\(\theta=(-3,1,1)^T\)，则决策边界如粉红色直线所示

当数据点不能被线性分割时，有时可以构造非线性的决策边界来划分。如下图，正样本和负样本可以用一个圆形决策边界划分，将样本的特征映射到二阶：\((1,x_1,x_2,x_1^2,x_2^2)\)，\(\theta^T X=0\)就是一个二次型，取\(\theta=(-1,0,0,1,1)^T\)，则\(\theta^T X=0\)就是一个圆，\(\theta^T X\geq 0\)时数据点在圆的外侧，表明为正样本，否则点在圆的内侧，为负样本

如果我们把数据特征映射到更高阶，则可以用更复杂的非线性边界来分割正、负样本

3、Logistic回归的代价函数

由于logistic回归引入了Sigmoid函数，该函数是非线性的，所以如果沿用线性回归的均方差损失函数的话，\(J(\theta)\)将是一个非凸的复杂曲线，不利于后面的凸优化

Logistic回归采用交叉熵函数作为损失函数

\[J(\theta)=\frac 1 m \sum_{i=1}^m[-y^{(i)}log(h_\theta(X^{(i)}))-(1-y^{(i)})log(1-h_\theta(X^{(i)}))] \]

\(y^{(i)}=0\)时，\(J(\theta)=-\frac 1 m \sum_{i=1}^mlog(1-h_\theta(X^{(i)}))\)，此时\(J(\theta)\to 0(h_\theta(X^{(i)})\to 0)\),\(J(\theta)\to +\infty(h_\theta(X^{(i)})\to 1)\)

\(y^{(i)}=1\)时，\(J(\theta)=-\frac 1 m \sum_{i=1}^mlog(h_\theta(X^{(i)}))\)，此时\(J(\theta)\to 0(h_\theta(X^{(i)})\to 1)\),\(J(\theta)\to +\infty(h_\theta(X^{(i)})\to 0)\)

这样的误差函数是凸函数，有利于之后的凸优化。

4、梯度下降求Logistic回归的参数

\[Sigmoid'(x)=Sigmoid(x)(1-Sigmoid(x)) \]

\[\frac{\partial J(\theta)}{\partial \theta_t}=\frac 1 m \sum_{i=1}^m\ [-y^{(i)}\frac {g(\theta^T X^{(i)})(1-g(\theta^T X^{(i)}))}{{h_\theta(X^{(i)})}}-(1-y^{(i)})\frac {-g(\theta^T X^{(i)})(1-g(\theta^T X^{(i)}))}{1-h_\theta (X^{(i)})}]x_t^{(i)} \]

\[=\frac 1 m \sum_{i=1}^m\ [-y^{(i)}(1-g(\theta^T X^{(i)}))+(1-y^{(i)})g(\theta^T X^{(i)})]x_t^{(i)} \]

\[=\frac 1 m \sum_{i=1}^m\ (g(\theta^T X^{(i)})-y^{(i)})x_t^{(i)} \]

5、多分类的Logistic回归

对于K分类(K>2)的分类问题，可以构造K个分类器，第K个分类器的假设函数\(h_\theta(X)=P(y=K|X;\theta)\)，即，其输出的是样本分类为K的概率。用K分类的logistic回归对输入样本分类，只需输出预测概率最大的那个分类即可。

正则化

带正则化的线性回归

代价函数

\[J(\theta)=\frac 1 {2m}\sum_{i=1}^m(\theta^TX^{(i)T}-y^{(i)})^2+\frac \lambda {2m}\sum_{i=1}^m \theta_i^2 \]

注意代价函数中的正则化项不包括\(\theta_0\)，\(\theta_0\)不需要正则化

其中\(\lambda\)是非负的惩罚系数，\(\lambda\)越大，最终\(\frac \lambda {2m}\sum_{i=1}^m \theta_i^2\)越小，\(h_\theta(x)\)越接近\(\theta_0\)，表达能力越弱，越倾向于欠拟合。

\(\lambda\)越小，最终\(\frac \lambda {2m}\sum_{i=1}^m \theta_i^2\)越大，\(h_\theta(x)\)越复杂，表达能力越强，越倾向于过拟合。

梯度下降

对于第t个参数\(\theta_t\)，其更新公式为：

\[\theta _t := \theta _t- \alpha \frac{\partial J(\theta)}{\partial \theta_t} \]

\[\frac{\partial J(\theta)}{\partial \theta_0}= \frac 1 m \sum_{i=1}^m(\theta^TX^{(i)T}-y^{(i)})x_0^{(i)},t=0\]

\[\frac{\partial J(\theta)}{\partial \theta_t}= \frac 1 m \sum_{i=1}^m(\theta^TX^{(i)T}-y^{(i)})x_t^{(i)}+\frac \lambda m \theta_t,t\geq1\]

在梯度下降的过程中可见，t>=1时有：

\[\theta_t:=\theta_t(1-\alpha \frac \lambda m)- \frac 1 m \sum_{i=1}^m(\theta^TX^{(i)T}-y^{(i)})x_t^{(i)},t\geq1\]

其中\(\lambda\)越大，每次迭代\(\theta_t(1-\alpha \frac \lambda m)\)会导致\(\theta_t\)变小的速度越快，可以看出\(\lambda\)对控制\(\theta_1 \cdots \theta_n\)绝对值大小的作用

带正则化的Logistic回归

代价函数

代价函数中的正则化项与带正则化的线性回归完全相同

\[J(\theta)=\frac 1 m \sum_{i=1}^m[-y^{(i)}log(h_\theta(X^{(i)}))-(1-y^{(i)})log(1-h_\theta(X^{(i)}))]+\frac \lambda {2m} \sum_{i=1}^n \theta_i^2 \]

梯度下降

梯度下降的公式中，新增的正则化部分与带正则化的线性回归完全相同

\[\frac{\partial J(\theta)}{\partial \theta_0}=\frac 1 m \sum_{i=1}^m\ (g(X^{(i)}\theta)-y^{(i)})x_0^{(i)}=\frac 1 m (g(X\theta)-y)^T \begin{pmatrix} x_0^{(1)}\\ \vdots\\ x_0^{(m)} \end{pmatrix}\]

\[\frac{\partial J(\theta)}{\partial \theta_t}=\frac 1 m \sum_{i=1}^m\ (g(X^{(i)}\theta)-y^{(i)})x_t^{(i)}+\frac \lambda m \theta_t \]

\[=\frac 1 m (g(X\theta)-y)^T \begin{pmatrix} x_t^{(1)}\\ \vdots\\ x_t^{(m)} \end{pmatrix}+\frac \lambda m \theta_t ,\ \ \ \ t> 1\]