软工第二次作业（数独矩阵生成）

Github项目地址：https://github.com/qiwenzhou/sudoku

解题思路描述

看完题目之后，觉得和以前做过的跳马遍历棋盘的题目很像，所以第一反应就是用回溯法，感觉并不难，反而是没有过的git 和GitHub让我觉得会多花点时间，但是应该也不难吧，我当时是这样想。
具体的解题思路，就是使用深度优先的回溯法。
如，对f()的某一次调用，如果下一个位置能放置，就递归调用自身，然后新调用的f()中，继续判断下一个位置能否放置，如果某一个位置没有可放置的下一步，此时的数独矩阵还没有完成的话，那么就退出此次f()，回溯到上一层的f()中。在不断的回溯和前进中最终得到正确的数独矩阵。
因为之前做过类似的题，印象也很深刻，所以解决问题的技术路线并没有花费多少时间，对于关键的函数也没有画流程图，我几乎是立即就开始建项目，准备打代码，但是由于题目要求代码使用C/C++/C#，而自己已经一年没有使用过了，这一年都在使用Java和Python，C语言这样的基本功反而十分生疏，思路在脑中却不知如何下手，顿时觉得十分对不起从前 的自己，<span style="color:red">今后应该不断温习以前学过的知识</span>，防止再出现这样的窘境

• C语言
• C++
• 数据结构
  翻出了以前写的跳马遍历棋盘的代码，看了一遍，对C语言也不似刚开始生疏，对解决问题心里有了底，便马上投入编代码的过程中。

---

设计实现过程

延续之前跳马的思路，程序主要分为三个函数：    

• set（） 判断该点是否满足放置的条件
• fillform（）决定下一步的动作，是继续放置，还是回溯或者输出
• printSudo() 向文件输出完整的数独矩阵
  在函数fillform()中调用set（），联合判断下一步的动作，由于是基于深度优先的思想，一旦判断到具有可走的下一步，就立即执行。实际代码如下：

bool fillFrom(int y, int val){
	int xOrd[9];
	initXOrd(xOrd);
	for (int i = 0; i<9; i++){
		int x = xOrd[i];
		//作业要求
		if (val == 7 && x == 0 && y == 0) {
			if (fillFrom(y + 1, val))//直接下一行继续填数  
				return true;
			else {
				continue;
			}
		}
		if (set(x, y, val)){
			if (y == 8)//到了最后一行  {
				if (val == 9 || fillFrom(0, val + 1))//当前填9则结束, 否则从第一行填下一个数  
					return true;
			}
			else{
				if (fillFrom(y + 1, val))//下一行继续填当前数  
					return true;
			}
			//回溯 
			reset(x, y, val);
		}
	}
	return false;
}

实际设计代码遇到的第一个问题就是将数字以怎样的顺序填入表格中，最原始的想法就是将1到9按序填入，填完一组1到9，再填入下一组1到9，但是这样的执行会导致回溯率很高，程序的性能收到严重限制。为了找到更适合的算法，我最终在[一篇新浪博客](http://blog.sina.com.cn/s/blog_a28e3dd90101e1i2.html)中收到了启发，文章通过使用分治法将相同的数字统一填入，填完全部的1之后，再填全部的2，这样有效地减少了回溯的次数，提升了系统运行的速度。
新的思路是通过按行放置的顺序，放置完所有的1，然后放置2，以此不断推算下去。这样做还有一个额外的好处就是在检查某一点放置是否符合规则时，可以省去行冲突检查的时间。

因为使用了按行放置的方法，那么为了形成多样的数独矩阵，只能在列上面做文章。现有的办法是随机生成每一个数字放置的列顺序，通过InitXord()函数实现，具体代码如下。通过生成随机数，随机打乱X的顺序，以此做到生成不同的数独矩阵。

void initXOrd(int* xOrd)//0~8随机序列  
{
	int i, k, tmp;
	for (i = 0; i<9; i++)
	{
		xOrd[i] = i;
	}
	for (i = 0; i<9; i++)
	{
		k = rand() % 9;
		tmp = xOrd[k];
		xOrd[k] = xOrd[i];
		xOrd[i] = tmp;
	}
}

解决了放置的顺序之后，就是set（）函数，这个函数的作用就是判断某一点是否可以放置，每次放置都要调用set（）函数，作用可想而知，因此这个函数也极大影响程序的性能。

在此复习一下数独的规则，简单来说就是将数字0到9填入99的表格中，并且每行里的数字不能重复，列中的数字不能重复，在9个33的九宫格里的数字也不能重复。set（）函数的作用就是检查放置的数是否违反了规则。
最简单的检查办法就是对列和小九宫格进行遍历，鉴于矩阵很小（9*9），这样的实现是具有一定可行性的，但是否有更快的方法呢？
我在本次程序中使用的方法依然基于分治法，总体的思路为：开辟一个列检查矩阵checkCol[9][9]和九宫格检查矩阵checkBox[9][9]，在列检查矩阵中，checkCol[i][j]映射为第i列的数字 j 如果checkCol[i][j]为0，表示在这一列中数字j还未存放过，也就不存在重复，可以放置，将其赋值为1；如果为1，则表示第 i 列中的数字 j 已经存在，不能继续放置数字 j 。同样的想法应用于checkBox[9][9]，将九个小九宫格编号，checkBox[i][j] 映射为第 i 个九宫格的数字 j，如果为0表示为放置，1表示已放置。这样将set（）的时间复杂度减少到n(1)。下面为set（）函数代码：

bool set(int x, int y, int val)
{
	if (sudo[y][x] != 0)//非空  
		return false;
	if (checkCol[x][val - 1] == 1)
		return false;
	int y0 = y / 3;
	int x0 = x / 3;
	int i = y0 * 3 + x0;
	if (checkBox[i][val - 1] == 1)
		return false;
	checkCol[x][val - 1] = 1;
	checkBox[i][val - 1] = 1;
	sudo[y][x] = val;
	//printSudo();
	return true;

}

另外为了满足老师作业要求中对左上角数字的固定，在初始化矩阵时将数字写入：

void init() {
	for (int i = 0; i < 9; i++) {
		for (int j = 0; j < 9; j++) {
			sudo[i][j] = 0;
			checkCol[i][j] = 0;
			checkBox[i][j] = 0;
		}
	}
	//作业要求：
	sudo[0][0] = 7;

	checkCol[0][6] = 1;
	checkBox[0][6] = 1;
}

最后一步将完成的矩阵输出到sudoku.txt中，使用

try { out.open("sudoku.txt", ios::trunc); }
	catch (exception e) {
		cout << "打开文件：sudoku.txt 失败！！";
	}

通过复写 '' << "方法，将矩阵输出到文件中。

测试运行

运行后输入要输出的矩阵的个数

结果

这是在mac pro上运行的性能分析（输出100万个矩阵）

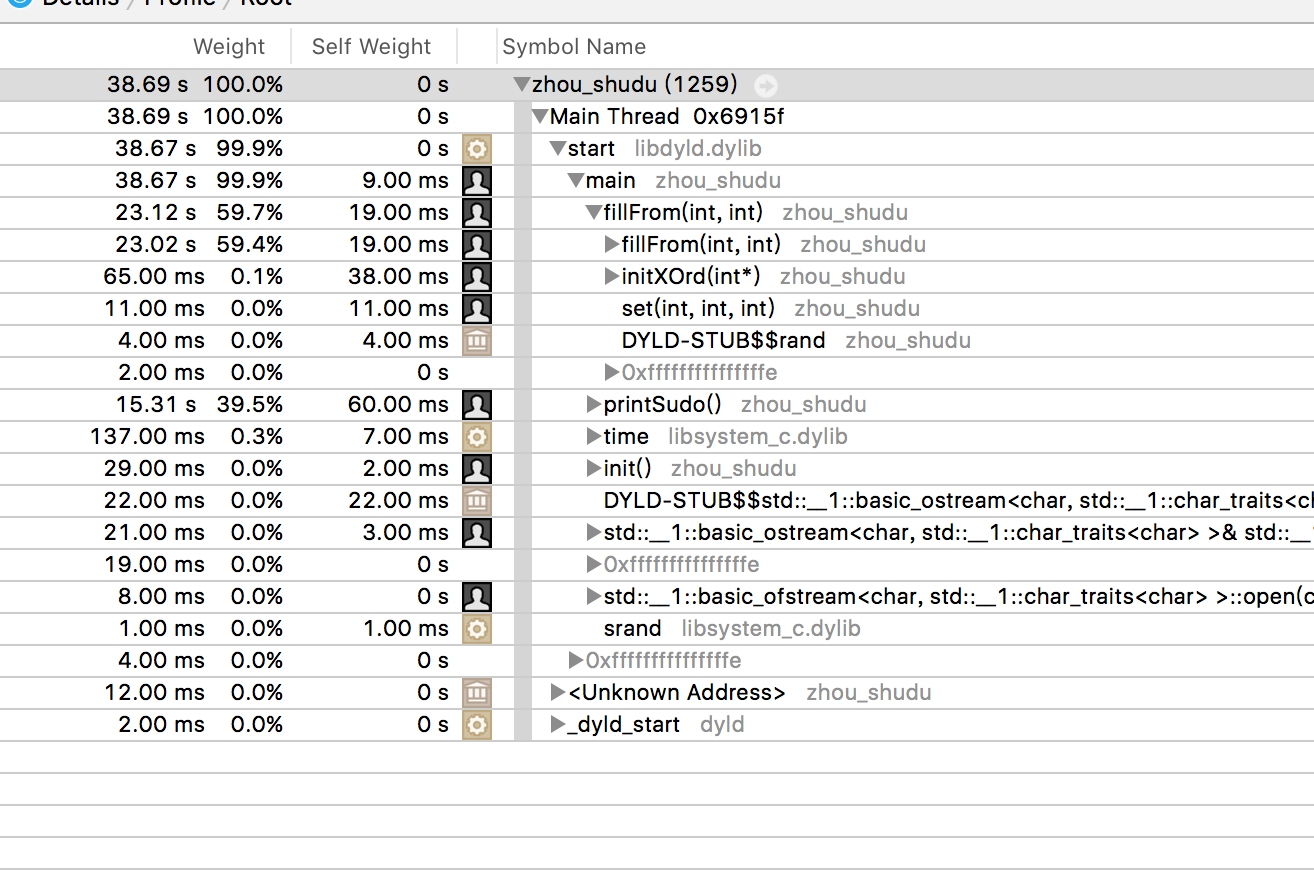
这是在自己的电脑上运行debug的性能分析（输出100万个矩阵）

运行release

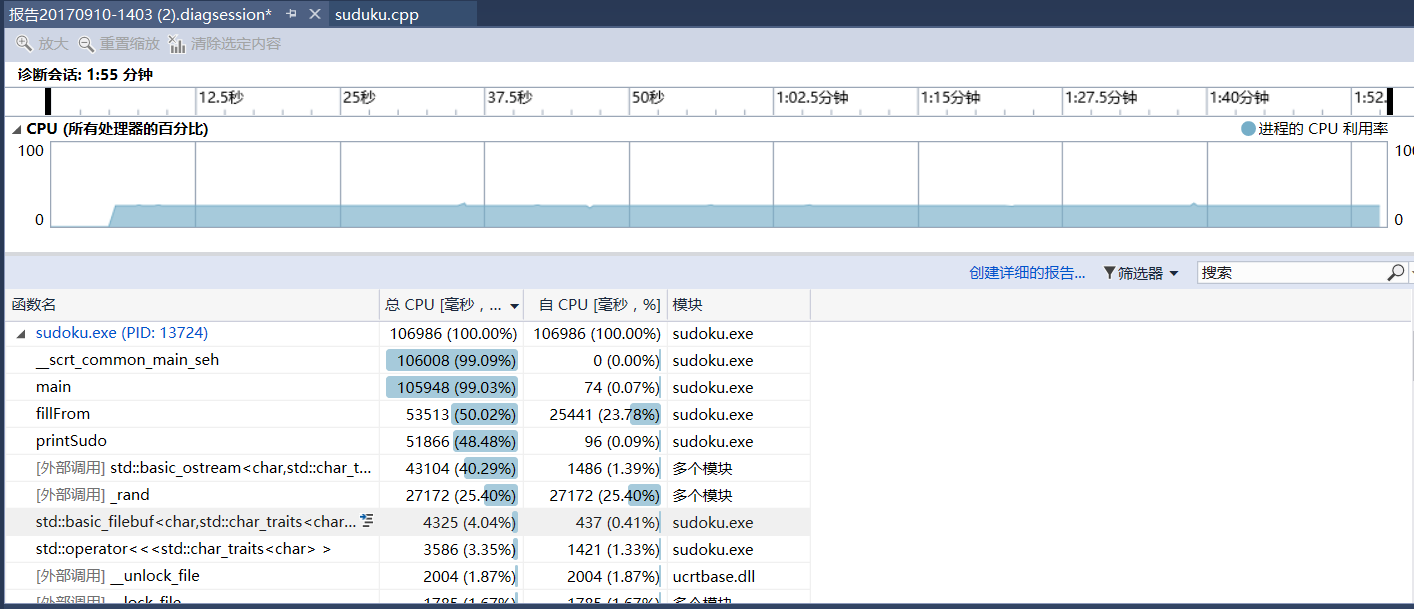
程序中消耗最大的函数为fillForm（），这并不出意外，但令我奇怪的是输出函数也占了那么大的比重，达到了近40%的比重，因为1000000次的IO太慢了，接下来思考如何加快矩阵写入文件的速度。

PSP表格记录：

PSP2.1	Personal Software Process Stages	预估耗时（分钟）	实际耗时（分钟）
Planning	计划
· Estimate	· 估计这个任务需要多少时间	8*60	10*60
Development	开发
· Analysis	· 需求分析 (包括学习新技术)	1*60	3*60
· Design Spec	· 生成设计文档	30	30
· Design Review	· 设计复审 (和同事审核设计文档)	5	5
· Coding Standard	· 代码规范 (为目前的开发制定合适的规范)	5	10
· Design	· 具体设计	0	0
· Coding	· 具体编码	1.5*60	1.5*60
· Code Review	· 代码复审	30	10
· Test	· 测试（自我测试，修改代码，提交修改）	30	2*60
Reporting	报告
· Test Report	· 测试报告	60	2*60
· Size Measurement	· 计算工作量	10	5
· Postmortem & Process Improvement Plan	· 事后总结, 并提出过程改进计划	30	30
合计		330	540