最短编辑距离问题

一、问题描述

给定两个字符串A和B，要求用少的编辑操作将A转换成B，其中允许的操作有三种：

1、替换

2、插入

3、删除

注意，A[i]=B[i]表示A和B的对应位置字符已经相同，因此在这种情况下，是不需要经过任何的编辑操作的。

例如，给定字符串A和B如下：

        String strA = "sight";
        String strB = "cite";

由A->B最少需要进行4步编辑操作，分别是：

1、替换，将A中的‘s’替换为‘c’；

2、删除，将A中的‘g’删除；

3、删除，将A中的‘h’删除；

4、插入，将‘t’插入到A的末尾

至此，尽力4步编辑操作，可以将A完全抓化为B。而且这也是成本最小的（编辑次数最少）编辑方案。

二、分析

其实有了前面的DNA序列对齐问题的求解后，在求解这个编辑距离问题就很清晰。

在DNA序列对齐问题中，打分规则b和c的两种细分情况刚好对应了编辑距离问题的替换、插入、删除三种编辑操作，打分规则a则对应了不需要编辑操作（可以想象为复制操作）的情况。

最高得分的序列对齐方案也就是用需要尽量多的复制操作和尽量少的替换、插入、删除操作完成对齐任务（当然这里有一个内在的约束条件）。

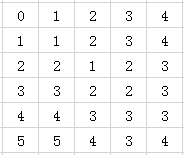
用C(i,j)表示序列A[0]...A[i]和序列B[0]...B[j]的最少编辑操作次数，其求解递推表达式为：

三、算法实现

package agdp;
public class SED {
    public static int getSED(String strA,String strB){
        int m = strA.length(),n = strB.length();
        int[][] aux = new int[m+1][n+1];//aux的第0行和第0列做哨兵，边界计算
        //边界值的初始化
        for (int i = 0; i < m+1; i++) {
            aux[i][0] = i;
        }
        for (int i = 0; i < n+1; i++) {
            aux[0][i] = i;
        }
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                if (strA.charAt(i-1) == strB.charAt(j-1)) {
                    aux[i][j] = aux[i-1][j-1];//无需编辑操作
                }else {
                    //对应替换，删除、插入中的一种，需要一次编辑擦周
                    aux[i][j] = Math.min(Math.min(aux[i-1][j], aux[i][j-1]), aux[i-1][j-1])+1;
                }
            }
        }
        return aux[m][n];
    }
    public static void main(String[] args) {
        // TODO Auto-generated method stub
        String strA = "sight";
        String strB = "cite";
//        String strA = "steal";
//        String strB = "steel";
        int count = getSED(strA, strB);
        System.out.print(count);
    }
}

其子问题的求解如下：

 参考资料：

算法导论.第十五章