钢条切割问题

一、

问题描述

给定一个长度为n英寸的钢条和一张价格表（英寸/美元），求一个切割方案使得获取的收益R最大。

例如，对于如下的价格表：

给定长度n为4英寸，则获取的最大利益为10美元，对应的切割方案为：2+2。

一种递归求解法

在不考虑切割顺序的前提下（1+(n-1)和(n-1)+1这两种切割方式实际上收益是一样的，可视为一种切割方案），长度为n的钢条共有2^(n-1)种切割方案。

可以考虑，

当被切割的子段中其中有一条为长度1的情况下，最大收益为R1；

当被切割的子段中其中有一条为长度2的情况下，最大收益为R2；

。。。

当被切割的子段中其中有一条为长度n(不做任何切割)的情况下，最大收益为Rn；

不难发现，最大收益Rmax = Max(R1,R2..Rn)；

算法实现：

    public static int getMaxReturn(int[] price,int n){
        if (n == 0) {return 0;}
        int profit = 0;
        for (int i = 1; i <= n; i++) {
            profit = Math.max(profit, price[i]+getMaxReturn(price, n-i));
        }
        return profit;
    }

该算法的实际是比较低效的，因为其递归树中求解了很多重复的子问题，未能成分利用第一次对相同子问题求解的结果。

其递归时间复杂度的递推公式为：

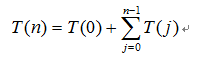
其中T(0)为递归基的调用，T(0)=1；

用错位相减：T(n)-T(n-1)可以将其化简为更加明显的递推式：

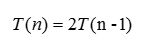
其结论已经十分明显，显然T(n)=2^n，因此该递归版本的算法是一个指数时间复杂度的算法，起根本原因在于：递归树中重复计算了很多相同子问题。子问题的规模越小，重复计算的次数就越多。

动态规划求解

分析：

从以上低效的递归算法版本优化到动态规划算法实现实际上是很自然而然的思路，既然子问题被重复计算是导致以上算法的低效的原因，那么如果能够利用对子问题求解的结果，就能避免对子问题的重复计算，优化其时间复杂度，因此会利用额外的空间存储已求得的子问题的解。

以时间换空间是动规划问题的基本特征，是典型的时空权衡的策略。

动态规划版本实现：

    public static int getMaxReturn(int[] price,int n){
        int[] aux = new int[n+1];//辅助数组，aux[0]利用
        Arrays.fill(aux, 0);
        int tmpR;
        for (int i = 1; i <= n; i++) {
            tmpR = 0;
            for (int j = 1; j <= i; j++) {
                tmpR = Math.max(tmpR, aux[i-j]+price[j]);//直接利用子问题aux[i-j]的结果，避免重复求解
            }
            aux[i] = tmpR;
        }
        return aux[n];
    }

整个过程辅助数组记录了各个子问题的最大收益：

0,1,5,8,10,13,17,18,22,25,30

二、

另外一种思考方案：

求解子问题长度为i的钢条时，由于i本身可以不切割算作一个整体，那么这里就存在一个0-1决策的问题：如果不切割，价值为p[i]；如果切割，假设在j处被切割，原问题被分成规模更小的两个子问题，前半部分的长度为j，后半部分的长度为i-j，而这两个子问题已然已经在之前求解。组合这两个子问题的最优解可以得到原问题的最优解。

切割点j是不定的，实际上由于切割的对称关系，j只需要遍历前半部分即可。

其递推式表示为：

这样思考可能不上面的动态规划在时间复杂度上争取到更小的常系数。

算法实现：

    /*
     * 动态规划版本实现，另一种实现方式
     * */
    public static int getMaxReturn(int[] price,int n){
        int[] aux = new int[n+1];//辅助数组，aux[0]不利用
        Arrays.fill(aux, 0);
        aux[1] = price[1];
        for (int i = 2; i <= n; i++) {
            for (int j = 1; j <= i/2; j++) {//由于对称性，只需要遍历i的前半部分即可
                //取C(j)+C(i-j),price[i])两者最大者，对于且与不切两种方案的最大者
                aux[i] = Math.max(aux[i], Math.max(aux[j]+aux[i-j],price[i]));
            }
        }
        return aux[n];
    }

三、

问题的升级：

给定一个长度为n(n>=2)英寸的钢条和一张价格表（英寸/美元），但是有一个限制条件：要求至少被切割一次。求一个切割方案使得获取的收益R最大。

这个问题实际上稍微不同于前面的问题，从原问题角度看必须被切割，但是其子问题可以不被切割。

因此，好的解决方案是：

要求解规模为n的原问题，先求解规模为n-1的子问题，但是求解规模为n-1的子问题是，不用管限制条件，在最有依次求解n的时候，再加上限制条件即可。

算法实现：

    /*
     * 如果钢条必须要求切割至少依次
     * */
    public static int getMaxReturn(int[] price,int n){
        int[] aux = new int[n];//辅助数组，aux[0]不利用
        Arrays.fill(aux, 0);
        for (int i = 1; i <= n-1; i++) {
            for (int j = 1; j <= i; j++) {
                aux[i] = Math.max(aux[i], aux[i-j]+price[j]);//直接利用子问题aux[i-j]的结果，避免重复求解
            }
        }
        int maxR = 0;
        for (int i = 1; i < n; i++) {
            maxR = Math.max(aux[i]+aux[n-i],maxR);
        }
        return maxR;
    }

 转载请注明原文：http://www.cnblogs.com/qcblog/p/7775366.html 

参考资料：

算法导论-第十五章