使用kd-tree加速k-means
0.目录
1.前置知识
本文内容基于《Accelerating exact k-means algorithms with geometric reasoning》
KDTree
k-means
2.思路介绍
k-means算法在初始化中心点后C通过以下迭代步骤得到局部最优解:
a.将数据集D中的点x赋给距离最近的中心点
b.在每个聚类中,重新计算中心点
传统算法中,a步需要计算n*k个距离(n为D的大小,k为聚类个数),b步需要相加n个数据点
而在KDTree中,每个非叶子节点,都存储了其包含的数据的数据范围信息h。
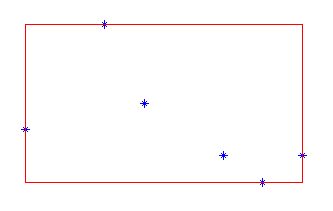 |
二维空间中的h可以使用矩形来表示 图中*为点,红色矩形为数据范围h |
a.
如果通过范围信息,能判断节点中数据都属于中心点c,则能省去节点中数据到中心点距离的计算
如果能判断h中数据都不属于某中心点c,则能省去节点中数据到中心点c距离的计算
b.
当知道节点中数据全部属于c,能将h中事先加好的统计量直接加到c的统计量中
3.详述
3.1 确定h的中心点(h中所有数据都离这个中心点近而离其他中心点远)
KDTree的节点中存储的Max(各维度上的最大值)和Min(各维度上的最小值)确定了节点中数据的范围
中心点有(c1,c2,...,ck)
a.
判断是否可能存在
计算各中心点到h的最小距离(参考KDTree最近邻查找,第5步) d(ci,h)
如果存在一个最小距离,则这个ci可能是h的中心点(还需要进一步判断)
若存在不止一个最小距离,则h的中心点不存在,需要将h分割为更小(在h的左右树上)后查找
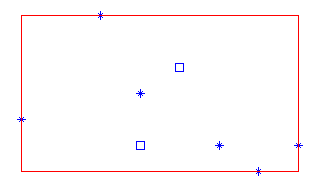 |
正方形表示的点都在h的内部 所以他们到h的最小距离相同,都为0 此h不存在中心点 |
b.
进一步判断,ci是否为中心点
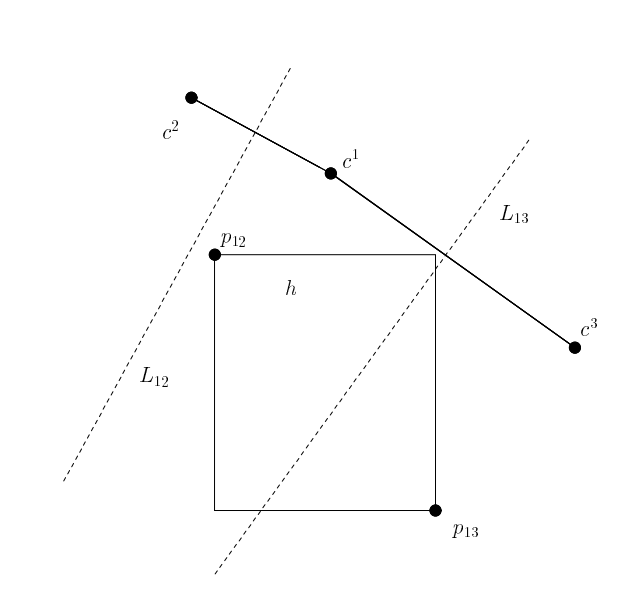 |
L12为c1和c2连线的中位线,h全部落在c1一边,
所以h中的全部点离c1比离c2近,称c1优于c2 而对于c1和c3来说,h有一部分落在c1,有一部分落在c3 c1不优于c3 |
|
判断c1是否优于c3:
取向量v=(c3-c1),找到点p属于h,使<v,p>内积最大 v各维度正负情况(+,-),则p在x轴上尽可能大,y轴上尽可能小,取到p13 p13离c3近,所以c1不优于c3 |
|
如果ci在优于其他点,则可以判定ci即为h的中心点;否则ci不是h的中心点;
虽然ci不是h的中心点,但是得到的信息,如ci优于c2,能将c2从h的子树的中心点候选列表中排除
3.2 算法步骤
|
KDTree中每个非叶子节点特殊属性: sumOfPoints:m维向量(m是数据的维度),其i维度的值为节点中数据第i维的和 n:节点中数据的个数 |
| 输入:KDTree,C 包括中心点(c1,c2,...,ck) |
| 输出:CNEW 新的k个中心点 |
| node=KDTree.root centers=k*m的数组//每行存储属于这个中心点的数据的和 datacount=k*1的数组//存储属于这个中心点的数据个数 |
|
UPDATE(node,C): IF node为叶子节点 遍历计算得到离node最近的节点ct centers[t]+=node.value; datacount[t]+=1; RETURN; FOR(ci in C) 计算d(ci,node.h) IF 有多个最小的d(ci,node.h) UPDATE(node.left,C); UPDATE(node.right,C); RETURN; //假设d(ci,node.h)最小的是ct CTOVER=[]//存储劣于ct的 FOR(ci in C(除了ct)) IF(ct 优于 ci) CTOVER.ADD(ci) IF(LEN(CTOVER)=LEN(C)-1)//ct优于其他的中心点 centers[t]+=node.sumOfPoints; datacount[t]+=node.n; RETURN; CT=(ci in C 且 ci not in CTOVER)//排除比ct差的中心点 UPDATE(node.left,CT); UPDATE(node.right,CT); RETURN; |
4.java实现
a.用下列matlab方法生成测试数据
#centers为中心点个数,dimention为数据维度,persize为每个中心点包含的数据量
function cdata(centers,dimention,persize) d=zeros(centers*persize,dimention); sigma=eye(dimention); for i=1:centers mu=randi(20,1,dimention); d(((i-1)*persize+1):i*persize,:)=mvnrnd(mu,sigma,persize); end dlmwrite('d.txt',d,'delimiter','\t','precision','%10.4f') end
b.kdtree
package cc; import java.util.ArrayList; import java.util.HashMap; public class MRKDTree { private Node mrkdtree; private class Node{ //分割的维度 int partitionDimention; //分割的值 double partitionValue; //如果为非叶子节点,该属性为空 //否则为数据 double[] value; //是否为叶子 boolean isLeaf=false; //左树 Node left; //右树 Node right; //每个维度的最小值 double[] min; //每个维度的最大值 double[] max; double[] sumOfPoints; int n; } private static class UtilZ{ /** * 计算给定维度的方差 * @param data 数据 * @param dimention 维度 * @return 方差 */ static double variance(ArrayList<double[]> data,int dimention){ double vsum = 0; double sum = 0; for(double[] d:data){ sum+=d[dimention]; vsum+=d[dimention]*d[dimention]; } int n = data.size(); return vsum/n-Math.pow(sum/n, 2); } /** * 取排序后的中间位置数值 * @param data 数据 * @param dimention 维度 * @return */ static double median(ArrayList<double[]> data,int dimention){ double[] d =new double[data.size()]; int i=0; for(double[] k:data){ d[i++]=k[dimention]; } return median(d); } private static double median(double[] a){ int n=a.length; int L = 0; int R = n - 1; int k = n / 2; int i; int j; while (L < R) { double x = a[k]; i = L; j = R; do { while (a[i] < x) i++; while (x < a[j]) j--; if (i <= j) { double t = a[i]; a[i] = a[j]; a[j] = t; i++; j--; } } while (i <= j); if (j < k) L = i; if (k < i) R = j; } return a[k]; } static double[][] maxmin(ArrayList<double[]> data,int dimentions){ double[][] mm = new double[2][dimentions]; //初始化 第一行为min,第二行为max for(int i=0;i<dimentions;i++){ mm[0][i]=mm[1][i]=data.get(0)[i]; for(int j=1;j<data.size();j++){ double[] d = data.get(j); if(d[i]<mm[0][i]){ mm[0][i]=d[i]; }else if(d[i]>mm[1][i]){ mm[1][i]=d[i]; } } } return mm; } static double distance(double[] a,double[] b){ double sum = 0; for(int i=0;i<a.length;i++){ sum+=Math.pow(a[i]-b[i], 2); } return sum; } /** * 在max和min表示的超矩形中的点和点a的最小距离 * @param a 点a * @param max 超矩形各个维度的最大值 * @param min 超矩形各个维度的最小值 * @return 超矩形中的点和点a的最小距离 */ static double mindistance(double[] a,double[] max,double[] min){ double sum = 0; for(int i=0;i<a.length;i++){ if(a[i]>max[i]) sum += Math.pow(a[i]-max[i], 2); else if (a[i]<min[i]) { sum += Math.pow(min[i]-a[i], 2); } } return sum; } public static double[] sumOfPoints(ArrayList<double[]> data, int dimentions) { double[] res = new double[dimentions]; for(double[] d:data){ for(int i=0;i<dimentions;i++){ res[i]+=d[i]; } } return res; } /** * 判断centerd是否在h上优于c * @param centerd * @param c * @param max * @param min * @return */ public static boolean isOver(double[] center, double[] c, double[] max, double[] min) { double discenter = 0; double disc = 0; for(int i=0;i<c.length;i++){ if(c[i]-center[i]>0){ disc+=Math.pow(max[i]-c[i],2); discenter+=Math.pow(max[i]-center[i],2); }else if(c[i]-center[i]<0) { disc+=Math.pow(min[i]-c[i],2); discenter+=Math.pow(min[i]-center[i],2); } } return discenter<disc; } } private MRKDTree() {} /** * 构建树 * @param input 输入 * @return KDTree树 */ public static MRKDTree build(double[][] input){ int n = input.length; int m = input[0].length; ArrayList<double[]> data =new ArrayList<double[]>(n); for(int i=0;i<n;i++){ double[] d = new double[m]; for(int j=0;j<m;j++) d[j]=input[i][j]; data.add(d); } MRKDTree tree = new MRKDTree(); tree.mrkdtree = tree.new Node(); tree.buildDetail(tree.mrkdtree, data, m,0); return tree; } /** * 循环构建树 * @param node 节点 * @param data 数据 * @param dimentions 数据的维度 */ private void buildDetail(Node node,ArrayList<double[]> data,int dimentions,int lv){ if(data.size()==1){ node.isLeaf=true; node.value=data.get(0); return; } //选择方差最大的维度 /* node.partitionDimention=-1; double var = -1; double tmpvar; for(int i=0;i<dimentions;i++){ tmpvar=UtilZ.variance(data, i); if (tmpvar>var){ var = tmpvar; node.partitionDimention = i; } } //如果方差=0,表示所有数据都相同,判定为叶子节点 if(var<1e-10){ node.isLeaf=true; node.value=data.get(0); return; } */ double[][] maxmin=UtilZ.maxmin(data, dimentions); node.min = maxmin[0]; node.max = maxmin[1]; //选取方差大的维度,会需要很长时间 //改成使用选取数据范围最大的维度 //这样构建kdtree的速度会变快,但是在kmean更新中心点会变慢 boolean isleaf = true; for(int i=0;i<node.min.length;i++) if(node.min[i]!=node.max[i]){ isleaf=false; break; } if(isleaf){ node.isLeaf=true; node.value=data.get(0); return; } node.partitionDimention=-1; double diff = -1; double tmpdiff; for(int i=0;i<dimentions;i++){ tmpdiff=node.max[i]-node.min[i]; if (tmpdiff>diff){ diff = tmpdiff; node.partitionDimention = i; } } node.sumOfPoints = UtilZ.sumOfPoints(data,dimentions); node.n = data.size(); //选择分割的值 node.partitionValue=UtilZ.median(data, node.partitionDimention); if(node.partitionValue==node.min[node.partitionDimention]){ node.partitionValue+=1e-5; } int size = (int)(data.size()*0.55); ArrayList<double[]> left = new ArrayList<double[]>(size); ArrayList<double[]> right = new ArrayList<double[]>(size); for(double[] d:data){ if (d[node.partitionDimention]<node.partitionValue) { left.add(d); }else { right.add(d); } } Node leftnode = new Node(); Node rightnode = new Node(); node.left=leftnode; node.right=rightnode; buildDetail(leftnode, left, dimentions,lv+1); buildDetail(rightnode, right, dimentions,lv+1); } public double[][] updateCentroids(double[][] cs){ int k = cs.length; int m = cs[0].length; double[][] entroids = new double[k][m]; int[] datacount = new int[k]; HashMap<Integer, double[]> cscopy = new HashMap<Integer, double[]>(); for(int i=0;i<k;i++) cscopy.put(i, cs[i]); updateCentroidsDetail(mrkdtree,cscopy,entroids,datacount,k,m); double[][] csnew = new double[k][m]; for(int i=0;i<k;i++){ for(int j=0;j<m;j++){ csnew[i][j]=entroids[i][j]/datacount[i]; } } return csnew; } private void updateCentroidsDetail(Node node, HashMap<Integer, double[]> cs, double[][] entroids, int[] datacount,int k,int m) { //如果是叶子节点 if(node.isLeaf){ double[] v=node.value; double dis=Double.MAX_VALUE; double tdis; int index = -1; //找到所属的中心点 for(Integer i: cs.keySet()){ double[] c = cs.get(i); tdis = UtilZ.distance(c, v); if(tdis<dis){ dis=tdis; index=i; } } //更新统计信息 datacount[index]++; for(int i=0;i<m;i++){ entroids[index][i]+=v[i]; } return; } double[] stack = new double[k]; int stackpoint = 0; int center=0; double tdis; for(Integer i: cs.keySet()){ double[] c = cs.get(i); tdis = UtilZ.mindistance(c, node.max, node.min); if(stackpoint==0){ stack[stackpoint++]=tdis; center=i; }else if (tdis<stack[stackpoint-1]) { stackpoint=1; stack[0]=tdis; center=i; }else if (tdis==stack[stackpoint-1]) { stack[stackpoint++]=tdis; } } //stackpoint>1,说明有多个最小值,不存在中心点 if(stackpoint!=1){ updateCentroidsDetail(node.left, cs, entroids, datacount, k, m); updateCentroidsDetail(node.right, cs, entroids, datacount, k, m); return; } HashMap<Integer, Boolean> ctover = new HashMap<Integer, Boolean>(); double[] centerd = cs.get(center); for(Integer i: cs.keySet()){ if(i==center) continue; double[] c = cs.get(i); if(UtilZ.isOver(centerd,c,node.max,node.min)){ ctover.put(i, true); } } if(ctover.size()==cs.size()-1){ //此时中心点即为center,更新信息 datacount[center]+=node.n; for(int i=0;i<m;i++){ entroids[center][i]+=node.sumOfPoints[i]; } return; } //将其比center差的中心点排除 HashMap<Integer, double[]> csnew = new HashMap<Integer, double[]>(); for(Integer i:cs.keySet()){ if(!ctover.containsKey(i)) csnew.put(i, cs.get(i)); } updateCentroidsDetail(node.left, csnew, entroids, datacount, k, m); updateCentroidsDetail(node.right, csnew, entroids, datacount, k, m); } }
c.kmeans
import cc.MRKDTree; public class KMeans { private double[][] centroids; private KMeans(){} public static class UtilZ{ static double[][] randomCentroids(double[][] data,int k){ double[][] res = new double[k][]; for(int i=0;i<k;i++){ res[i] = data[(int)(Math.random()*data.length)]; } return res; } static boolean converged(double[][] c1,double[][] c2,double c){ for(int i=0;i<c1.length;i++){ if(changed(c1[i],c2[i])>c){ return false; } } return true; } private static double changed(double[] c1,double[] c2){ double change=0; double total=0; for(int i=0;i<c1.length;i++){ total+=Math.pow(c1[i], 2); change+=Math.pow(c1[i]-c2[i], 2); } return Math.sqrt(change/total); } static double distance(double[] c1,double[] c2){ double sum = 0; for(int i=0;i<c1.length;i++){ sum+=Math.pow(c1[i]-c2[i], 2); } return sum; } } public static KMeans build(double[][] input,int k,double c,double[][] cs){ long start = System.currentTimeMillis(); MRKDTree tree = MRKDTree.build(input); System.out.println("treeConstruct:"+(System.currentTimeMillis()-start)); double[][] csnew = tree.updateCentroids(cs); while(!UtilZ.converged(cs, csnew, c)){ cs=csnew; csnew=tree.updateCentroids(cs); } KMeans km = new KMeans(); km.centroids=csnew; return km; } public static KMeans buildOri(double[][] input,int k,double c,double[][] cs){ double[][] csnew = updateOri(input,cs); while(!UtilZ.converged(cs, csnew, c)){ cs=csnew; csnew=updateOri(input,cs); } KMeans km = new KMeans(); km.centroids=csnew; return km; } private static double[][] updateOri(double[][] input,double[][] cs){ int[] center = new int[input.length]; for(int i=0;i<input.length;i++){ double dismin = Double.MAX_VALUE; for(int j=0;j<cs.length;j++){ double dis = UtilZ.distance(input[i], cs[j]); if(dis<dismin){ dismin=dis; center[i]=j; } } } double[][] nct =new double[cs.length][cs[0].length]; int[] datacount = new int[cs.length]; for(int i=0;i<input.length;i++){ double[] n = input[i]; int belong = center[i]; for(int j=0;j<cs[0].length;j++){ nct[belong][j]+=n[j]; } datacount[belong]++; } for(int i=0;i<nct.length;i++){ for(int j=0;j<nct[0].length;j++){ nct[i][j]/=datacount[i]; } } return nct; } public void printCentroids(){ java.text.DecimalFormat df=new java.text.DecimalFormat("0.00"); for(int i=0;i<centroids.length;i++){ for(int j=0;j<centroids[i].length;j++) System.out.print(df.format(centroids[i][j])+","); System.out.println(); } } }
d.调用
import java.io.BufferedReader; import java.io.FileReader; public class Test { static void compare(double[][] input){ double[][] cs = KMeans.UtilZ.randomCentroids(input, 20); int t=1; long start = System.currentTimeMillis(); while(t-->0) KMeans.build(input, 20, 0.001,cs); long kdtree = System.currentTimeMillis()-start; t=1; start = System.currentTimeMillis(); while(t-->0) KMeans.buildOri(input, 20, 0.001,cs); long ori = System.currentTimeMillis()-start; System.out.println("kdtree:"+kdtree); System.out.println("linear:"+ori); System.out.println(ori*1.0/kdtree); } public static void main(String[] args) throws Exception{ BufferedReader reader = new BufferedReader(new FileReader("d.txt")); String line=null; double[][] input = new double[600000][10]; int i=0; while((line=reader.readLine())!=null){ String[] numstrs=line.split("\t"); for(int j=0;j<10;j++) input[i][j] = Double.parseDouble(numstrs[j]); i++; } compare(input); } }
5.总结
对于数据量较小、中心点较少、维度不多的情景中,使用kd-tree并不能加速,反而比原始的算法更慢,因为kd-tree的构建花费了很长时间;
此时在选择分割维度的时候不用方差,而用数据范围,能加快kd-tree 的构建,但会下降一定的kd-tree查询性能;
当数据量大,中心点多,维度大的情况下或者在x-mean算法中,应该使用方差作为选择分割维度,此时查询性能的提升能弥补kd-tee构建的耗时



