卷积神经网络(CNN)前向传播算法
在卷积神经网络(CNN)模型结构中，我们对CNN的模型结构做了总结，这里我们就在CNN的模型基础上，看看CNN的前向传播算法是什么样子的。重点会和传统的DNN比较讨论。
1. 回顾CNN的结构
在上一篇里，我们已经讲到了CNN的结构，包括输出层，若干的卷积层+ReLU激活函数，若干的池化层，DNN全连接层，以及最后的用Softmax激活函数的输出层。这里我们用一个彩色的汽车样本的图像识别再从感官上回顾下CNN的结构。图中的CONV即为卷积层，POOL即为池化层，而FC即为DNN全连接层，包括了我们上面最后的用Softmax激活函数的输出层。
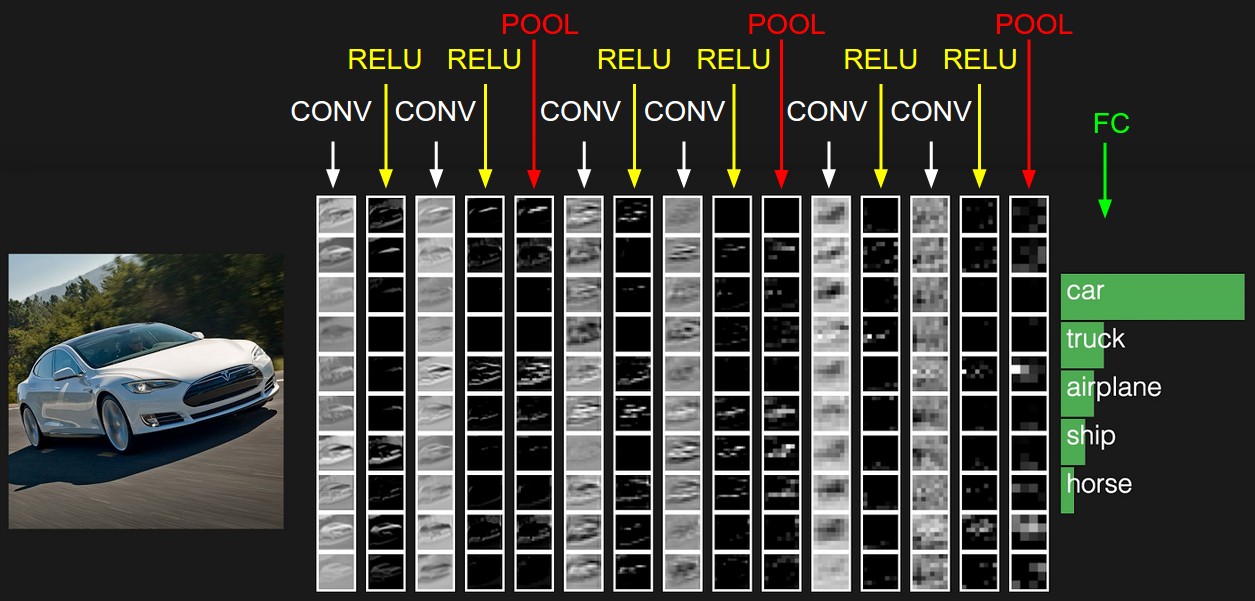
从上图可以看出，要理顺CNN的前向传播算法，重点是输入层的前向传播，卷积层的前向传播以及池化层的前向传播。而DNN全连接层和用Softmax激活函数的输出层的前向传播算法我们在讲DNN时已经讲到了。
2. CNN输入层前向传播到卷积层
输入层的前向传播是CNN前向传播算法的第一步。一般输入层对应的都是卷积层，因此我们标题是输入层前向传播到卷积层。
我们这里还是以图像识别为例。
先考虑最简单的，样本都是二维的黑白图片。这样输入层$X$就是一个矩阵，矩阵的值等于图片的各个像素位置的值。这时和卷积层相连的卷积核$W$就也是矩阵。
如果样本都是有RGB的彩色图片，这样输入$X$就是3个矩阵，即分别对应R，G和B的矩阵，或者说是一个张量。这时和卷积层相连的卷积核$W$就也是张量，对应的最后一维的维度为3.即每个卷积核都是3个子矩阵组成。
同样的方法，对于3D的彩色图片之类的样本，我们的输入$X$可以是4维，5维的张量，那么对应的卷积核$W$也是个高维的张量。
不管维度多高，对于我们的输入，前向传播的过程可以表示为：$$ a^2= \sigma(z^2) = \sigma(a^1*W^2 +b^2)$$
其中，上标代表层数，星号代表卷积，而b代表我们的偏倚, $\sigma$为激活函数，这里一般都是ReLU。
和DNN的前向传播比较一下，其实形式非常的像，只是我们这儿是张量的卷积，而不是矩阵的乘法。同时由于$W$是张量，那么同样的位置，$W$参数的个数就比DNN多很多了。
为了简化我们的描述，本文后面如果没有特殊说明，我们都默认输入是3维的张量，即用RBG可以表示的彩色图片。
这里需要我们自己定义的CNN模型参数是：
1） 一般我们的卷积核不止一个，比如有K个，那么我们输入层的输出，或者说第二层卷积层的对应的输入就K个。
2） 卷积核中每个子矩阵的的大小，一般我们都用子矩阵为方阵的卷积核，比如FxF的子矩阵。
3） 填充padding（以下简称P），我们卷积的时候，为了可以更好的识别边缘，一般都会在输入矩阵在周围加上若干圈的0再进行卷积，加多少圈则P为多少。
4） 步幅stride（以下简称S），即在卷积过程中每次移动的像素距离大小。
这些参数我们在上一篇都有讲述。
3. 隐藏层前向传播到卷积层
现在我们再来看普通隐藏层前向传播到卷积层时的前向传播算法。
假设隐藏层的输出是M个矩阵对应的三维张量，则输出到卷积层的卷积核也是M个子矩阵对应的三维张量。这时表达式和输入层的很像，也是$$ a^l= \sigma(z^l) = \sigma(a^{l-1}*W^l +b^l)$$
其中，上标代表层数，星号代表卷积，而b代表我们的偏倚, $\sigma$为激活函数，这里一般都是ReLU。
也可以写成M个子矩阵子矩阵卷积后对应位置相加的形式，即：$$ a^l= \sigma(z^l) = \sigma(\sum\limits_{k=1}^{M}z_k^l) = \sigma(\sum\limits_{k=1}^{M}a_k^{l-1}*W_k^l +b^l)$$
和上一节唯一的区别仅仅在于，这里的输入是隐藏层来的，而不是我们输入的原始图片样本形成的矩阵。
需要我们定义的CNN模型参数也和上一节一样，这里我们需要定义卷积核的个数K，卷积核子矩阵的维度F，填充大小P以及步幅S。
4. 隐藏层前向传播到池化层
池化层的处理逻辑是比较简单的，我们的目的就是对输入的矩阵进行缩小概括。比如输入的若干矩阵是NxN维的，而我们的池化大小是kxk的区域，则输出的矩阵都是$\frac{N}{k} \times \frac{N}{k}$维的。
这里需要需要我们定义的CNN模型参数是：
1）池化区域的大小k
2）池化的标准，一般是MAX或者Average。
5. 隐藏层前向传播到全连接层
由于全连接层就是普通的DNN模型结构，因此我们可以直接使用DNN的前向传播算法逻辑，即：$$a^l = \sigma(z^l) = \sigma(W^la^{l-1} + b^l)$$
这里的激活函数一般是sigmoid或者tanh。
经过了若干全连接层之后，最后的一层为Softmax输出层。此时输出层和普通的全连接层唯一的区别是，激活函数是softmax函数。
这里需要需要我们定义的CNN模型参数是：
1）全连接层的激活函数
2）全连接层各层神经元的个数
6. CNN前向传播算法小结
有了上面的基础，我们现在总结下CNN的前向传播算法。
输入：1个图片样本，CNN模型的层数L和所有隐藏层的类型，对于卷积层，要定义卷积核的大小K，卷积核子矩阵的维度F，填充大小P，步幅S。对于池化层，要定义池化区域大小k和池化标准（MAX或Average），对于全连接层，要定义全连接层的激活函数（输出层除外）和各层的神经元个数。
输出：CNN模型的输出$a^L$
1) 根据输入层的填充大小P，填充原始图片的边缘，得到输入张量$a^1$。
2）初始化所有隐藏层的参数$W,b$
3）for $l$=2 to $L-1$:
a) 如果第$l$层是卷积层,则输出为$$ a^l= ReLU(z^l) = ReLU(a^{l-1}*W^l +b^l)$$
b) 如果第$l$层是池化层,则输出为$ a^l= pool(a^{l-1})$, 这里的pool指按照池化区域大小k和池化标准将输入张量缩小的过程。
c) 如果第$l$层是全连接层,则输出为$$ a^l= \sigma(z^l) = \sigma(W^la^{l-1} +b^l)$$
4)对于输出层第L层: $$ a^L= softmax(z^L) = softmax(W^La^{L-1} +b^L)$$
以上就是CNN前向传播算法的过程总结。有了CNN前向传播算法的基础，我们后面再来理解CNN的反向传播算法就简单多了。下一篇我们来讨论CNN的反向传播算法。
（欢迎转载，转载请注明出处。欢迎沟通交流： liujianping-ok@163.com）
参考资料：
1） Neural Networks and Deep Learning by By Michael Nielsen
2） Deep Learning, book by Ian Goodfellow, Yoshua Bengio, and Aaron Courville
4）CS231n Convolutional Neural Networks for Visual Recognition, Stanford
