自用板子
最短路
打包:https://www.cnblogs.com/phemiku/p/11537316.html
快速幂和快速乘
首先,快速幂的目的就是做到快速求幂,假设我们要求a^b,按照朴素算法就是把a连乘b次,这样一来时间复杂度是O(b)也即是O(n)级别,快速幂能做到O(logn),快了好多好多。它的原理如下:
假设我们要求a^b,那么其实b是可以拆成二进制的,该二进制数第i位的权为2^(i-1),例如当b==11时 a11=a(2^0+2^1+2^3) 。
11的二进制是1011,11 = 2³×1 + 2²×0 + 2¹×1 + 2º×1,因此,我们将a¹¹转化为算 a2^0*a2^1*a2^3,也就是a1*a2*a8,看出来快的多了吧原来算11次,现在算三次,但是这三项貌似不好求的样子....不急,下面会有详细解释。 由于是二进制,很自然地想到用位运算这个强大的工具:&和>>&运算通常用于二进制取位操作,例如一个数 & 1 的结果就是取二进制的最末位。还可以判断奇偶x&1==0为偶,x&1==1为奇。>>运算比较单纯,二进制去掉最后一位。fromCXCXCXC

#include<bits/stdc++.h> using namespace std; #define int long long //这样就不用每次开long long了 const int N = 100050; inline int read() { //快读 char c = getchar(); int x = 0, f = 1; while(c < '0' || c > '9') { if(c == '-') f = -1; c = getchar(); } while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar(); return x * f; } inline int qpow(int a,int b,int mod){ //快速幂 for(int c = 1; ;a = a * a % mod){ if(b & 1)c = c * a % mod; if(!(b >>= 1))return c; } } inline int qmul(int a,int b,int mod){ //快速乘 for(int c = 0; ;a = (a << 1) % mod){ if(b & 1)c = (c + a) % mod; if(!(b >>= 1))return c; } } int n,m,a,b,q,c,d,r; signed t; signed main() { t = read(); for(int i = 1;i <= t; i++){ a = read();b = read();q = read(); c = read();d = read();r = read(); cout << qpow(a,b,q) << " "<< qmul(c,d,r) << endl ; } }
二分
跳石头地址:https://www.luogu.org/problem/P2678

#include <bits/stdc++.h> const int N = 50050; int n, d[N], m, len, ans; inline bool check(int mid) { int sum = 0, now = 0; for (int i = 1; i <= n; i++) { if (d[i] - d[now] < mid) sum++; else now = i; } if (sum > m) return 0; else return 1; } int main() { std::cin >> len >> n >> m; for (int i = 1; i <= n; i++) std::cin >> d[i]; if (!n) std::cout << len; else { int l = 1, r = len; while (l < r) { int mid = l + (r - l) / 2; if (check(mid)) { l = mid + 1; ans = mid; } else r = mid; } std::cout << ans; } return 0; }
矩阵快速幂
https://www.luogu.org/problem/P3390

#include<iostream> #include<cstring> #define mod 1000000007 #define ll long long using namespace std; struct Mat{ ll m[101][101]; }; Mat a,e; ll n,p; Mat Mul(Mat x,Mat y) //矩阵乘 { Mat c; for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) c.m[i][j]=0; for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) for(int k=1;k<=n;k++) c.m[i][j] = c.m[i][j] % mod + x.m[i][k] * y.m[k][j] % mod; return c; } Mat pow(Mat x,ll y) //矩阵快速幂 { Mat ans=e; while(y) { if(y&1) ans=Mul(ans,x); x=Mul(x,x); y>>=1; } return ans; } int main() { cin>>n>>p; for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) cin>>a.m[i][j]; for(int i=1;i<=n;i++) e.m[i][i]=1; //构造单位矩阵 Mat ans = pow(a,p); for(int i=1;i<=n;i++) { for(int j=1;j<=n;j++) cout << ans.m[i][j] % mod << " "; cout << endl; } return 0; }
堆
小根堆
https://www.luogu.org/problem/P3378

#include<iostream> #include<cstring> #include<cstdio> #include<algorithm> #include<queue> #include<vector> using namespace std; int main(){ priority_queue< int,vector<int>, greater<int> >q; int n,m,k,p,x,y; scanf("%d",&n); for(register int i = 1; i <= n; ++i){ scanf("%d",&x); if(x==1){ scanf("%d",&y); q.push(y); } else if(x==2){ printf("%d",q.top()); } else { q.pop(); } } return 0; }
高精度
高精度减法

#include<bits/stdc++.h> using namespace std; const int N= 10500; int na[N],nb[N],nc[N]; bool bj; string a,b; int main() { cin>>a>>b; if(a.size()<b.size()||(a.size()==b.size()&&a<b)){ //我果然年少又无知…string可以直接比较大小的…(ASCII码 bj=1; swap(a,b); } for(int i=a.size();i>=1;i--)na[i]=a[a.size()-i]-'0'; for(int i=b.size();i>=1;i--)nb[i]=b[b.size()-i]-'0'; int n=max(a.size(),b.size()); for(int i = 1; i <= n; i ++){ if(na[i] < nb[i]){ na[i + 1] --; na[i] += 10; } nc[i] = na[i] - nb[i]; } while(nc[n]==0)n--; if(bj)cout<<"-"; for(int i=n;i>0;i--)cout<<nc[i]; if(n<1)cout<<"0"; }
高精度乘法

#include<iostream> #include<cstring> #define maxn 100000+10 using namespace std; int na[maxn],nb[maxn],nc[maxn]; char a[maxn],b[maxn]; void mul() { int i,j,lena,lenb; memset(na,0,sizeof(na)); memset(nb,0,sizeof(nb)); memset(nc,0,sizeof(nc)); lena=strlen(a); lenb=strlen(b); for(i=0;i<lena;i++) na[i]=a[lena-i-1]-'0'; for(i=0;i<lenb;i++) nb[i]=b[lenb-i-1]-'0'; for(i=0;i<lena;i++) for(j=0;j<lenb;j++) nc[i+j]+=na[i]*nb[j]; int max=lena+lenb; for(i=0;i<max;i++) nc[i+1]+=nc[i]/10,nc[i]%=10; while(!nc[--max]); max++; for(i=0;i<max;i++) a[i]=nc[max-i-1]+'0'; a[max]='\0'; } int main() { while(cin>>a>>b) { mul(); puts(a); } return 0; }
欧几里得(辗转相除)
ll gcd(ll a, ll b) { return !b ? a : gcd(b, a%b); }
扩展欧几里得
青蛙的约会:https://www.luogu.org/problem/P1516
int exgcd(int a,int b,int &x,int &y){ if(b == 0){ x = 1, y = 0; return a; } int ret = exgcd(b, a%b, x, y); int tmp = x; x = y; y = tmp - a/b*y; return ret; }
扩欧用来做什么? [ 同余方程 ]
( a≡1(mod b) 的情况)

#include <cstdio> #include <algorithm> #include<iostream> #define MAXN 1005 typedef long long ll; int a, b, x, y, k; void exgcd(int a,int b){ if(!b){ x = 1; y = 0; return; } exgcd(b,a%b); k = x; x = y; y = k - a/b * y; return; } int main() { scanf("%d%d",&a,&b); exgcd(a,b); std::cout << (x + b) % b; return 0; }
左偏树
差分、前缀和
·区间修改后询问 http://oj.ipoweru.cn/problem/24200
#include <bits/stdc++.h> using namespace std; const int N = 1e6 + 9; typedef long long lld; #define fr(i,n) for(int i = 1; i <= n; i++) int n, m, q, l, r, od; lld a[N], d[N], s[N]; int main() { scanf("%d%d%d", &n, &m, &q); fr(i,n) scanf("%lld", &a[i]); fr(i,n) d[i] = a[i] - a[i - 1]; fr(i,m) { scanf("%d%d%d", &l, &r, &od); d[r + 1] -= od; d[l] += od; } fr(i,n) a[i] = a[i - 1] + d[i]; fr(i,n) s[i] = s[i - 1] + a[i]; fr(i,q) { scanf("%d%d", &l, &r); printf("%lld\n", s[r] - s[l - 1]); } return 0; }
线段树
https://www.luogu.org/problem/P3372

#include<bits/stdc++.h> using namespace std; const int N = 2e5 + 5; typedef long long ll; int n,m; ll sum[N << 2],tag[N << 2]; //传上去(用儿子更新自己 ) void pushup(int u) { sum[u] = sum[u << 1] + sum[u << 1 | 1]; } void buildTree(int u, int uL, int uR) { if(uL == uR) { scanf("%lld",&sum[u]); return ; } int mid = (uL + uR) >> 1; buildTree(u << 1, uL,mid); buildTree(u << 1 | 1, mid + 1,uR); pushup(u); } void update(int u, int uL, int uR, int mx) { sum[u] += (ll)(uR - uL + 1) * mx; tag[u] += mx; //lazy tag储存的是每个叶节点的修改量,不是所有 } void pushdown(int u, int uL, int uR) { if(tag[u]){ int mid = (uL + uR) >> 1; update(u << 1, uL, mid, tag[u]); update(u << 1|1, mid + 1,uR, tag[u]); tag[u] = 0; //!!记得清空 } } void modify(int u, int uL, int uR, int mL, int mR, int mx) { if(mL <= uL && mR >= uR) {//完全覆盖 update(u,uL,uR,mx); return; } //暴 躁 y z 在 线 画 图 pushdown(u,uL,uR); int mid = (uL + uR) >> 1; if(mL <= mid) modify(u << 1, uL, mid, mL, mR, mx); if(mid < mR) modify(u << 1 | 1, mid + 1, uR, mL,mR, mx); //"更新结束后传回答案" pushup(u); } ll query(int u, int uL, int uR, int mL, int mR) { if(mL <= uL && mR >= uR) return sum[u]; pushdown(u, uL, uR); int mid = (uL + uR) >> 1; ll ans = 0; if(mL <= mid) ans += query(u << 1, uL, mid, mL, mR); if(mid < mR) ans += query(u << 1 | 1, mid + 1, uR, mL, mR); return ans; } int main() { scanf("%d%d",&n,&m); buildTree(1,1,n); while(m--){ int opt,l,r,x; scanf("%d%d%d",&opt,&l,&r); if(opt == 1){ scanf("%d",&x); modify(1,1,n,l,r,x); //添加操作 } else printf("%lld\n",query(1,1,n,l,r)); // 询问操作 } return 0; }

#include <bits/stdc++.h> using namespace std; typedef long long lld; const int N = 2e5 + 9; int n, m; // sum存区间和(该线段树维护的内容),tag是懒惰标记,注意空间开4倍 lld sum[N << 2], tag[N << 2]; // 从子节点更新当前节点维护的内容,因为是维护区间和,所以直接取子节点的值相加 // 也就是把左右儿子加给他自己 void pushup(int u) { sum[u] = sum[u << 1] + sum[u << 1 | 1]; } void buildTree(int u, int uL, int uR) { if (uL == uR) { // 如果这个节点为叶结点,处理完后应当直接返回,否则递归两个子节点 scanf("%lld", &sum[u]); // 也可以先读入到另一个数组a里,这里改写为 sum[u]=a[l]; 也是对的 return; } int mid = uL + uR >> 1; // mid计算的是区间中点,以便得到子节点的区间范围 buildTree(u << 1, uL, mid); buildTree(u << 1 | 1, mid + 1, uR); // 注意要mid+1,这样区间才不会重叠 pushup(u); } // 更新当前节点维护的内容 void update(int u, int uL, int uR, int mx) { sum[u] += (lld)(uR - uL + 1) * mx; // 区间统一+mx,因此这个节点的区间和应该再乘以它对应的区间长度 // 要注意这里的类型强转,如果不转这个中间结果可能爆int tag[u] += mx; // 懒惰标记不必再乘 } // 下传Lazy Tag void pushdown(int u, int uL, int uR) { if (tag[u]) { // 如果tag值为0就不必传 int mid = uL + uR >> 1; update(u << 1, uL, mid, tag[u]); update(u << 1 | 1, mid + 1, uR, tag[u]); tag[u] = 0; // 注意传过以后tag就归零了 } } // mL与mR是操作区间范围,mx是操作参数 void modify(int u, int uL, int uR, int mL, int mR, int mx) { // 如果这个节点的区间被完全覆盖,那么直接更新它即可 if (mL <= uL && uR <= mR) { update(u, uL, uR, mx); return; } // 否则要去更新它的子节点,更新之前先下传Lazy Tag pushdown(u, uL, uR); // 具体地看是否要更新左子节点和右子节点(有可能均要更新) int mid = uL + uR >> 1; if (mL <= mid) modify(u << 1, uL, mid, mL, mR, mx); if (mid < mR) modify(u << 1 | 1, mid + 1, uR, mL, mR, mx); // 更新结束后,再从子节点回传答案 pushup(u); } lld query(int u, int uL, int uR, int mL, int mR) { // 如果这个节点的区间被完全覆盖,那么直接返回它存储的区间和即可 if (mL <= uL && uR <= mR) return sum[u]; // 否则去看它的子节点,先下传Lazy Tag pushdown(u, uL, uR); // 具体地看询问是否要用到左子节点或右子节点(如果用不到就不会访问) int mid = uL + uR >> 1; lld sum = 0; // 因为是求区间和,所以这里对应的是求和操作 if (mL <= mid) sum += query(u << 1, uL, mid, mL, mR); if (mid < mR) sum += query(u << 1 | 1, mid + 1, uR, mL, mR); return sum; } int main() { scanf("%d%d", &n, &m); buildTree(1, 1, n); while (m--) { int opt, l, r, x; scanf("%d%d%d", &opt, &l, &r); if (opt == 1) { scanf("%d", &x); modify(1, 1, n, l, r, x); } else printf("%lld\n", query(1, 1, n, l, r)); } }
树状数组
//求2^k次方的值 int lowbit(int k){ return k&-k;} //求数组的和 int query(int n) { int sum=0; while(n>0){ //当n<0时结束程序 sum+=c[n]; n=n-lowbit(n); //将n的二进制表示的最后一个零删掉 } return sum; } //修改数组元素 (此为修改数组中某个数) void modify(int i,int x) { while(i<=n){ c[i]=c[i]+x; i=i+lowbit(i); } }
树状数组模板1(单点修改,区间询问)
https://www.luogu.org/problem/P3374

#include<bits/stdc++.h> using namespace std; int n,m,k,x,l,r,ord,sum,c[500050]; //求2^k次方的值 int lowbit(int k){ return k&-k;} //求数组的和 int query(int n) { int sum=0; while(n>0){ //当n<0时结束程序 sum+=c[n]; n=n-lowbit(n); //将n的二进制表示的最后一个零删掉 } return sum; } //修改数组元素 (此为修改数组中某个数) void modify(int i,int x) { while(i<=n){ c[i]=c[i]+x; i=i+lowbit(i); } } int main() { scanf("%d%d",&n,&m); for(int i = 1; i <= n; i++){ int a; scanf("%d",&a); modify(i,a); } for(int i = 1; i <= m; i++) { //ord=1,x,k ord=2,l,r scanf("%d",&ord); if(ord == 1) { scanf("%d%d",&x,&k); modify(x,k); } else { scanf("%d%d",&l,&r); cout << query(r) - query(l - 1) << endl; } } return 0; }
树状数组模板2(区间修改,单点询问)
https://www.luogu.org/problem/P3368
(直接在上一个板子的基础上改铁定T(亲测70),考虑差分来做)

#include<bits/stdc++.h> using namespace std; const int N = 500050; int c[N], a[N], d[N]; int n, m; int lowbit(int x) {return x & (-x);} void modify(int x, int y) { while(x <= n){ c[x] += y; x += lowbit(x); } } int query(int x) { int sum = 0; while(x){ sum += c[x]; x -= lowbit(x); } return sum; } int main() { scanf("%d%d",&n, &m); for(int i = 1; i <= n; i++){ scanf("%d",&a[i]); d[i] = a[i] - a[i - 1]; //差分数组 modify(i, d[i]); } int opt, x, y, k; for(int i = 1; i <= m; i++){ scanf("%d",&opt); if(opt == 1){ scanf("%d%d%d",&x, &y, &k); modify(x, k); //差分思想 modify(y + 1, -k); } else{ scanf("%d",&x); printf("%d\n", query(x)); } } return 0; }
树状数组模板3(区间修改,区间询问)
http://oj.ipoweru.cn/problem/24201#submit_code
利用了公式:
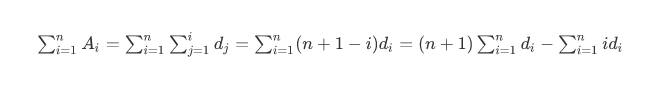

#include <cstdio> #include <cmath> #include <algorithm> using namespace std; typedef long long lld; const int N = 200005; lld a[N], d[N], id[N]; int n, m; int lowbit(int x) { return x & -x; } void modify(lld *t, int i, lld x) { while (i <= n) { t[i] += x; i += lowbit(i); } } lld query(lld *t, int i) { lld sum = 0; while (i) { sum += t[i]; i -= lowbit(i); } return sum; } lld q(int r) { return (lld)query(d, r) * (r + 1) - query(id, r); } int main() { scanf("%d%d", &n, &m); for (int i = 1; i <= n; i++) { scanf("%lld", &a[i]); modify(d, i, a[i] - a[i - 1]); modify(id, i, i * (a[i] - a[i - 1])); } while (m--) { lld opt, x, y, z; scanf("%lld %lld %lld", &opt, &x, &y); if (opt == 0) { scanf("%lld", &z); modify(d, x, z); modify(id, x, x * z); modify(d, y + 1, -z); modify(id, y + 1, (y + 1) * (-z)); } else printf("%lld\n", (lld)(q(y) - q(x - 1))); } return 0; }
归并排序

#include<bits/stdc++.h> using namespace std; #define N 1000005 int a[N] ,b[N]; long long cnt; void merge_sort(int l , int r) { if(l < r){ int mid = (l + r) / 2 ; int i = l; int p = l , q = mid+1; merge_sort(l , mid); merge_sort(mid+1 , r); while(p<=mid || q<=r){ if(q > r || (p <= mid && a[p] <= a[q])) b[i++] = a[p++]; else{ b[i++] = a[q++]; cnt += mid -p +1; //将逆序对的个数累加起来 } } for(i = l ; i <= r; i++) a[i] = b[i]; } } int main() { int n; scanf("%d",&n); for(int i = 1 ; i <= n; i ++) cin >> a[i]; cnt = 0; merge_sort(1 , n); printf("%lld",cnt); return 0; }
拓扑排序

#include<bits/stdc++.h> using namespace std; const int N = 202020; inline int read() { char c = getchar(); int x = 0, f = 1; while(c < '0' || c > '9') { if(c == '-') f = -1; c = getchar(); } while(c >= '0' && c <= '9') x = (x << 3) + (x << 1) + (c ^ 48), c = getchar(); return x * f; } int n,m,t,ind[N],a,b,len,yy[N]; vector<int>tx[N]; queue<int>q; inline bool top() { while(!q.empty()) q.pop(); //用于清空 上一组数据用的队列(第二个出错点 for(int i = 1; i <= n; i++) if(!ind[i]) q.push(i); int sum = 0; while(!q.empty()){ int u = q.front(); q.pop(); sum++; //用于统计多少数入过队 for(int i = 0; i < tx[u].size(); i++){ //第三个出错点:vector下标是从0开始 int v = tx[u][i]; ind[v]--; if(!ind[v]) q.push(v); //实现拓扑排序的关键点 } } if(sum == n) return 1; else return 0; } int main() { t = read(); for(int i = 1; i <= t; i++ ){ cin >> n >> m; memset(ind,0,sizeof(ind)); memset(tx,0,sizeof(tx)); //第一个出错点:忘记清零 for(int j = 1; j <= m; j++){ cin >> a >> b; tx[a].push_back(b); ind[b]++; } if(top()) cout << "Correct"; else cout << "Wrong"; cout << endl; } return 0; }
求组合数
·Lucas定理

#include <bits/stdc++.h> #define fr(i, n) for (register int i = 1; i <= n; i++) using namespace std; typedef long long LL; LL mod, p[200009], ans; LL qpow(LL a, LL b) { LL ans = 1; while (b) { if (b & 1) ans = (ans * a) % mod; a = (a * a) % mod; b >>= 1; } return ans; } LL lucas(LL n, LL m) { if (n < m) return 0; if (n < mod && m < mod) return qpow(p[m], mod - 2) * p[n] % mod * qpow(p[n - m], mod - 2) % mod; return lucas(n % mod, m % mod) * lucas(n / mod, m / mod) % mod; } int main() { LL n, m; int t; scanf("%d", &t); while (t--) { scanf("%lld %lld %lld", &n, &m, &mod); p[0] = 1; fr(i, mod) p[i] = p[i - 1] * i % mod; printf("%lld\n", lucas(n, m)); } }
·杨辉三角
https://www.luogu.org/problem/P2822 组合数问题90分代码

#include<iostream> #include<cstring> #include<cstdio> #define min(x,y) ((x)<(y)?(x):(y)) #define fr(i,n) for(register int i = 1; i <= n; ++i) const int N = 2005; int a[N][N],t,k,n,m; int main(){ scanf("%d%d",&t,&k); a[0][0] = 1; fr(i,2000){ a[i][0] = 1; fr(j,2000) a[i][j] = (a[i-1][j] + a[i-1][j-1]) % k; } while(t--){ int ans = 0; scanf("%d%d",&n,&m); for(int i = 0; i <= n; i++){ for(int j = 0; j <= i; j++){ if(j > m) break; if(a[i][j] % k == 0) ans++; } } printf("%d\n",ans); } return 0; onit(); }
100.乱七八糟的东西
//重载运算符比较大小
这玩意在结构体里写完了还要在下面写一个 sort( , )
struct node { int len; bool operator <(const node &a)const {//重载<操作符。可以对两个node使用<操作符进行比较 return len<a.len; } };


