递推的复习(2)
彩带
Desctiption
一中 90 周年校庆,小林准备用一些白色、蓝色和红色的彩带来装饰学校超市的橱窗,他希望满足以下两个条件:
(1) 相同颜色的彩带不能放在相邻的位置;
(2) 一条蓝色的彩带必须放在一条白色的彩带和一条红色的彩带中间。
现在,他想知道满足要求的放置彩带的方案数有多少种。
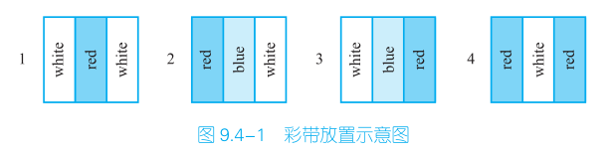
例如,如图 9.4-1 所示为橱窗宽度n=3 的所有放置方案,共 4 种。
Input
一行一个整数 n,表示橱窗宽度(或者说彩带数目)。
Output
一行一个整数,表示装饰橱窗的彩带放置方案数。
Sample Input
3
Sample Output
4
分析
这样来想,设f[n]表示宽度为n的时候有这么多种方案
1.考虑第n-1个为red or white ,此时因为不一样才可以连接着放,所以只有一种选择
2.考虑第n-1个为blue,因为要求颜色不一样才可以夹一个蓝色,所以还是只有一种选择
所以实际上就是一个斐波拉契数列,但是不同的,第一二项值都为2
Code
/*
*彩带,
*/
#include<bits/stdc++.h>
#define maxi 50
#define Int64 long long
using namespace std;
Int64 f[maxi];
int main(){
int n;
scanf("%d",&n);
f[1]=2;f[2]=2;
for(int i=3;i<=n;i++){
f[i]=f[i-1]+f[i-2];
}
printf("%d",f[n]);
return 0;
}
城市路径
Description
地图上有 n 个城市,一只奶牛要从 1 号城市开始依次经过这些城市,最终到达 n 号城市。但是这只奶牛觉得这样太无聊了,所以它决定跳过其中的一个城市(但是不能跳过 1 号和 n 号城市),使得它从 1 号城市开始,到达 n 号城市所经过的总距离最小。假设每一个城市 i 都有一个坐标(x i ,y i ),从 (x 1 ,y 1 ) 的城市 1 到 (x 2 ,y 2 ) 的城市 2 之间的距离为 | x 1 -x 2 | + | y 1 -y 2 | 。
Input
第 1 行 1 个正整数 n,表示城市个数。接下来的 n 行,每行 2 个数 x i 和 y i ,表示城市 i 的坐标
Output
第 1 行 1 个正整数 n,表示城市个数。接下来的 n 行,每行 2 个数 x i 和 y i ,表示城市 i 的坐标
Sample Input
4
0 0
8 3
11 -1
10 0
Sample Ouput
14
分析
这一个的话就是枚举跳过哪一个点省去的路程最多
我不知道这和递推有什么关系
Code
#include<bits/stdc++.h>
#define maxi 100003
#define Int64 long long
using namespace std;
Int64 f[maxi];
int n;
struct node{
int x;
int y;
}cities[maxi];
int main(){
#ifndef ONLINE_JUDGE
freopen("input.txt","r",stdin);
freopen("output.txt","w",stdout);
#endif
scanf("%d",&n);
Int64 maxcost=0,count=0;
scanf("%d%d",&cities[1].x,&cities[1].y);
for(int i=2;i<=n;++i){
scanf("%d%d",&cities[i].x,&cities[i].y);
count+=(abs(cities[i].x-cities[i-1].x)+abs(cities[i].y-cities[i-1].y));
}
for(int i=2;i<=n-1;i++){
Int64 tmp=abs(cities[i].x-cities[i-1].x)+abs(cities[i].y-cities[i-1].y);
tmp+=abs(cities[i].x-cities[i+1].x)+abs(cities[i].y-cities[i+1].y);
tmp-=abs(cities[i-1].x-cities[i+1].x)+abs(cities[i-1].y-cities[i+1].y);
maxcost=max(maxcost,tmp);
}
cout<<count-maxcost;
return 0;
}


