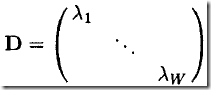在机器学习中，矩阵分析，尤其是实对称阵是经常用到的，例如：
1）Hessian Matrices：其元素是误差函数对网络权重的二阶导数
2）Convariance Matrices：高斯分布的协方差阵
对称阵的特点是
1.Eigenvector equation
对称阵的eigenvector equation
（1）
它是一系列的线性代数方程，写成矩阵形式
（2）
D是对角阵，且其对角元素正是A的特征值
（3）
公式2 有解的条件是
特征向量可经过精心选择构成正交集
2.正交化
利用矩阵U，可将矩阵A正交化
利用矩阵U，可对向量x进行变化
，且此变化有下面属性：
1）保长：
，变换前后向量长度不变
2）保角：
，变换前后向量间的夹角不变
因此通过矩阵U对向量变换，相当于对坐标系进行旋转
3.二次型
机器学习研究中经常会越到二次型函数，其中，A可以是任意矩阵，这里假定A是对称的。
利用A的正交特征矩阵U，可对上式进行分解
若A是正定的（
，v是任意非零向量），则F（X）的等高面是超椭圆，其主轴长度正比于
。
