图上随机游走问题学习笔记
听说这东西有必要学习一下?
本文内容全部参考《浅谈图模型上的随机游走问题》by 王修涵。
updated on 12.25 终于把一般图做法给学习了。
定义
给定一张有向简单图 \(G = (V,E)(V = \{v_1,v_2,\cdots,v_{|V|}\} )\)和起点 \(v_s\in V\) ,终点 \(v_t \in V\),每条边\(e = (v_x,v_y)\)有正权值\(w_e\),满足 ∀\(v_x \in V-\{v_t\},\sum_{(v_x,v_y)\in E} w(v_x,v_y) = 1\),且对于任意点 \(v_x\) 都存在一条从 \(v_x\) 出发到达 \(v_t\) 的路径。有一枚棋子从起点出发,每秒从当前所在点 \(v_x\) 以 \(w(v_x,v_y)\) 的概率选择出边 \((v_x,v_y)\) 并走向 \(v_y\) ,到达终点则停止,求期望花费时间。
思想
一般做法都是DP,根据图和题目的性质设计不同的状态来解决问题
网格图
例题(CF963E Circles of Waiting):有一枚棋子起始被放在平面直角坐标系的\((0,0)\)点。每秒棋子会随机移动。假设它当前在\((x,y)\),它下一秒有\(p_1\)的概率移动到\((x−1,y)\),\(p_2\)的概率移动到\((x,y−1)\),\(p_3\)的 概率移动到\((x+1,y)\),\(p_4\) 的概率移动到\((x,y+ 1)\)。保证 \(p_1 + p_2 + p_3 + p_4 = 1\) 。求期望 经过多少时间它会移动到一个离原点的欧几里得距离大于\(R\) 的位置。\(0≤R≤50, p_1, p_2, p_3, p_4 >0\) ,答案对\(10^9 + 7\)取模。
朴素做法
设\(f(i,j)\)表示\((i,j)\)移动到外面需要的期望时间,那么有
直接高斯消元,复杂度\(O(R^6)\)。
直接消元法
把点从左到右、从上到下标号,把方程也排个序。
考虑高斯消元的过程,发现消到\((i,j)\)时只有\((i,k),k>j\)和\((i+1,k),k\le j\)的方程有\(f(i,j)\)这个变量,所以只需要消\(O(R)\)个方程。
所以最终复杂度是\(O(R^4)\)。
主元法
把每一行第一个格子的\(f\)作为主元,从左往右推过去,得到最右边关于主元的表达式。
当欧几里得距离大于\(R\)时即可得到方程:\(f(i,j)=0\),共\(O(R)\)个方程,直接高斯消元即可。
复杂度\(O(R^3)\)。
总结
设总点数为\(n\)。
从复杂度上看,直接消元法复杂度\(O(n^2)\),主元法\(O(n\sqrt{n})\)。
精度上,据说直接消元法更优?
适用性来看:
- 网格图中存在障碍/边权为0时主元法会出现无法向右推的情况,需要再设一个主元,复杂度增加,但直接消元法复杂度不变。
- 转移方程为\(f(i,j)=p_1f(i,j+1)+p_2f(i+1,j)+p_3(pre(i,j))+1\),其中\(pre(i,j)=(x,y),x<i,y<j\)给定时直接消元法复杂度分析就是假的了,而主元法仍然可以使用。
- 求邻接矩阵行列式(别问我这东西有啥用)时只能直接消元法。
稀疏图
例题就是定义里的题,\(n,m\le 2000\),答案模随机质数。
考虑答案就是\(\sum_{t>0}P(T>t)\),可以求出走\(i\)步还没有走到终点的概率,然后求和。
设\(f_{i,u}\)表示走了\(i\)步,到了\(u\),还没有走到过终点的概率,那么有转移方程:
显然,转移方程和\(i\)无关,所以可以写成矩阵的形式:\(f_i=M\times f_{i-1}=f_0M^{i}\)。
考虑\(M\)的特征多项式\(p(\lambda)\)的次数不超过\(n\),且\(p(M)=0\),所以\(p\)就是\(M^i\)的线性递推式。
\(M^i\)左乘一个\(f_0\),线性递推式不变,所以\(f\)的线性递推式长度也不超过\(n\)。
所以\(P(T>t)=\sum_u f_{t,u}\)的递推式长度也是\(O(n)\)的,可以预处理出前\(2n\)项,然后BM算法求出递推式。设递推式的生成函数为\(C(x)\),\(a_t=P(T>t)\)的生成函数为\(A(x)\)。
那么可以得到:\(A=C\times A+A_0\),其中\(A_0\)由前\(n\)项决定。
于是可以得到\(A=\frac{A_0}{1-C}\),且易得答案就是\(x=1\)时\(A(x)\)的值,可以求出。由于模的是随机质数,可以假设分母不为0。
一般图
鸽子终于更新了。
给定一张简单强连通有向图,随机游走,对于所有起点终点求期望步数。 \(n\le 400,m\le {n(n-1)\over 2}\) 。
5.1 分析和转化
无脑设 \(p_{i,j}=[e_{i,j}\in E]{1\over deg_i}\) ,设 \(f_{i,j}\) 为答案。当 \(i\ne j\) 时有
而当 \(i=j\) 时这会算出从 \(i\) 开始走,第一次回到 \(i\) 的期望步数。设这个是 \(g_i\) ,那么有
然后写成矩阵的形式。设 \(J\) 为 \(n\) 阶全 1 矩阵, \(I\) 为 \(n\) 阶单位矩阵,那么有
如果能求出 \(G\) ,就只需要解方程
(在这里就已经可以注意到,由于 \(P\) 每一行的和是 \(1\) ,所以用 \(I\) 去减它会使得一行的和是 \(0\) ,所以把所有列向量加起来会得到零向量,即不满秩。)
5.2 \(G\) 的求法
考虑先求出一个稳态分布 \(\pi\) ,满足 \(\sum_i \pi_i=1\) ,且 \(\pi P=\pi\) 。即如果当前在每个点的概率是 \(\pi_i\) ,那么经过一步之后概率不变。
由于 \(I-P\) 不满秩,加上 \(\sum_i \pi_i=1\) 的限制后仍然可以保证能够求出 \(\pi\) 。
然后发现一个神奇的事情:对于所有 \(i\) ,有 \(\pi_ig_i=1\) 。
证明:
由于 \(G=PF+J-F\) ,两边左乘 \(\pi\) 得到 \(\pi G=\pi PF+\pi J-\pi F\) 。而 \(\pi P=\pi\) ,所以 \(\pi G=\pi J\) ,即 \(\pi_ig_i=\sum_j \pi _j =1\) 。
(有没有什么比较直觉的方法可以得到这个式子,或者得到这个思路啊?)
于是在 \(O(n^3)\) 的时间内得到的 \(G\) 。
5.3 求解原问题
前面已经说了, \(I-P\) 并不满秩,所以无法直接求解 \((I-P)F=J-G\) 。下面分析一下 \(I-P\) 的性质。
其实也没有什么好分析的。给 \(I-P\) 的第 \(i\) 行乘上 \(deg_i\) (矩阵的秩不改变), 那么就直接得到了出度矩阵减邻接矩阵。由矩阵树定理可知,这个矩阵删掉第 \(i\) 行第 \(i\) 列之后的行列式就是以 \(i\) 为根的有向生成树个数。由于图是强连通的,所以这样的树一定存在,所以删掉一行一列之后矩阵满秩。再把这行列加回来,得到 \(\text{rank} (I-P)=n-1\) 。
现在我们要解方程 \(AX=B\) ,其中 \(\text{rank}(A)=n-1\) 。 \(A,B\) 一起做高斯消元,最终可以使得 \(A\) 变成一个前 \(n-1\) 行只有主对角线为 1 、第 \(n\) 列有值,第 \(n\) 行全 0 的矩阵 \(A'\) 。
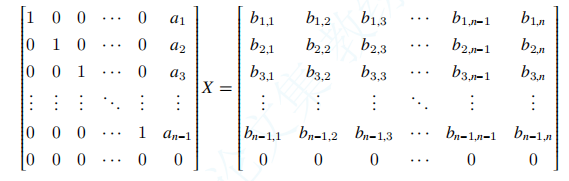
不妨先令 \(X_{n,i}=0\) ,即可得到一组特解,记为 \(Y\) 。然后需要把 \(Y\) 调整为真正的解。
我的想法
还有一个条件没有用,也就是 \(X_{i,i}=0\) 。考虑找到一个矩阵 \(Z\) ,使得 \(A'Z=0\) ,并且 \(Y+Z\) 的主对角线为 0 。
先考虑 \(A'Z=0\) 限制了什么。分开考虑 \(Z\) 的每一个列向量 \(z\) ,可以知道对于 \(i<n\) 有 \(z_i=-a_iz_n\) 。所以就是要调整每一列的 \(z_n\) ,使得 \(Z_{i,i}\) 得到想要的结果。
推一下得到 \(i\ne n\) 时 \(X_{i,j}=Y_{i,j}-Y_{j,j}/a_j\times a_i\) ,而 \(X_{n,j}=Y_{j,j}/a_j\) 。
但是论文不是这么写的。
原论文
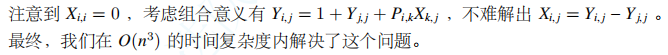
我直接懵逼……不知道为什么就搞出了 \(X_{i,j}=Y_{i,j}-Y_{j,j}\) 这么好看的形式。
不过事实证明确实有 \(a_i=-1\) ,可能就是有一些妙妙的巧合或者组合意义吧。
这里给出例题的代码: https://codeforces.com/gym/101981/submission/102289036


