POJ 1921 Paper Cut(计算几何の折纸问题)
Description
Still remember those games we played in our childhood? Folding and cutting paper must be among the most popular ones. Clever children will always search for something new, even when they play games like cutting paper. Now, Carol, a smart girl, asks her brother Mike to solve a puzzle. However, as always, Mike cannot find the solution, therefore he turns to you for help.
Carol's puzzle is simple to state. She folds the paper in a certain manner and then uses a knife to cut through the folded paper. What Mike needs to do is to tell how many pieces the folded paper will turn into after it is cut. To eliminate the ambiguity, we can coordinate the paper as [0, 1] * [0, 1], with the coordinates of lower left corner (0, 0). A fold is denoted by two points (x1, y1) and (x2, y2) on the folding line, with which, the direction of the line is determined by from (x1, y1) to (x2, y2). Carol will always fold the paper from left to right relative to the directed line given (see Figure-1). The cut is determined by the two points on the cut line. Please note that the points given to determine the fold or the cut are not necessarily on the paper.
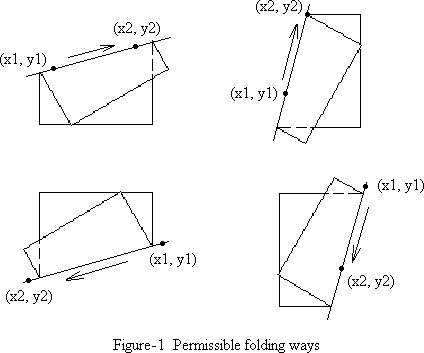
Carol's puzzle is simple to state. She folds the paper in a certain manner and then uses a knife to cut through the folded paper. What Mike needs to do is to tell how many pieces the folded paper will turn into after it is cut. To eliminate the ambiguity, we can coordinate the paper as [0, 1] * [0, 1], with the coordinates of lower left corner (0, 0). A fold is denoted by two points (x1, y1) and (x2, y2) on the folding line, with which, the direction of the line is determined by from (x1, y1) to (x2, y2). Carol will always fold the paper from left to right relative to the directed line given (see Figure-1). The cut is determined by the two points on the cut line. Please note that the points given to determine the fold or the cut are not necessarily on the paper.

Input
The first line of the input contains one integer t, the number of test cases. Then t cases follow. For each test case, the first line consists of an integer N (0 <= N <= 20), the number of folds, and the following N lines give two points on each fold line as x1, y1, x2, y2. The following line gives two points on the cut line in the same way.
Output
For each test case, output one line containing the number of pieces the paper will turn into after the cut.
题目大意:给一张正方形的纸,沿给出的n条线折叠n次,然后沿一条线切开,问切开后有多少张纸。(估计在折痕上切也可以把折痕切开)
主要是要理解上面所说的 本质不同的点。所谓本质不同的点,包括有两点虽然拥有同一个坐标,但是它们实际上是这张纸不同的点。
还有上面没有提到的,关于切割的时候,再折叠一次再切。
PS:好难……
代码(16MS):

1 #include <cstdio> 2 #include <algorithm> 3 #include <cstring> 4 #include <iostream> 5 #include <cmath> 6 #include <vector> 7 #include <map> 8 using namespace std; 9 typedef long long LL; 10 typedef pair<int, int> PII; 11 12 const double PI = acos(-1.0); 13 const double EPS = 1e-8; 14 15 inline int sgn(double x) { 16 return (x > EPS) - (x < -EPS); 17 } 18 19 struct Point { 20 double x, y; 21 Point() {} 22 Point(double x, double y): x(x), y(y) {} 23 void read() { 24 scanf("%lf%lf", &x, &y); 25 } 26 Point operator + (const Point &rhs) const { 27 return Point(x + rhs.x, y + rhs.y); 28 } 29 Point operator - (const Point &rhs) const { 30 return Point(x - rhs.x, y - rhs.y); 31 } 32 Point operator * (double t) const { 33 return Point(x * t, y * t); 34 } 35 double length() const { 36 return sqrt(x * x + y * y); 37 } 38 Point unit() const { 39 double l = length(); 40 return Point(x / l, y / l); 41 } 42 }; 43 44 double dist(const Point &p1, const Point &p2) { 45 return (p1 - p2).length(); 46 } 47 48 Point rotate(const Point &p, double angle, const Point &o = Point(0, 0)) { 49 Point t = p - o; 50 double x = t.x * cos(angle) - t.y * sin(angle); 51 double y = t.y * cos(angle) + t.x * sin(angle); 52 return Point(x, y) + o; 53 } 54 55 double cross(const Point &a, const Point &b) { 56 return a.x * b.y - a.y * b.x; 57 } 58 59 double cross(const Point &sp, const Point &ep, const Point &op) { 60 return cross(sp - op, ep - op); 61 } 62 63 struct Seg { 64 Point st, ed; 65 Seg() {} 66 Seg(Point st, Point ed): st(st), ed(ed) {} 67 void read() { 68 st.read(); ed.read(); 69 } 70 }; 71 typedef Seg Line; 72 //return Ax + By + C =0 's A, B, C 73 void Coefficient(const Line &L, double &A, double &B, double &C) { 74 A = L.ed.y - L.st.y; 75 B = L.st.x - L.ed.x; 76 C = L.ed.x * L.st.y - L.st.x * L.ed.y; 77 } 78 //point of intersection 79 Point operator * (const Line &a, const Line &b) { 80 double A1, B1, C1; 81 double A2, B2, C2; 82 Coefficient(a, A1, B1, C1); 83 Coefficient(b, A2, B2, C2); 84 Point I; 85 I.x = - (B2 * C1 - B1 * C2) / (A1 * B2 - A2 * B1); 86 I.y = (A2 * C1 - A1 * C2) / (A1 * B2 - A2 * B1); 87 return I; 88 } 89 90 double Point_to_Line(const Point &p, const Line &L) { 91 return fabs(cross(p, L.st, L.ed)/dist(L.st, L.ed)); 92 } 93 94 Point reflection(const Point &p, const Line &l) { 95 Point t = rotate(l.ed - l.st, -PI / 2); 96 return p + t.unit() * (2 * Point_to_Line(p, l)); 97 } 98 99 vector<Point> p_vec, p_buf; 100 101 struct Poly { 102 vector<int> id; 103 void add(int i) { 104 id.push_back(i); 105 } 106 Point& operator [] (int i) const { 107 return p_vec[id[i]]; 108 } 109 }; 110 111 vector<Poly> pol_vec, pol_buf; 112 map<PII, int> edge_map; 113 114 Point paper[] = {Point(0, 0), Point(0, 1), Point(1, 1), Point(1, 0)}; 115 116 void reflection(const Poly &pol, const Line &l) { 117 for(int i = 0; i < int(pol.id.size()); ++i) 118 if(pol.id[i] < int(p_buf.size())) p_buf[pol.id[i]] = reflection(pol[i], l); 119 } 120 121 int intersection(int id1, int id2, const Point &p1, const Point &p2) { 122 map<PII, int>::iterator it = edge_map.find(make_pair(id1, id2)); 123 if(it == edge_map.end()) { 124 p_vec.push_back(Line(p_vec[id1], p_vec[id2]) * Line(p1, p2)); 125 edge_map[make_pair(id1, id2)] = edge_map[make_pair(id1, id2)] = p_vec.size() - 1; 126 return p_vec.size() - 1; 127 } else return it->second; 128 } 129 130 void fold(const Point &p1, const Point &p2, const Poly &pol) { 131 Poly res1, res2; 132 int last_s = sgn(cross(p1, pol[0], p2)); 133 for(int i = 1; i < int(pol.id.size()); ++i) { 134 int now_s = sgn(cross(p1, pol[i], p2)); 135 if(now_s == 0) { 136 res1.add(pol.id[i]); 137 res2.add(pol.id[i]); 138 } else if(now_s < 0) { 139 if(last_s > 0) { 140 int k = intersection(pol.id[i - 1], pol.id[i], p1, p2); 141 res1.add(k); 142 res2.add(k); 143 } 144 res1.add(pol.id[i]); 145 } else if(now_s > 0) { 146 if(last_s < 0) { 147 int k = intersection(pol.id[i - 1], pol.id[i], p1, p2); 148 res1.add(k); 149 res2.add(k); 150 } 151 res2.add(pol.id[i]); 152 } 153 last_s = now_s; 154 } 155 if(res1.id.size() > 2) { 156 res1.add(res1.id[0]); 157 reflection(res1, Line(p1, p2)); 158 reverse(res1.id.begin(), res1.id.end()); 159 pol_buf.push_back(res1); 160 } 161 if(res2.id.size() > 2) { 162 res2.add(res2.id[0]); 163 pol_buf.push_back(res2); 164 } 165 } 166 167 void fold(const Point &p1, const Point &p2) { 168 p_buf = p_vec; 169 edge_map.clear(); 170 pol_buf.clear(); 171 for(int i = 0; i < int(pol_vec.size()); ++i) 172 fold(p1, p2, pol_vec[i]); 173 pol_vec = pol_buf; 174 for(int i = 0; i < int(p_buf.size()); ++i) 175 p_vec[i] = p_buf[i]; 176 } 177 178 void dfs(vector<bool> &vis, int id, const Line &l) { 179 vis[id] = true; 180 Poly &pol = pol_vec[id]; 181 for(int i = 0; i < int(pol.id.size() - 1); ++i) { 182 if(sgn(cross(l.ed, pol[i], l.st)) == 0 && sgn(cross(l.ed, pol[i + 1], l.st)) == 0) continue; 183 int id1 = pol.id[i], id2 = pol.id[i + 1]; 184 for(int j = 0; j < int(pol_vec.size()); ++j) { 185 if(vis[j]) continue; 186 for(int k = 0; k < int(pol_vec[j].id.size() - 1); ++k) { 187 if(pol_vec[j].id[k] == id1 && pol_vec[j].id[k + 1] == id2) { 188 dfs(vis, j, l); 189 break; 190 } 191 } 192 } 193 } 194 } 195 196 int cut(const Line &l) { 197 int ret = 0; 198 vector<bool> vis(p_vec.size()); 199 for(int i = 0; i < int(pol_vec.size()); ++i) { 200 if(!vis[i]) { 201 dfs(vis, i, l); 202 ++ret; 203 } 204 } 205 return ret; 206 } 207 208 int main() { 209 int T; 210 scanf("%d", &T); 211 Poly init_pol; 212 for(int i = 0; i <= 4; ++i) init_pol.add(i & 3); 213 while(T--) { 214 int n; 215 scanf("%d", &n); 216 p_vec.clear(); 217 pol_vec.clear(); 218 for(int i = 0; i < 4; ++i) p_vec.push_back(paper[i]); 219 for(int i = 0; i <= 4; ++i) pol_vec.push_back(init_pol); 220 Point p1, p2; 221 for(int i = 0; i <= n; ++i) { 222 p1.read(), p2.read(); 223 fold(p1, p2); 224 } 225 printf("%d\n", cut(Line(p1, p2))); 226 } 227 }




