URAL 1519 Formula 1(插头DP,入门题)
Description
Background
Regardless of the fact, that Vologda could not get rights to hold the Winter Olympic games of 20**, it is well-known, that the city will conduct one of the Formula 1 events. Surely, for such an important thing a new race circuit should be built as well as hotels, restaurants, international airport - everything for Formula 1 fans, who will flood the city soon. But when all the hotels and a half of the restaurants were built, it appeared, that at the site for the future circuit a lot of gophers lived in their holes. Since we like animals very much, ecologists will never allow to build the race circuit over the holes. So now the mayor is sitting sadly in his office and looking at the map of the circuit with all the holes plotted on it.
Problem
Who will be smart enough to draw a plan of the circuit and keep the city from inevitable disgrace? Of course, only true professionals - battle-hardened programmers from the first team of local technical university!.. But our heroes were not looking for easy life and set much more difficult problem: "Certainly, our mayor will be glad, if we find how many ways of building the circuit are there!" - they said.
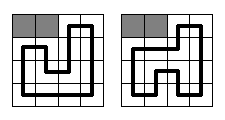
It should be said, that the circuit in Vologda is going to be rather simple. It will be a rectangle N* M cells in size with a single circuit segment built through each cell. Each segment should be parallel to one of rectangle's sides, so only right-angled bends may be on the circuit. At the picture below two samples are given for N = M = 4 (gray squares mean gopher holes, and the bold black line means the race circuit). There are no other ways to build the circuit here.
Input
The first line contains the integer numbers N and M (2 ≤ N, M ≤ 12). Each of the next N lines contains M characters, which are the corresponding cells of the rectangle. Character "." (full stop) means a cell, where a segment of the race circuit should be built, and character "*" (asterisk) - a cell, where a gopher hole is located.
Output
You should output the desired number of ways. It is guaranteed, that it does not exceed 2 63-1.
题目大意:找一个环,经过所有是'.'的点一次,问有多少个这样的哈密尔顿环。
思路:插头DP,参考IOI国家集训队论文,陈丹琦的《基于连通性状态压缩的动态规划问题》
PS:本来想不用hash的,但是写完发现状态根本存不下啊魂淡
代码(78MS):(Update:2014年11月14日)

1 #include <iostream> 2 #include <algorithm> 3 #include <cstring> 4 #include <cstdio> 5 using namespace std; 6 typedef long long LL; 7 8 const int MAXH = 20010; 9 const int SIZEH = 13131; 10 11 struct hash_map { 12 int head[SIZEH]; 13 int next[MAXH], state[MAXH]; 14 LL value[MAXH]; 15 int size; 16 17 void init() { 18 memset(head, -1, sizeof(head)); 19 size = 0; 20 } 21 22 void insert(int st, LL tv) { 23 int h = st % SIZEH; 24 for(int i = head[h]; ~i; i = next[i]) { 25 if(state[i] == st) { 26 value[i] += tv; 27 return ; 28 } 29 } 30 value[size] = tv; state[size] = st; 31 next[size] = head[h]; head[h] = size++; 32 } 33 } hashmap[2]; 34 35 hash_map *cur, *last; 36 int acc[] = {0, -1, 1, 0}; 37 38 int n, m, en, em; 39 char mat[14][14]; 40 41 int getB(int state, int i) { 42 i <<= 1; 43 return (state >> i) & 3; 44 } 45 46 int getLB(int state, int i) { 47 int ret = i, cnt = 1; 48 while(cnt) cnt += acc[getB(state, --ret)]; 49 return ret; 50 } 51 52 int getRB(int state, int i) { 53 int ret = i, cnt = -1; 54 while(cnt) cnt += acc[getB(state, ++ret)]; 55 return ret; 56 } 57 58 void setB(int &state, int i, int tv) { 59 i <<= 1; 60 state = (state & ~(3 << i)) | (tv << i); 61 } 62 63 void update(int x, int y, int state, LL tv) { 64 int left = getB(state, y); 65 int up = getB(state, y + 1); 66 if(mat[x][y] == '*') { 67 if(left == 0 && up == 0) cur->insert(state, tv); 68 return ; 69 } 70 if(left == 0 && up == 0) { 71 if(x == n - 1 || y == m - 1) return ; 72 int newState = state; 73 setB(newState, y, 1); 74 setB(newState, y + 1, 2); 75 cur->insert(newState, tv); 76 } else if(left == 0 || up == 0) { 77 if(x < n - 1) { 78 int newState = state; 79 setB(newState, y, up + left); 80 setB(newState, y + 1, 0); 81 cur->insert(newState, tv); 82 } 83 if(y < m - 1) { 84 int newState = state; 85 setB(newState, y, 0); 86 setB(newState, y + 1, up + left); 87 cur->insert(newState, tv); 88 } 89 } else { 90 int newState = state; 91 setB(newState, y, 0); 92 setB(newState, y + 1, 0); 93 if(left == 1 && up == 1) setB(newState, getRB(state, y + 1), 1); 94 if(left == 1 && up == 2 && !(x == en && y == em)) return ; 95 if(left == 2 && up == 2) setB(newState, getLB(state, y), 2); 96 cur->insert(newState, tv); 97 } 98 } 99 100 void findend() { 101 for(en = n - 1; en >= 0; --en) 102 for(em = m - 1; em >= 0; --em) if(mat[en][em] == '.') return ; 103 } 104 105 LL solve() { 106 findend(); 107 cur = hashmap, last = hashmap + 1; 108 last->init(); 109 last->insert(0, 1); 110 for(int i = 0; i < n; ++i) { 111 int sz = last->size; 112 for(int k = 0; k < sz; ++k) last->state[k] <<= 2; 113 for(int j = 0; j < m; ++j) { 114 cur->init(); 115 sz = last->size; 116 for(int k = 0; k < sz; ++k) 117 update(i, j, last->state[k], last->value[k]); 118 swap(cur, last); 119 } 120 } 121 return last->size ? last->value[0] : 0; 122 } 123 124 int main() { 125 scanf("%d%d", &n, &m); 126 for(int i = 0; i < n; ++i) scanf("%s", mat[i]); 127 cout<<solve()<<endl; 128 }




