Sequential Minimal Optimization (SMO) 算法
SVM 最终关于 $a$ 目标函数为凸优化问题,该问题具有全局最优解,许多最优化算法都可以解决该问题,但当样本容量相对很大时,通常采用 SMO 算法(比如 LIBSVM),该算法为启发式算法,考虑在约束优化问题中,目标函数的最优解 $a^*$ 是需要满足 KKT 条件的,因为对偶问题有解的充要条件就是 $a^*$ 的所有分量都满足 KKT 条件,若满足那么这时 $a^*$ 便是最优解了,否则应该找到两个分量,固定其余分量,针对这两个分量构建一个二次规划问题,目标函数关于这两个变量的解更接近原始的二次规划问题,且这时两个分量的子问题有解析解,会大大提高运算速度,两个变量的选取是首先选择违反 KKT 条件最严重的一个,另一个由约束条件确定下来,通过迭代不断选取两个分量使之满足 KKT 条件,从而使得求得原始的目标函数的最优解,这里 $a$ 每个分量 $a_i$ 均对应一个样本 $(x_i,y_i)$, 对偶问题的目标函数如下:
\begin{aligned}
&\min_a \ \ \frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N a_ia_jy_iy_j(x_i \cdot x_j) - \sum_{i=1}^Na_i \\
&s.t. \ \ \ \ \ 0 \le a_i \le C , \ i = 1,2,…,N\\
& \ \ \ \ \ \ \ \ \ \sum_{i=1}^Na_iy_i = 0,\ i = 1,2,…,N
\end{aligned}
针对选取的两个分量 $a_i,a_j$ 构建二次规划问题,使得二次规划关于这两个变量的解更接近于原始的二次规划问题,不失一般性,假设选择的两个变量为 $a_1,a_2$,固定其余分量,则最优化的子问题可以写作如下:
\begin{aligned}
&\min_{a_1,a_2} \ \ \ f(a_1,a_2) =\frac{1}{2}K_{11}a_1^2 + \frac{1}{2}K_{22}a_2^2 +y_1y_2K_{12}a_1a_2-(a_1+a_2)+y_1a_1\sum_{i=3}^Ny_ia_iK_{i1}+y_2a_2\sum_{i=3}^Ny_ia_iK_{i2} \\
&s.t. \ \ \ a_1y_1 + a_2y_2 = -\sum_{i=3}^Na_iy_i = \zeta\\
& \ \ \ \ \ \ \ \ \ 0 \le a_i \le C
\end{aligned}
这里 $K_{ij}$ 为核函数 $K(x_i,x_j)$ ,$\zeta$ 为常量,根据约束条件可以很明显看出 $a_1,a_2$ 中只要确定一个,另一个也就随之确定了,这里最后省略掉了与 $a_1,a_2$ 无关的常量。现在只需要求的满足约束条件下的新的 $a_1,a_2$ 即可,为了便于表示,用 $a_1^{old},a_2^{old}$ 表示更新前的值,$a_1^{new},a_2^{new}$ 表示更新后的值,另 $a_1^{new.unc},a_2^{new,unc}$ 为未考虑约束时的解,可以先考虑求解 $a_2^{new}$ ,然后根据 $a_2^{new}$ 与约束条件确定 $a_1^{new}$ 即可。首先为 a_2^{new} 确定一个界,即 $a_2^{new}$ 需要满足的约束,假设为 $L \le a_2^{new} \le H$ ,根据约束条件,可以得到如下的 bound :
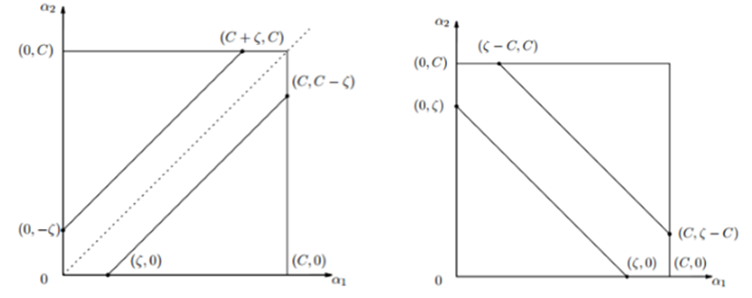
- 当 $y_1 \ne y_2$ 时,根据$a_1^{new}y_1 + a_2^{new}y_2= a_1^{old}y_1 + a_2^{old}y_2 = \zeta$ ,可得 $a_1^{old} - a_2^{old} = \zeta$, 如上图左所示当该线位于对角线以下时,$a_2^{new}$ 的最小值 $L = 0$ ,最大值为 $H = C- \zeta$ ;当该线位于对角线以上时,$a_2^{new}$ 的最小值 $L = -\zeta$ ,最大值为 $H = C$. 所以 $a_2^{new}$ 的取值范围是:
\[L = max(0,a_2^{old} – a_1^{old}) , \ \ \ \ H = min(C,C + a_2^{old} – a_1^{old})\]
- 当 $y_1 = y_2$ 时, 可得 $a_1^{old} - a_2^{old} = \zeta$ ,根据以上分析,同样可得 $a_2^{new}$ 的取值范围:
\[L = max(0,a_2^{old} + a_1^{old} -C) , \ \ \ \ H = min(C, a_2^{old} – a_1^{old})\]
确定了为了叙述简单,首先引入以下符号公式:
\begin{aligned}
g(x)&=\sum_{i=1}^{N}\alpha_iy_iK(x_i,x)+b \\
E_i &= g(x_i) – y _i= \left (\sum_{j=1}^{N}\alpha_jy_jK(x_j,x_i)+b \right ) –y_i, \ i = 1,2 \\
v_i &= \sum_{j=3}^N a_jy_jK(x_i,x_j) = g(x_i) – \sum_{j=1}^2a_jy_jK(x_i,x_j) –b , \ i = 1,2
\end{aligned}
这里 $E_i$ 为函数 $g(x)$ 对输入 $x_i$ 的预测值与真实输出 $y_i$ 的差,接下来根据约束条件 $a_1y_1 + a_2y_2 = \zeta$ ,可得 $a_1 = (\zeta – a_2y_2)y_1$ ,将 $a_1$ 与 $v_i$ 带入原优化目标:
\[\min_{a_2} = f(a_2) = \frac{1}{2}K_{11}(\zeta –a_2y_2)^2 +\frac{1}{2}K_{22}a_2^2 +y_2K_{12}(\zeta- a_2y_2)a_2 – (\zeta – a_2y_2)y_1 –a_2 + v_1(\zeta –a_2y_2) + v_2a_2y_2 \]
对 $a_2$ 求导,得到
\[\frac{\partial f}{\partial a_2} = K_{11}a_2 +K_{22}a_2 – 2K_{12}a_2 –K_{11}\zeta y_2 + K_{12}\zeta y_2 + y_1y_2 –1 – v_1y_2 +v_2y_2\]
接下来另导数为 0 求解析解即可:
\begin{aligned}
(K_{11} + K_{22} -2K_{12})a_2
&= y_2(y_2 -y_1 + \zeta K_{11} -\zeta K_{12} + v_1 – v_2) \\
&= y_2 \left [ y_2-y_1 + \zeta K_{11} -\zeta K_{12} +\left ( g(x_1) -\sum_{j=1}^2a_jy_jK_{1j}-b \right ) - \left ( g(x_2) -\sum_{i=1}^2a_jy_jK_{2j}-b \right ) \right ]
\end{aligned}
将 $\zeta = a_1^{old} y_1 + a_2^{old}y_2 $ 带入,便得到:
\begin{aligned}
(K_{11} + K_{22} -2K_{12})a_2^{new,unc}
&= y_2[(K_{11} +K_{22}-2K_{12})a_2^{old}y_2 + y_2 - y_1 +g(x_1) - g(x_2)] \\
&=(K_{11} + K_{22} - 2K_{12})a_2^{old} + y_2(E_1-E_2)
\end{aligned}
另 $\eta =K_{11} + K_{22} -2K_{12}$ ,得到无约束的解:
\[a_2^{new,unc} = a_2^{old} + \frac{y_2(E_1 –E_2)}{\eta} \tag{*}\]
最后加上之前求得的 bound ,得到了最终的 $a_2^{new}$ 的解:
\[a_2^{new} = \left\{
\begin{aligned}
&H, \ \ \ \ \ \ \ \ \ \ \ \ \ a_2^{new,unc} > H\\
&a_2^{new,unc},\ \ \ L\le a_2^{new,unc} \le H\\
&L, \ \ \ \ \ \ \ \ \ \ \ \ \ a_2^{new,unc} < L
\end{aligned} \right.\]
进一步可求得 $a_1^{new}$ 的解为:
\[ a_1^{new} = a_1^{old} + y_1y_2(a_2^{old} - a_2^{new})\]
SMO算法中的变量选择
SMO 每次迭代求解两个分量的过程中,每次选择两个变量,其中至少有一个是违反 KKT 条件的,选择第一个变量 $a_1$ 的过程叫做外层循环,外层循环选择训练样本中违反KKT条件的最严重的样本,对于样本 $(x_i,y_i)$ ,检验其是否满足 KKT 条件:
\begin{aligned}
a_i = 0 &\Leftrightarrow y_ig(x_i) \ge 1 \\
0 < a_i < C &\Leftrightarrow y_ig(x_i) = 1 \\
a_i = C &\Leftrightarrow y_ig(x_i) \le 1
\end{aligned}
这里 $g(x_i)$ 为:
\[g(x_i) = \sum_{j=1}^Na_jy_jK(x_i,x_j) + b\]
该检验的精度范围为 $\varepsilon$ ,$\varepsilon$ 为人工指定,遍历的先后顺序是首先遍历 $0 < a_i < C$ 的点,即在间隔边界上的支持向量点,如果支持向量满足 KKT 条件,接下来遍历整个训练集。
第二个变量选择的循环叫做内层循环,在选择好 $a_1$ 后 $a_2$ 的选择标准为希望 $a_2$ 有足够大的变化,根据 (*) 式可知 $a_2^{new}$ 是依赖于 $|E_1-E_2|$ 的,$a_1$ 确定了$E_1$ 也为定值,为了加快计算,可以选择使得 $|E_1 –E_2|$ 最大的 $a_2$ ,因为这时 $a_1$ 是确定的,导致 $E_1$ 也是确定的了,为了节省计算时间,可以将所有的 $E_i$ 都保存在一张表中。特殊情况下,如果 $a_2$ 使得目标函数有足够下降,则遍历间隔边界上的支持向量点,若还不行则遍历整个数据集来寻找 $a_2$ ,若此时仍无法使得目标函数有足够的下降的话,则丢弃当前的 $a_1$ ,通过外层循环重新选择一个 $a_1$ 。
优化两个变量后,需重新计算阈值 b ,当 $0 < a_1^{new} < C$ 时,由 $0 < a_i < C \Leftrightarrow y_ig(x_i) = 1$ 可知:
\[\sum_{i=1}^N a_iy_iK_{i1} + b = y_1\]
于是有:
\[b_1^{new} = y_1 – \sum_{i=3}^Na_iy_iK_{i1} - a_1^{new}y_1K_{11} –a_2^{new}y_2K_{21} \tag{a}\]
根据之前 $E_i = g(x_i) – y _i$ 的定义,可得:
\[E_1 = \sum_{i=3}^Na_iy_iK_{i1} + a_1^{old} y_1K_{11} + a_2^{old}y_2K_{21} +b^{old} – y_1\]
因此 (a) 式的前两项可改写为:
\[y_1 – \sum_{i=3}^Na_iy_iK_{i1} = –E_1 + a_1^{old}y_1K_{11} + a_2^{old} y_2 K_{21} + b^{old} \tag{b}\]
将 (b) 带入 (a) 式,可得:
\[b_1^{new} = –E_1 –y_1K_{11}(a_1^{new} – a_1^{old}) - y_2K_{21}(a_2^{new} – a_2^{old}) + b^{old}\]
当 $0< a_2^{new} <C$ 时:
\[b_2^{new} = –E_2 –y_1K_{12}(a_1^{new} – a_1^{old}) - y_2K_{22}(a_2^{new} – a_2^{old}) + b^{old}\]
如果 $a_1^{new}$ 与 $a_2 ^{new}$ 满足 $0 < a_i^{new} < C$ , 那么 $b_1^{new} = b_2^{new}$ ,如果不满足,则 $b_1^{new}$ 与 $b_2^{new}$ 之间的数都符合 KKT 条件的阈值,取他们的中点 即可,如下所示:
\[b^{new} = \left\{
\begin{aligned}
&b_1^{new} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 0 < a_1^{new} < C\\
&b_2^{new}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 0 < a_2^{new} < C\\
&(b_1^{new} + b_2^{new})/2 \ \ \ otherwise
\end{aligned} \right.\]
对应的 $E_i$ 也要做出更新,另 $S=\left\{x_j \right\}$ 为支持向量集合,
\[E_i^{new} = \sum_S a_jy_jK(x_i,x_j) + b^{new} – y_i \]
综上,最终给出完整的SMO算法。
Input: 数据集 $\left \{(x_i,y_i)\right\}_{i=1}^N$ ,精度 $\varepsilon $ ;
output:近似解 $\hat{a}$ .
(1)取初始值 $a^{(0)}=0$, 另 $k=0$ ;
(2)选取最优变量 $a_1^{(k)},a_2^{(k)}$,用两个目标变量最优化以下目标,求解最优的 $a_1^{(k+1)},a_2^{(k+1)}$, 更新 $a^{(k)}$ 为 $a^{(k+1)}$.
\begin{aligned}
&\min_{a_1,a_2} \ \ f(a_1,a_2) \\
&s.t. \ \ \ \ a_1y_1 + a_2y_2 = -\sum_{i=3}^Na_iy_i = \zeta \\
& \ \ \ \ \ \ \ \ 0 \le a_i \le C
\end{aligned}(3)若在精度 $\varepsilon$ 范围内满足停止条件.
\begin{aligned}
& \sum_{i=1}^N a_iy_i = 0 \\
& 0 \le a_i \le C, i = 1,2,…,N
\end{aligned}\[y_i \cdot g(x_i) = \left\{ \begin{aligned}
&\ge 1 \ \ \ \left \{ x_i|a_i = 0 \right \} \\
& = 1 \ \ \ \left \{ x_i| 0 < a_i < C \right \} \\
&\le 1 \ \ \ \left \{ x_i|a_i = C \right \}
\end{aligned} \right.\]其中:
\[g(x_i) = \sum_{j=1}^Na_jy_jK(x_i,x_j) +b\]
则转(4),否则 $k = k+1$ ,转(2);
(4) 得到最终结果 $\hat{a} = a^{k+1}$
参考文献