SVM 核方法
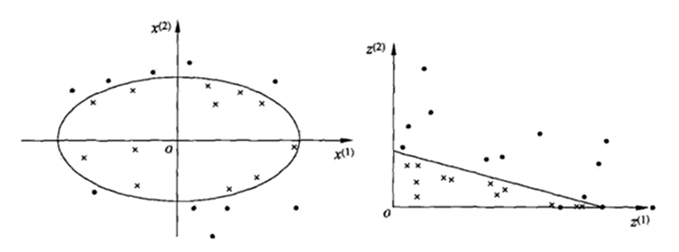
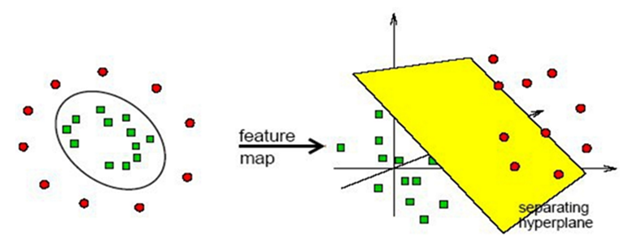
在 SVM 中引入核方法便可使得 SVM 变为非线性分类器,给定非线性可分数据集 $\left \{ (x_i,y_i)\right\}_{i=1}^N$,如下图所示,此时找不到一个分类平面来将数据分开,核方法可以将数据投影到新空间,使得投影后的数据线性可分,下图给出一个 $\mathbb{R}^2\rightarrow \mathbb{R}^2$ 的映射,原空间为 $x=(x^{(1)},x^{(2)})$ ,新空间 为 $z = \phi(x) = \left \{ (x^{(1)})^2,(x^{(2)})^2\right \}$ ,根据图可以看出映射后样本点的变化,此时样本便为线性可分的了,直接用 $w_1 \cdot z^{(1)} +w_2 \cdot z^{(2)} +b= 0$ 分类即可。
上图是一个 $\mathbb{R}^2\rightarrow \mathbb{R}^2$ 的映射,但一般情况下,特征空间的选取往往是很高维度的 $\mathbb{R}^2\rightarrow \mathbb{R}^n$ ,如下为一个 $\mathbb{R}^2\rightarrow \mathbb{R}^3$ 的映射:
下面给核函数一个正式定义,设 $\chi$ 为输入空间,$\omega$ 为特征空间,如果存在一个 $\chi$ 到 $\omega$ 的映射 $\phi(x):\chi \rightarrow \omega$ ,对所有的 $x,z \in \chi$,函数 $K(x,z)$ 满足 $K(x,z) = \phi(x)\cdot\phi(z)$ ,则称 $\phi(x)$ 为输入空间到特征空间的映射函数,$K(x,z)$ 为核函数。
核函数常用的技巧是不计算映射函数 $\phi(x)$ ,因为特征空间 $\omega$ 通常是高维的,甚至无穷维,所以 $\phi(x)$ 计算并不容易,而计算核函数 $K(x,z)$ 却相对简单。映射 $\phi(x)$ 取法多种多样,可以取不同的特征空间,即使在同一特征空间也可以取不同的映射。映射后的样本一般是线性可分带有异常值的,这时考虑 SVM 的优化目标:
\begin{aligned}
&\min_a \ \ \frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N a_ia_jy_iy_j(x_i \cdot x_j) - \sum_{i=1}^Na_i \\
&s.t. \ \ \ \ \ 0 \le a_i \le C , \ i = 1,2,…,N\\
& \ \ \ \ \ \ \ \ \ \sum_{i=1}^Na_iy_i = 0,\ i = 1,2,…,N
\end{aligned}
由于在输入空间计算的是 $x_i ,x_j$ 的内积,所以经过映射后分别为 $\phi(x_i)$ 与 $\phi(x_j)$ ,现在只需修改目标函数为 $\phi(x_i)$ 与 $\phi(x_j)$ 的内积即可,又由于 $\phi(x_i) \cdot \phi(x_j) = K(x_i,x_j)$ ,所以不需要定义映射函数 $\phi(x)$ ,只需要定义核函数便可得到高维空间中内积的结果,而这便是 Kernel Trick。所以线性不可分的数据集的优化目标变为:
\begin{aligned}
&\min_a \ \ \frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N a_ia_jy_iy_jK(x_i , x_j) - \sum_{i=1}^Na_i \\
&s.t. \ \ \ \ \ 0 \le a_i \le C , \ i = 1,2,…,N\\
& \ \ \ \ \ \ \ \ \ \sum_{i=1}^Na_iy_i = 0,\ i = 1,2,…,N
\end{aligned}
也就是说给定核函数 $K(x,z)$ ,即可用求解线性 SVM 的方法来求解非线性问题,核技巧的好处在于不需要显式的定义特征空间与映射函数,只需要选择一个合适的核函数即可。综上核函数是用来免去显式计算高维变换的,直接用低维度的参数带入核函数来等价计算高维度的向量的内积。
核函数的选择
什么样的函数 $K(x,z)$ 可以作为一个有效核函数呢?答案是只要满足 Mercer 定理 即可,即如果函数 $K(x,z)$ 是 $\mathbb{R}^n \times \mathbb{R}^n \rightarrow \mathbb{R}$ 上的映射( 也就是两个$n$ 维向量映射到实数域 )。那么如果 $K(x,z)$ 是一个有效核函数(也称为Mercer核函数),那么当且仅当其训练样本 $\left \{x_1,x_2…,x_N \right \}$ 相应的核函数矩阵是对称半正定的,这里先解释一下正定矩阵:
首先来定义奇异矩阵,若 n 阶矩阵 A 为奇异阵,则其行列式为零,即 $|A| = 0$ 。
设 M 是 n 阶方阵,如果对任何非零向量 z ,都有 $z^TMz >0$ ,其中 $z^T$ 表示 z 的转置,就称 M 为正定矩阵。
正定矩阵性质如下:
1)正定矩阵一定是非奇异的。
2)正定矩阵的任一主子矩阵也是正定矩阵。
3)若 A 为 n 阶正定矩阵,则 A 为 n 阶可逆矩阵。
对于 N 个训练样本,每一个样本 $x_i$ 对应一个训练样例。那么,我们可以将任意两个 $x_i$ 和 $x_j$ 带入核函数中,计算 $K_{ij} = K(x_i,x_j)$ 。这样可以把 $K_{ij}$ 表示为一个 $m \times m$ 的 Gram 矩阵,只要 Gram 矩阵为对称半正定的,则 K(x,z) 即为一个有效的核函数,Gram 矩阵如下:
\begin{bmatrix}
K_{11}& K_{12}& \cdots& K_{1m}& \\
K_{21}& K_{22}& \cdots& K_{2m}& \\
\vdots & \vdots& \ddots& \vdots& \\
K_{m1}& K_{m2}& \cdots& K_{mm}
\end{bmatrix}
显然对于自己定义的核函数判定是否为正定核不太容易,所以在工业生产中一般使用一些常用的核函数,下面给出几个:
1)线性核:线性核其实就是不采用非线性分类器,认为样本是线性可分的;
\[K(x,z) = x \cdot z +c\]
2)多项式核:该核函数对应的是一个 p 次多项式的分类器,这时需要额外调节的参数为 c p ;
\[K(x,z) = (x \cdot z +c)^p\]
3)高斯核:或者叫做径向基核,该核函数甚至可以将特征空间映射为无穷维,这时需要额外调节的参数为 $\delta$ ,
\[K(x,z) = exp \left ( \frac{-||x-z||^2 }{2 \delta^2}\right )\]
如果 $\delta$ 选得很大的话,高次特征上的权重实际上衰减得非常快,所以实际上(数值上近似一下)相当于一个低维的子空间;反过来,如果 $\delta$ 选得很小,则可以将任意的数据映射为线性可分,当然,这并不一定是好事,因为随之而来的可能是非常严重的过拟合问题。总的来说,通过调控参数 $\delta$ ,高斯核实际上具有相当高的灵活性,也是使用最广泛的核函数之一。
综上,给出非线性可分支持向量机的学习算法1.4:
给定非线性可分数据集 $\left \{ (x_i,y_i)\right\}_{i=1}^N$ ;
(1)构造约束最优化问题:
\begin{aligned}
&\min_a \ \ \frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N a_ia_jy_iy_jK(x_i , x_j) - \sum_{i=1}^Na_i \\
&s.t. \ \ \ \ \ 0 \le a_i \le C , \ i = 1,2,…,N\\
& \ \ \ \ \ \ \ \ \ \sum_{i=1}^Na_iy_i = 0,\ i = 1,2,…,N
\end{aligned}(2)求解得到 $a^* = (a^*_1,a^*_2,…,a^*_N)$ ,求解一般采用SMO算法
(3)根据 $a^*$ 求解得到 $w^*,b^*$ ,首先选择 $0<a_j^*<C$ ,的支持向量 $(x_j,y_j)$ :
\begin{aligned}
&w^* = \sum_{i=1}^Na_i^*y_ix_i\\
&b^* = y_j - \sum_{i=1}^N y_ia_i^*K(x_i , x_j)
\end{aligned}(4)求得超平面 $w^* \cdot x +b^* = 0$ , 对于新的观测数据 $x$ ,判断其类别:
\[f(x) = sign \left( \sum_{i=1}^N a_i^*y_iK(x,x_i) +b^*\right)\]