支持向量机SVM
关于 SVM 的博客目录链接,其中前1,2 两篇为约束优化的基础,3,4,5 三篇主要是 SVM 的建模与求解, 6 是从经验风险最小化的方式去考虑 SVM。
2. 格朗日对偶
3. 支持向量机SVM
4. SVM 核方法
Introduction
支持向量机(Support Vector Machine,SVM)是定义在特征空间中的最大间隔线性分类器,对于非线性可分的数据,SVM引入核方法(kernel trick)使它实质上成为非线性分类器。SVM 有两种解释
- 求解间隔最大的分类平面,这种情况可以转化为一个求解凸二次规划的问题,一般转换为对偶问题求解;
- Hinge Loss,通过经验风险最小化,采取 Hinge Loss 来求得损失函数,最终对损失函数求极值即可。
本文主要讲解的是二次规划转对偶求解的方式,Hinge Loss解释参考支持向量机之Hinge Loss 解释,下面步入正题,首先引入线性可分的概念。
线性可分
给定N个数据的集合 $\left \{ (x_i,y_i)\right \}_{i=1}^N $, 其中 $x_i \in \mathbb{R}^n$ 为样本点, $y_i \in \mathbb{R}$为类标签, 每个 $(x_i,y_i)$ 的组合为一个训练样例,线性可分意味着即存在一个超平面 $w \cdot x +b= 0$,可以将这两类数据分开,使得超平面一边的数据点所对应的标签 $y$ 全是+1 ,另一边对应的标签 $y$ 全为-1。需要注意,当训练数据线性可分时,存在无穷多超平面可以将两类数据正确分开,SVM 的思想是利用几何间隔最大来求解最优分类超平面,这个解是唯一的。
最大化几何间隔
一般来说,训练样本距离分类超平面的远近可以表示分类预测的确信程度,下图中点 C 的类别为 -1 确信程度要明显高于点 A 。 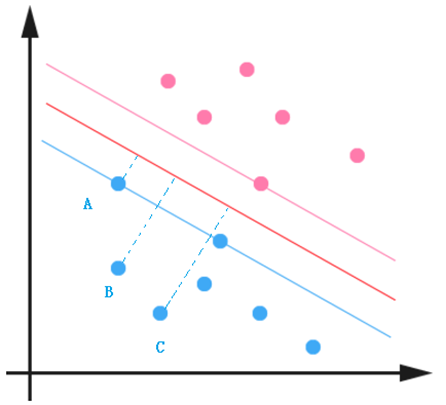
该确信程度可以用样本到超平面的距离来表示,该距离便是常说的几何距离(点到直线的距离)。样本点 $x_i$ 到分类平面 $w \cdot x_i +b= 0$ 的几何距离如下所示:
\[\gamma_i = \frac{|w \cdot x_i +b|}{||w||}\]
分子要取绝对值,分母为 $L_2$ 范数: $||w|| = \sqrt{w_1^2 + w_2^2+...+w_n^2}$,训练样例中若 $w \cdot x_i +b> 0$ ,则对应的标签为 $y_i = 1$ , 反之,若 $w \cdot x_i +b< 0$ ,则有 $y_i =-1$ ,所以将几何间隔写作如下形式:
\[\gamma_i = y_i \left (\frac{w }{||w||}x_i +\frac{b }{||w||}\right )\]
对于整个个训练集的几何距离,可表示为所有N个训练样本中的最小的几何距离:
\[ \gamma = \min_{i = 1...N} \gamma_i\]
有了训练数据的几何间隔,根据最大间隔超平面思想,可以得到以下约束最优化问题:
\begin{aligned}
&\max_{w,b}\gamma \\
&s.t. \ \ y_i\left ( \frac{w}{||w||}\cdot x_i + \frac{b}{||w||} \right ) \ge \gamma, \ \ i = 1,2,...,N
\end{aligned}
约束条件的意思是使得训练集合中所有样本的几何间隔至少要大于最小的几何间隔 $\gamma$. 这里在引入一个逻辑概念,叫做函数间隔,样本 $(x_i,y_i)$ 的函数间隔如下:
\[\gamma_i = y_i \left (w \cdot x_i+b \right )\]
进而可得整个数据集的函数间隔为:
\[\widehat{\gamma} = \min_{i=1...N} \widehat{\gamma}_i\]
与几何间隔的关系分别由以下两个公式给出:
\[\gamma_i = \frac{\widehat{\gamma}_i}{||w||}, \ \ \gamma = \frac{\widehat{\gamma} }{||w||}\]
根据以上函数间隔,可以使用函数间隔代替几何间隔来对 SVM 目标函数进一步化简:
\begin{aligned}
&\max_{w,b} \frac{\widehat{\gamma }}{||w||} \\
&s.t. \ \ y_i\left ( w\cdot x_i + b \right ) \ge \widehat{\gamma }, \ \ i = 1,2,...,N
\end{aligned}
这里之所以引入函数间隔,是因为其可以自由缩放大小的,比如对于分类超平面 $w \cdot x +b= 0$ , 若左右同时扩大 $\lambda$ 倍,$\lambda w \cdot x +\lambda b= 0$ ,分类平面不会发生任何改变,但是对于点 $x_i$ 的函数间隔为:
\[\lambda \gamma_i = y_i \lambda \left (w \cdot x_i+b \right )\]
在函数间隔也扩大了 $\lambda$ 倍的情况下,分类超平面没与几何间隔却没变,所以并不会对我们的优化函数产生一丝影响,因为优化目标是最小化几何间的,也就是说缩放分类超平面参数不会对最终的结果产生影响,所以可以令数据集的函数间隔 $\widehat{\gamma }$. 最终只需极大化:
\begin{aligned}
&\max_{w,b} \frac{ 1 }{||w||} \\
&s.t. \ \ y_i\left ( w\cdot x_i + b \right ) \ge 1, \ \ i = 1,2,...,N
\end{aligned}
以上极大不等式约束问题等价于以下极小凸二次规问题:
\begin{aligned}
&\min_{w,b} \frac{ 1 }{2}||w||^2 \\
&s.t. \ \ y_i\left ( w\cdot x_i + b \right ) \ge 1, \ \ i = 1,2,...,N
\end{aligned}
综上,提炼出线性可分情况下 SVM 的学习算法,算法1.1:
输入:线性可分数据集 $\left \{ (x_i,y_i)\right \}_{i=1}^N$ .
(1)构造约束最优化问题:
\begin{aligned}
&\min_{w,b} \frac{ 1 }{2}||w||^2 \\
&s.t. \ \ y_i\left ( w\cdot x_i + b \right ) \ge 1, \ \ i = 1,2,...,N
\end{aligned}(2)求解得到$w^*,b^*$,分类超平面即为 $w^* \cdot x+b^* = 0$
(3)对于新的观测数据 $x$ , 根据 $f(x) = sign(w^* \cdot x+b^*)$ 判断其类别 $y$ 即可.
线性可分 SVM 中到分类超平面的距离为 $\frac{1}{||w||}$,因为之前我们在不影响结果的情况下,人为设定函数间隔$\widehat{\gamma}=1$,也就是说离超平面最近的点函数间隔为 1,这些点也就是之后要提到的支持向量。
转化为对偶问题
本小节主要讲解如何求解算法1.1中的不等式约束二次规划问题,二次规划是一个凸优化问题,求解该问题需要许多最优化算法的知识,之前写过两篇文章,算是 SVM 的基础,只要这两篇搞懂,SVM 就是浮云,本节许多结论不去细说,均来自这两篇文章,有看不明白的地方可以认真读读这两篇文章:
这里将引入对偶问题来进行求解,关于对于偶问题与 KKT 条件在这里真的非常重要,而且在SVM中引入对偶的好处为:
- 对偶问题必为凸优化问题.;
- 对偶问题是原始问题的下界,当满足一定条件,两者等价;
- 引入对偶问题之后,可以自然而然的引入核函数。
现在回到之前的优化目标,也即原始问题:
\begin{aligned}
&\min_{w,b} \frac{ 1 }{2}||w||^2 \\
&s.t. \ \ – (y_i ( w\cdot x_i + b ) –1)\le 0, \ \ i = 1,2,...,N
\end{aligned}
这里把不等式约束优化写成了常见的 $g(x) \le 0$ 的形式,接下来首先构造拉格朗日函数:
\[L(w,b,a) = \frac{1}{2} ||w||^2 - \sum_{i=1}^Na_i(y_i(w \cdot x_i+b) - 1)\]
接下来需要转换为对偶问题求解,首先根据拉格朗日函数写出一个原始问题,拉格朗日函数满足如下性质:
\[ \max_{w,b}L(w,b,a) = \frac{1}{2}||w||^2\]
因为满足约束时,拉格朗日函数的第二项是为 0 的,因此 SVM 的求解的原始问题的最优解 $p^*$ 为 :
\[p^* = \min_{a_i \ge 0} \max_{w,b}L(w,b,a)\]
对偶问题及其最优解 $d^*$ 为:
\[d^* = \max_{w,b} \min_{a_i \ge 0}L(w,b,a) \]
由于对偶问题为原始问题的下界,即 $p^* \ge d^*$,而且原始问题是满足 Salter 条件,也就是说:存在 $w^*,b^*,a^*$ 分别是原始问题与对偶问题的解, 且满足:
\[p^* = d^* = L(w^*,b^*,a^*)\]
由于满足 Salter 条件(即满足强对偶),可知每对满足原始问题与对偶问题的解都满足 KKT 条件,即:
\begin{aligned}
&\nabla_wL(w^*,b^*,a^*) =w^* -\sum_{i=1}^Na_i^*y_ix_i =0 \\
&\nabla_bL(w^*,b^*,a^*) =-\sum_{i=1}^N a_i^*y_i =0 \\
&a_i^*(y_i(w^* \cdot x +b^*) -1) = 0 \\
&y_i(w^* \cdot x +b^*) -1 \ge 0 \\
&a_i \ge 0 , \ i = 1,2,...,N
\end{aligned}
这里至少存在一个 $a^*_j >0$,使得 $y_j(w \cdot x_j +b)-1 = 0$ ,这便是支持向量,然后根据 KKT 条件,可得:
\begin{aligned}
w^* &= \sum_{i=1} ^N a_i^* y_ix_i \\
b^* &= y_j - \sum_{i=1}^N a_i^* y_i(x_i \cdot x_j) \\
\end{aligned}
最后来理清思路,对于原始问题,首先构造容易求解的对偶问题,由于原始问题满足 Slater 条件,可知强对偶性成立且原始问题与对偶问题有共同的最优解,根据强对偶性可知每对原始问题与对偶问题的最优解是满足 KKT 条件的,求得对偶问题的解 $a^*$ 之后根据 KKT 条件便可得到 $w^*,b^*$, 而且对偶问题的解即为原始问题的解,要先从对偶问题下手:
\[\max_{w,b} \min_{a_i \ge 0}L(w,b,a)\]
1)min部分 :假定 $a$ 为定值,求解 $L(w,b,a)$ 关于 $w,b$ 的极小值,直接对 $w,b$ 求偏导即可:
\begin{aligned}
\frac{\partial L(w,b,a)}{\partial w} &= 0 \Rightarrow w - \sum_{i=1}^N a_iy_ix_i = 0 \\
\frac{\partial L(w,b,a)}{\partial b} &= 0 \Rightarrow - \sum_{i=1}^N a_iy_i = 0
\end{aligned}
注意上式相当于产生一个约束条件 $\sum_i a_i y_i = 0$ ,将以上结果带入 $L(w,b,a) $ 会有: 2)max部分 : $\min$ 部分得到解之后,现在求关于 $a$ 的极大即可, 即现在的待优化函数 变为:
2)max部分 : $\min$ 部分得到解之后,现在求关于 $a$ 的极大即可, 即现在的待优化函数 变为:
\begin{aligned}
&\max_{a_i \ge 0} \ -\frac{1}{2}\sum_{i=1}^N\sum_{j=1}^Na_i a_jy_iy_j (x_i \cdot x_j) + \sum _{i=1}^Na_i\\
& \ s.t. \ \ \ \sum_{i=1}^N a_iy_i = 0
\end{aligned}
现在大功告成,只要求解对偶问题得到 $a^*$ ,然后根据 KKT 条件得到 $w^* ,b^*$ ,就可以完美的解得原始问题的最优解了,经过以上几步,便得到了最终的线性可分支持向量机学习算法,算法1.2:
输入:线性可分数据集 $\left \{ (x_i,y_i) \right \}_{i=1}^N$
(1)构造约束最优化问题:
\begin{aligned}
&\max_{a_i \ge 0} \ -\frac{1}{2}\sum_{i=1}^N\sum_{j=1}^Na_i a_jy_iy_j (x_i \cdot x_j) + \sum _{i=1}^Na_i\\
& \ s.t. \ \ \ \sum_{i=1}^N a_iy_i = 0
\end{aligned}(2)求解得到 $a^*= (a^*_1,a^*_2,…,a^*_N)^T$,求解一般采用SMO算法;
(3)根据之前的KKT 条件, $a^*$ 求得 $w^*,b^*$ ,首先选择 $a^*_j > 0$ 的支持向量 $(x_j,y_j)$;
\begin{aligned}
w^* &= \sum_{i=1} ^N a_i^* y_ix_i \\
b^* &= y_j - \sum_{i=1}^N a_i^* y_i(x_i \cdot x_j) \\
\end{aligned}(4)求得超平面 $w^* \cdot x +b^* = 0$, 对于新的观测数据 $x$ , 根据 $f(x) = sign(w^* \cdot x +b^*)$ 判断其类别 $y$.
这里顺便明确给出支持向量的定义:根据KKT条件 $a_i^*(y_i(w^* \cdot x_i +b^*) -1) = 0$ :
- $a_i^* >0$ 的样本点 $(x_i,y_i)$ 即为间隔边界上的支持向量,且 $y_i(w^* \cdot x_i + b^*) -1 = 0$ ;
- 对于非支持向量,即 $y_i(w^* \cdot x_i+b^*) -1 >0$ ,一定有 $a_i = 0$.
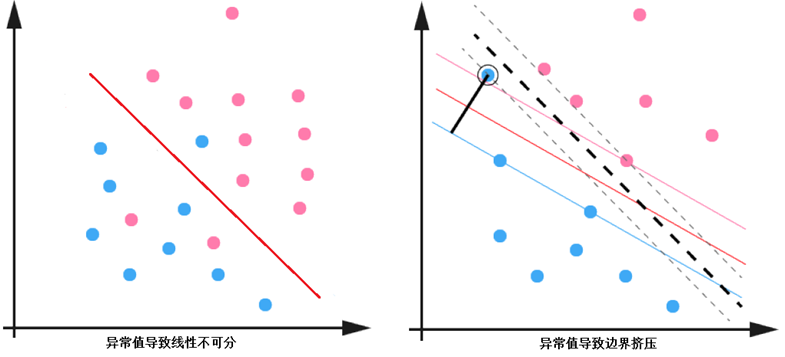
至此,关于线性可分情况下的二分类 SVM 全部推到完成,但是有一个问题:当数据中存在一些异常值(outlier),去除这些 outlier 后数据是线性可分的,这种情况下要引入关于异常值的处理。
outlier 的处理
给定数据集 $\left \{ (x_i,y_i) \right \}_{i=1}^N$ ,当样本数据大部分为线性可分的,存在少量异常值使得数据线性不可分,或者导致分离超平面被挤压,可以通过一些方法仍然按照线性可分的方式处理,异常值的情况如下图所示:
以上情况意味着某些样本点的函数间隔并不满足大于 1 的要求。为了解决这个问题,为每个样本引入一个松弛变量 $\xi _i \ge 0$ , 使得函数间隔可以小于 1 ,即满足 $y_i(w \cdot x_i +b) \ge 1 – \xi_i$ ,这里显然 $\xi _i$ 不能任意大,因为那会导致任意样本点都满足要求,所以要把优化目标改成如下的形式:
\begin{aligned}
&\min_{w,b,\xi}\ \ \frac{1}{2}||w||^2 + C\sum_{i=1}^N \xi_i \\
&s.t. \ \ \ \ -y_i(w \cdot x_i + b) -\xi_i + 1\le 0, \ \ i = 1,2,...,N \\
&\ \ \ \ \ \ \ \ \ \ -\xi_i \le 0 ,\ \ i = 1,2,...,N
\end{aligned}
这里 $C >0$ 叫做惩罚参数,上述的不等式约束记做 $g(x) \le 0$ 的形式,同样通过对偶的形式求解,首先构造拉格朗日函数:
\[L(w,b,\xi,a,\gamma) = \frac{1}{2}||w||^2 + C\sum_{i=1}^N \xi_i -\sum_{i=1}^N a_i(y_i(w \cdot x_i + b) - 1+ \xi_i) - \sum_{i=1}^N \gamma_i\xi_i\]
拉格朗日函数中的乘子 $a_i \ge 0$, 且 $\gamma_i \ge 0$ ,很明显的有:
\[ \max_{w,b,\xi}L(w,b,\xi,a,\gamma) = \frac{1}{2}||w||^2 + C\sum_{i=1}^N \xi_i\]
因此原始问题转化为:
\[ \min_{a,\gamma} \max_{w,b,\xi}L(w,b,\xi,a,\gamma) \]
对于上述问题应用对偶可得:
\[ \max_{a,\gamma} \min_{w,b,\xi} L(w,b,\xi,a,\gamma)\]
接下来求解对偶问题,对于极小部分的参数 $w,b,\xi_i$ 求导:
\begin{aligned}
&\nabla_wL(w,b,\xi,a,\gamma) = 0 \Rightarrow w - \sum_{i=1}^Na_iy_ix_i = 0 \\
&\nabla_bL(w,b,\xi,a,\gamma) = 0 \Rightarrow - \sum_{i=1}^Na_iy_i = 0 \\
&\nabla_{\xi}L(w,b,\xi,a,\gamma) = 0 \Rightarrow C - a_i -\gamma_i = 0
\end{aligned}
将以上结果带入对偶问题,极小部分便得到一个关于 $a$ 的函数:
\begin{aligned}
&\max_a \ \ -\frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N a_ia_jy_iy_j(x_i \cdot x_j) + \sum_{i=1}^Na_i \\
&s.t. \ \ \ \ \ 0 \le a_i \le C , \ i = 1,2,…,N\\
& \ \ \ \ \ \ \ \ \ \sum_{i=1}^Na_iy_i = 0,\ i = 1,2,…,N
\end{aligned}
注意这里根据 $C – a_i – \gamma_i = 0$ 与 $\gamma_i \ge 0$ 消去了 $\gamma_i$ ,同样由于原始问题满足 Slater 条件,因此存在 $w^*, b^* ,\xi_i^*$ 为原始问题的解,$\gamma^* ,a^*$ 为对偶问题的解,且强对偶条件成立,并且每对解均满足 KKT 条件:
\begin{align}
&\nabla_wL(w,b,\xi,a,\gamma) = 0 \Rightarrow w - \sum_{i=1}^Na_iy_ix_i = 0 \\
&\nabla_bL(w,b,\xi,a,\gamma) = 0 \Rightarrow - \sum_{i=1}^Na_iy_i = 0 \\
&\nabla_{\xi}L(w,b,\xi,a,\gamma) = 0 \Rightarrow C - a_i -\gamma_i = 0 \\
&a_i^* (y_i(w^* \cdot x_i + b^*) -1 + \xi_i^*) = 0\\
&y_i(w^* \cdot x_i + b^*) -1 + \xi_i^* \ge 0\\
& \gamma_i^* \xi_i^* = 0\\
&a_i^* \ge 0 \\
&\xi_i^* \ge 0\\
&\gamma_i^* \ge 0\\
\end{align}
根据 KKT 条件,求得 $a^*$ 后,便可带入求解 $w^*$ 与 $b^*$,首先由 KKT 条件 (1) 可得:
\[w^* = \sum_{i=1}^Na_i^*y_ix_i\]
根据 KKT 条件(3) (4) (6) (9)可知若 $\gamma_j^* >0$,则 $\xi_j^* = 0$ ,且存在 $0 < a_j^*< C$ ,使得:
\[y_j(w^* \cdot x_j + b^*) –1 = 0\]
因此便可求得 $b^*$ :
\[b^* = y_j – \sum_{i=1}^N y_ia_i^*(x_i \cdot x_j) \]
至此,可以总结出带有异常值的线性可分 SVM 的算法1.3:
输入:线性可分数据集 $\left \{ (x_i,y_i) \right \}_{i=1}^N$,数据集中伴有异常值
(1)构造约束最优化问题:
\begin{aligned}
&\min_a \ \ \frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N a_ia_jy_iy_j(x_i \cdot x_j) - \sum_{i=1}^Na_i \\
&s.t. \ \ \ \ \ 0 \le a_i \le C , \ i = 1,2,…,N\\
& \ \ \ \ \ \ \ \ \ \sum_{i=1}^Na_iy_i = 0,\ i = 1,2,…,N
\end{aligned}(2)求解得到 $a^* = (a^*_1,a^*_2,…,a^*_N)$ ,求解一般采用SMO算法;
(3)根据 $a^* $ 得到 $w^*,b^*$ ,选择满足 $0 < a^*_j < C$ 的分量
\begin{aligned}
&w^* = \sum_{i=1}^Na_i^*y_ix_i\\
&b^* = y_j - \sum_{i=1}^N y_ia_i^*(x_i \cdot x_j)
\end{aligned}(4)求得超平面 $w^* \cdot x + b = 0 $, 对于新的观测数据 $x$ , 根据 $f(x) = sign(w^* \cdot x+b^*)$ 判断其类别即可
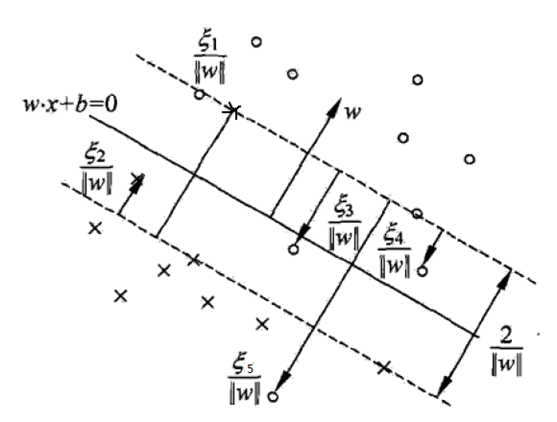
下图中实线为分离超平面,虚线为间隔边界,且有间隔边界与分离超平面的函数距离为1,几何距离为 $1/||w||$。在线性不可分的情况下,求借得到 $a^* = (a^*_1,a^*_2,…,a^*_N)$ 的分量 $a_i^*$ 对应的样本实例 $(x_i,y_i)$ 中的 $x_i$ 称为支持向量,这时的支持向量要比线性可分复杂一些,如下图的点,以下支持向量点到间隔边界的几何距离均已标注出为 $\xi_i/||w||$。这个几何距离是这样计算的,点 $x_i$ 到分离超平面的函数距离为 $y_i(w\cdot x_i+b) = 1- \xi_i$, 而分离超平面与间隔边界的函数距离为 1 ,所以点 $x_i$ 到间隔边界的距离为 $1-(1- \xi_i)$ ,几何距离只需除以 $||w||$ 即可得到结果。
可见这时候的支持向量或者分布在间隔边界上,或者在间隔边界与超平面之间,或者在分离超平面误分的一侧。 根据 KKT 条件可以得出一些很有意思的结论,当 $\gamma_i > 0 $ 时,根据 KKT 条件 (3) 可得 $C - a_i = \gamma_i >0$,即$ a_i <C$,又由于 $\gamma_i \xi_i = 0$可得 $\xi = 0$ ,根据 KKT 条件 (4) 可得 $a_i(y_i(w \cdot x +b) -1) = 0$ ,所以当 $0<a_i<C$ 时,可得$y_i(w \cdot x +b) =1$,这时样本便为支持向量,且落在间隔边界上;当 $a_i =0$ 时可得 $\xi_i = 0$ ,这时便为分类正确的且落在间隔边界之后的点,至于$a_i = C$ 的情况,根据 $\xi_i$ 的不同取值,可分为不同的情况,总结起来便有:
当 $0 < a_i^* < C$ :
$\xi_i = 0$ 这是 $x_i$ 为支持向量,且恰好落在间隔边界上
若 $a_i^* = C$
当 $0 < \xi_i < 1$ 时, 则分类正确 ,$x_i$ 落在间隔边界与分离超平面之间
当 $\xi_i = 1$ 时,则 $x_i$ 在分离超平面上
当 $\xi_i > 1$ 时 , 则 $x_i$ 位于分离超平面误分的一侧
至此,带有异常值的非线性可分的情况也解决了,但是还需要注意的是数据集是完全非线性可分的。这时便需要引入核方法了。核方法并不是 SVM 的专利,其可以解决一系列机器学习问题。
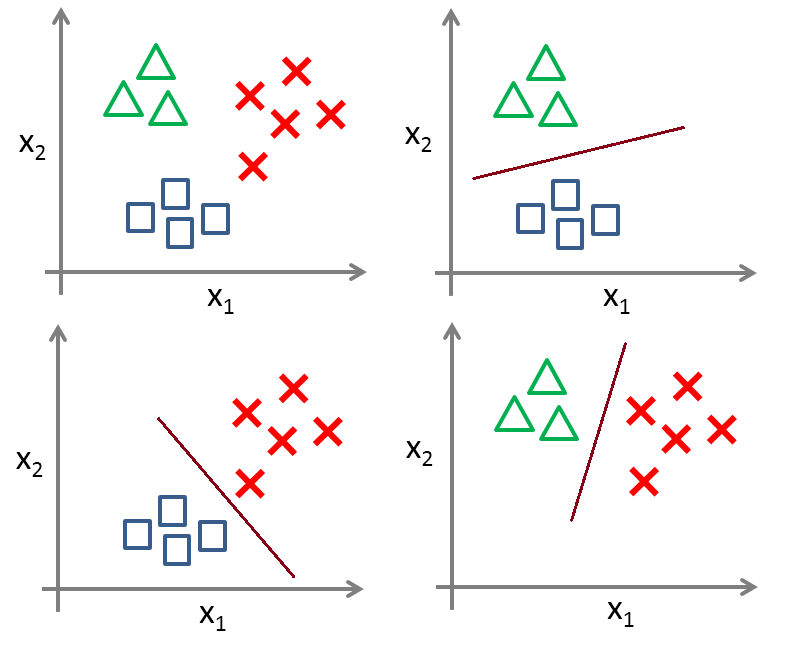
至于 K 分类问题 (K>2) ,最简单的方式便是 one-vs-all 的方法,如下图所示,该方法共训练 K 个分类器,对于待分类样本点,分别使用这 K 个分类器进行分类,对于样本 $x$ 分类的计算如下: $f(x)=sign(w \cdot x + b)$,若只有一个 +1 出现,则其为样本对应类别 k ;但实际情况下构造的决策函数总是有误差的,此时输出不只一个 +1 (不只一类声称它属于自己),或者没有一个输出为 +1 (即没有一个类声称它属于自己),这时比较则比较 $w \cdot x + b$ 输出值,最大者对应类别为样本 x 的类别 k 。
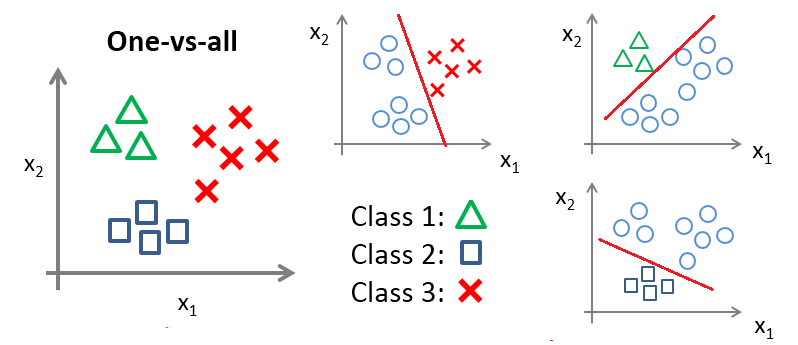
或者采用 LIBSVM 中 one-vs-one 的方法,其做法是在任意两类样本之间设计一个SVM,因此 k 个类别的样本就需要设计 $k(k-1)/2$ 个SVM。当对一个未知样本 进行分类时,最后得票最多的类别即为该未知样本的类别。比如说 A,B,C 四类。在训练的时候针对 (A,B) (A,C) (B,C) 所对应的样本作为训练集,然后得到六个模型,在测试的时候,对应的分别对三个模型进行测试,然后采取投票形式得到最后的结果,如下图所示:
再就是直接使用 Hinge Loss 进行多分类了,参考文章开头给出的连接即可。
参考:
统计学习方法
拉格朗日对偶 这两篇为个人博客中关于SVM的基础
http://www.cnblogs.com/v-July-v/archive/2012/06/01/2539022.html july
http://blog.pluskid.org/?page_id=683 pluskid
http://www.cnblogs.com/jerrylead/archive/2011/03/13/1982639.html jerrylead