(五)用正则化(Regularization)来解决过拟合
1 过拟合
过拟合就是训练模型的过程中,模型过度拟合训练数据,而不能很好的泛化到测试数据集上。出现over-fitting的原因是多方面的:
1) 训练数据过少,数据量与数据噪声是成反比的,少量数据导致噪声很大
2 )特征数目过多导致模型过于复杂,如下面的图所示:
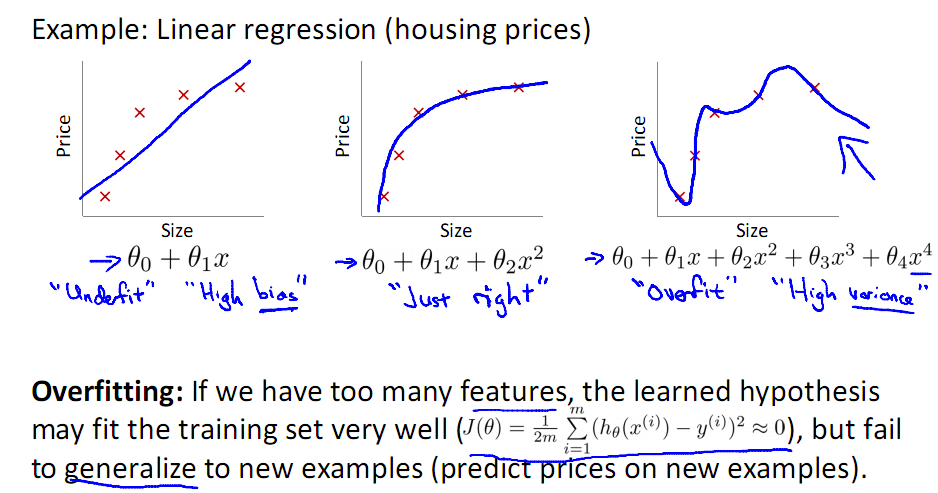
看上图中的多项式回归(Polynomial regression),左边为模型复杂度很低,右边的模型复杂度就过高,而中间的模型为比较合适的模型,对于Logistic有同样的情况

2)如何避免过拟合
1) 控制特征的数目,可以通过特征组合,或者模型选择算法
2)Regularization,保持所有特征,但是减小每个特征的参数向量θ的大小,使其对分类y所做的共享很小

下面来详细分析正则化
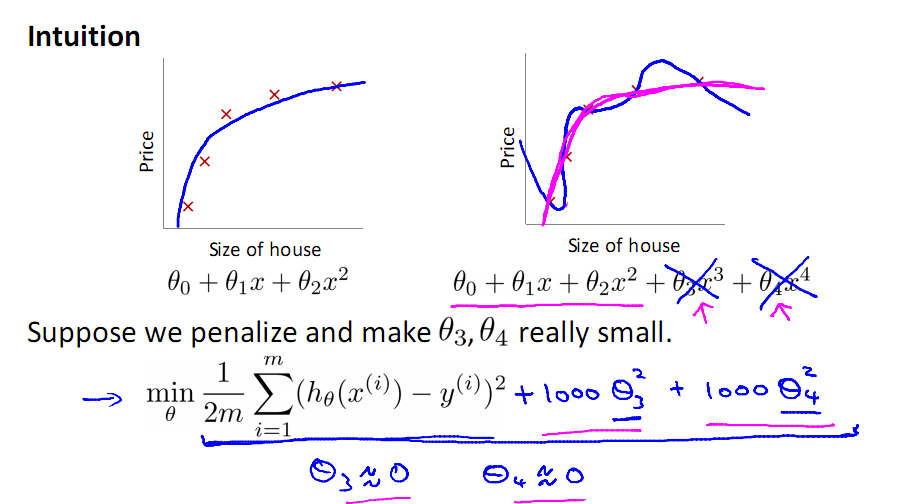
来看多项式拟合的问题,对于右图复杂的模型,只需控制θ3与θ4的大小,即可使得模型达到与作图类似的结果,下面引入线性回归的L2正则的公式

如上过程就是正则化的过程,注意正则化是不带θ0的,其实带不带在实际运用中只会有很小的差异,所以不必在意,现在只需要控制λ的大小,当λ很大时,θ1到θn就会很小,即达到了约束数量庞大的特征的目的。
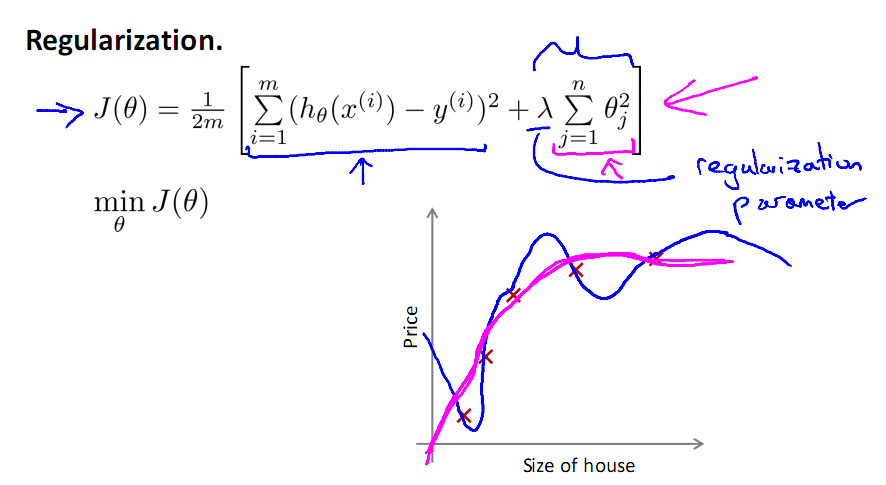
若选择过大的λ,会使得参数向量θ非常小,从而只剩下θ0,使得模型看起来像一条直线

而且,模型会欠拟合,梯度下降也不会收敛,而λ的选择将在特征选择中讲到

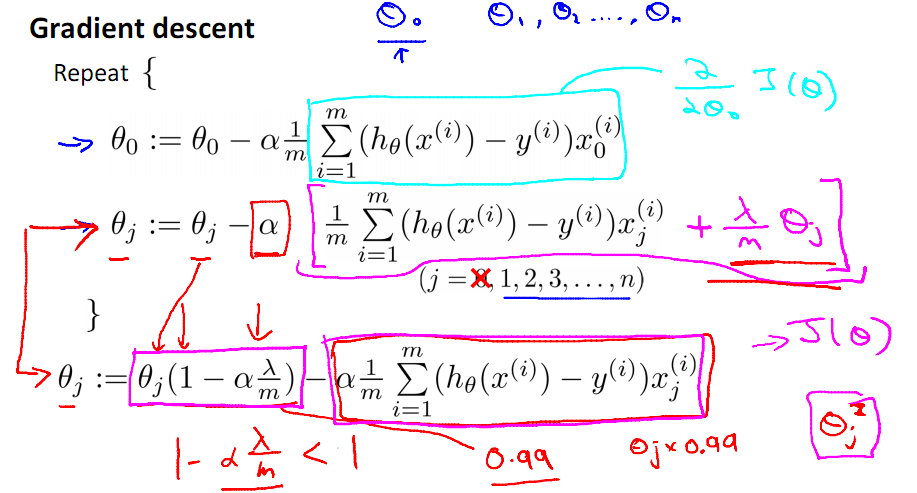
带有正则化项的梯度下降算法,首先要特殊处理θ0,
关于Normal Equation 的正则化

并且有一个不错的消息就是括号中的矩阵必定为可逆的
Logistic的正则化
首先看L2正则
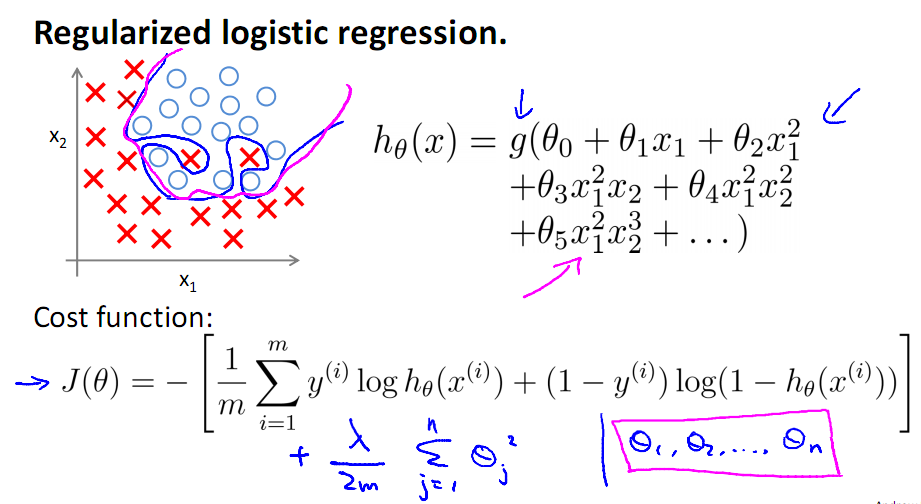
其正则化的Gradient Descent形式:

3 正则化的一些概念
1)概念
L0正则化的值是模型参数中非零参数的个数。
L1正则化表示各个参数绝对值之和。
L2正则化标识各个参数的平方的和的开方值。
2)正则化后会导致参数稀疏,一个好处是可以简化模型,避免过拟合。因为一个模型中真正重要的参数可能并不多,如果考虑所有的参数起作用,那么可以对训练数据可以预测的很好,但是对测试数据就只能呵呵了。另一个好处是参数变少可以使整个模型获得更好的可解释性。
且参数越小,模型就会越简单,这是因为越复杂的模型,越是会尝试对所有的样本进行拟合,甚至包括一些异常样本点,这就容易造成在较小的区间里预测值产生较大的波动,这种较大的波动也反映了在这个区间里的导数很大,而只有较大的参数值才能产生较大的导数。因此复杂的模型,其参数值会比较大。
3)三种正则概述
-》L0正则化
根据上面的讨论,稀疏的参数可以防止过拟合,因此用L0范数(非零参数的个数)来做正则化项是可以防止过拟合的。
从直观上看,利用非零参数的个数,可以很好的来选择特征,实现特征稀疏的效果,具体操作时选择参数非零的特征即可。但因为L0正则化很难求解,是个NP难问题,因此一般采用L1正则化。L1正则化是L0正则化的最优凸近似,比L0容易求解,并且也可以实现稀疏的效果。
-》L1正则化
L1正则化在实际中往往替代L0正则化,来防止过拟合。在江湖中也人称Lasso。
L1正则化之所以可以防止过拟合,是因为L1范数就是各个参数的绝对值相加得到的,我们前面讨论了,参数值大小和模型复杂度是成正比的。因此复杂的模型,其L1范数就大,最终导致损失函数就大,说明这个模型就不够好。
-》L2正则化
L2正则化可以防止过拟合的原因和L1正则化一样,只是形式不太一样。
L2范数是各参数的平方和再求平方根,我们让L2范数的正则项最小,可以使W的每个元素都很小,都接近于0。但与L1范数不一样的是,它不会是每个元素为0,而只是接近于0。越小的参数说明模型越简单,越简单的模型越不容易产生过拟合现象。
L2正则化江湖人称Ridge,也称“岭回归”
4)几何解释
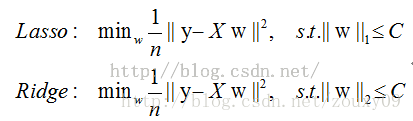
我们考虑两维的情况,在(w1, w2)平面上可以画出目标函数的等高线,而约束条件则成为平面上半径为C的一个 norm ball 。等高线与 norm ball 首次相交的地方就是最优解:
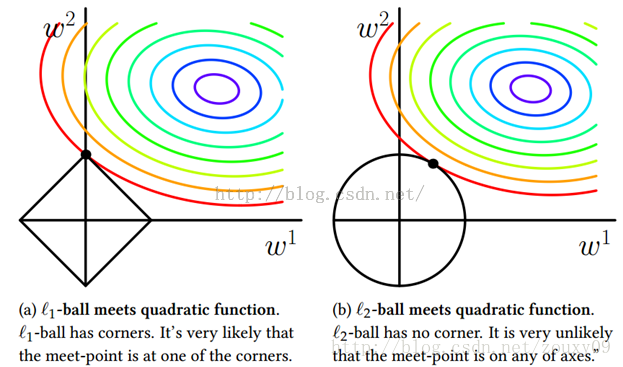
可以看到,L1-ball 与L2-ball 的不同就在于L1在和每个坐标轴相交的地方都有“角”出现,有很大的几率等高线会和L1-ball在四个角,也就是坐标轴上相遇,坐标轴上就可以产生稀疏,因为某一维可以表示为0。而等高线与L2-ball在坐标轴上相遇的概率就比较小了。
总结:L1会趋向于产生少量的特征,而其他的特征都是0,而L2会选择更多的特征,这些特征都会接近于0。Lasso在特征选择时候非常有用,而Ridge就只是一种规则化而已。在所有特征中只有少数特征起重要作用的情况下,选择Lasso比较合适,因为它能自动选择特征。而如果所有特征中,大部分特征都能起作用,而且起的作用很平均,那么使用Ridge也许更合适。
参考:1) NG讲义


