(原創) 如何處理signed integer的加法運算與overflow? (SOC) (Verilog)

Abstract
若要將原本用軟體實現的演算法用硬體電路實現，馬上會遇到2個很基本的問題：一個是如何處理負數?另一個是如何處理overflow?雖然很基本，但一旦有問題卻很難debug。

Introduction
使用環境：NC-Verilog 5.4 + Debussy 5.4 v9

一般在開發演算法階段，我們會使用C/C++這些高階語言開發，C/C++處理負數乘加運算都很方便與直覺，也不用太擔心overflow的問題，主要是int是4 byte(32 bit)夠大，要overflow也不太容易，若一旦要用硬體電路實現，馬上就面臨2個基本的問題，硬體要怎麼處理負數?要怎麼處理overflow?

Verilog在宣告reg與wire時，雖然能使用+ – * /，並合成出相對的加法器、乘法器與除法器，但這些都是無號數(unsigned integer)運算，也就是說只能做大於或等於0的整數加減乘除運算，無法處理負數運算；除此之外，不像C/C++的int就是32 bit，為了節省硬體cost，我們會根據值域，小心的宣告reg與wire的bit數，如只有4 bit或8 bit而已，這樣經過運算後，可能在某個boundary test pattern下，一不小心就overflow了。

在(原創) 無號數及有號數的乘加運算電路設計 (IC Design) (Verilog) (OS) (Linux)與(原創) 如何設計乘加電路? (SOC) (Verilog) (MegaCore)中，我都曾經討論過這個問題，這次打算更仔細重新討論，並將overflow議題一並考慮。

本文先討論加法運算部分，乘法部分將另開專文討論之‧

Verilog的運算
Verilog所提供的運算分unsigned與signed兩種：

  • Unsigned：不含signed bit
    • 以4 bit來說，值域從0000~1111，也就是0 ~ 15
  • Signed：含signed bit(MSB為signed bit，1為負，0為正，負數使用2補數表示)
    • 以4 bit來說，值域從1000~0111，也就是-8 ~ +7

二進位signed加法運算
在真正開始使用Verilog做signed加法運算前，我們先來看看實際上二進位singed加法是如何運算?

Normal Condition (沒有Overflow)
(+6) + (-3) = (+3)

為了節省resource，我們故意使用4 bit的+6與3 bit的-3相加，若直接將兩個signed值相加，答案為-7，很顯然答案並不正確‧

add00

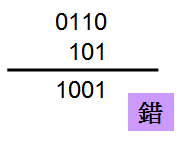
因為4 bit與3 bit相加，結果可能進位到5 bit，正確的作法是將4 bit的+6做signed extension到5 bit，且3 bit的-3也要做signed extension到5 bit後，然後才相加，若最後進位到6 bit，則不考慮6 bit的值‧

add01 

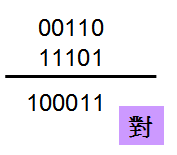
在此補充一下何謂Singed Extension?簡單的說，當以較多bit顯示signed型態的值時，重複signed bit補齊‧

add02

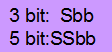
就意義上來說，就是3 bit的signed值若要以5 bit表示時，必須補上signed bit才能在5 bit表示，所以101要變成11101‧

Boundary Condition (正Overflow)
(+7) + (+3) = (+10)

為了節省resource，我們一樣故意使用4 bit的+7與3 bit的+3相加，若直接將兩個signed值相加，答案為-6，很顯然答案並不正確。

add03

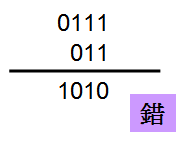
根據上個例子的經驗，+7與+3必須做signed extension才能相加，這樣才能得到正確答案+10‧

add04

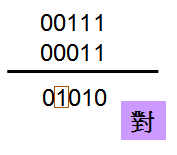
不過現在問題來了，+10必須動到5 bit才能顯示，若輸出的值域為4 bit，只能-8 ~ +7，+10很顯然已經正overflow了‧

若只能以4 bit表示，因為是正的，MSB必須是0(SUM[3]=0)，所以若MSB是1就表示由進位而來，也就是正overflow了(此例的SUM[3]為1，所以已經正overflow)，再加上因為目前運算結果為5 bit，且是正，所以SUM[5]必須為0。

也就是說，若SUM[5]=0且SUM[4]=1時，為正overflow，所以01010對於4 bit來說，是正overflow。

Boundary Condition (負Overflow)
(-5) + (-4) = (-9)

同樣為了節省resource，我們故意使用4 bit的-5與3 bit的-4相加，若直接將兩個signed值相加，答案為-1，很顯然的答案並不正確‧

add05

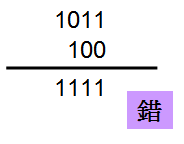
根據前面兩個例子，-5與-4一樣必須做signed extension才能相加，這樣才能得到正確答案-9‧進位到6 bit的1要捨去，所以答案是10111‧

add06

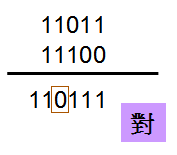
問題一樣來了，-9必須動到5 bit才能顯示，若輸出的值域是4 bit，只能-8 ~ +7，-9很顯然已經是負overflow了‧

若只能以4 bit表示，因為是負的，MSB必須是1(SUM[3]=1)，所以若MSB是0就表示由進位而來，也就是負overflow了(此例的SUM[3]為0，所以已經負overflow)，再加上因為目前運算結果為5 bit，且是負，所以SUM[5]必須為1‧

也就是說，若SUM[5]為1且SUM[4]為0時，為負overflow，所以10111對於4 bit來說，是負overflow‧

二進位Signed加法運算Summary

根據之前三個實際的例子，我們得到以下結論

  • m bit + m bit => (m+1) bit
  • m bit + n bit => (m+1) bit，其中n < m
    • m bit與n bit都必須先做signed extension到(m+1) bit才能相加
    • 若結果有到(m+2) bit則忽略之，實際的結果為(m+1) bit
  • 若Sum[m+1] ^ Sum[m]為1，表示有overflow
    • 若Sum[m+1]為0且Sum[m]為1，則為正overflow
    • 若Sum[m+1]為1且Sum[m]為0，則為負overflow

 

使用Verilog實現
signed_add.v / Verilog

1 /* 
2 (C) OOMusou 2009 http://oomusou.cnblogs.com
3 
4 Filename    : signed_add.v
5 Simulator   : NC-Verilog 5.4 + Debussy 5.4 v9
6 Description : signed add & overflow
7 Release     : Oct/24/2009 1.0
8 */
9 
10 module signed_add (
11   clk,
12   rst_n,
13   a_i,
14   b_i,
15   sum_o
16 );
17 
18 input clk;
19 input rst_n;
20 input [3:0] a_i;
21 input [2:0] b_i;
22 output [3:0] sum_o;
23 
24 reg [4:0] sum_t;
25 always@(posedge clk or negedge rst_n)
26   if (~rst_n)
27     sum_t <= 5'h0;
28   else
29     sum_t <= {a_i[3], a_i} + {{2{b_i[2]}}, b_i};
30    
31 assign sum_o = (~sum_t[4] &  sum_t[3]) ? 4'b0111 : // + overflow
32                ( sum_t[4] & ~sum_t[3]) ? 4'b1000 : // - overflow
33                sum_t[3:0];
34 endmodule


20 ~ 22行

input [3:0] a_i;
input [2:0] b_i;
output [3:0] sum_o;


輸入一個為3 bit，一個為4 bit，輸出為4 bit，與之前舉的例子一樣‧

29行

sum_t <= {a_i[3], a_i} + {{2{b_i[2]}}, b_i};


將4 bit的a_i做signed extension到5 bit，將3 bit的b_i做signed extension到5 bit‧

31行

(~sum_t[4] &  sum_t[3]) ? 4'b0111 : // + overflow


判斷是否為正overflow，若sum_t[4]為0且sum_t[3]為1，則為正overflow‧

32行

( sum_t[4] & ~sum_t[3]) ? 4'b1000 : // - overflow


判斷是否為負overflow，若sum_t[4]為1且sum_t[3]為0，則為負overflow‧

Testbench
signed_add_tb.v / Verilog 

1 /* 
2 (C) OOMusou 2009 http://oomusou.cnblogs.com
3 
4 Filename    : signed_add_tb.v
5 Simulator   : NC-Verilog 5.4 + Debussy 5.4 v9
6 Description : signed add & overflow testbench
7 Release     : Oct/24/2009 1.0
8 */
9 
10 `include "signed_add.v"
11 
12 module signed_add_tb;
13 
14 reg clk;
15 reg rst_n;
16 reg [3:0] a_i;
17 reg [2:0] b_i;
18 wire [3:0] sum_o;
19 
20 // 4 bit
21 // -8 ~ +7
22 // 3 bit
23 // -4 ~ +3
24 initial begin
25   //a_i <= 4'b0000;
26   //b_i <= 3'b000;
27   a_i <= 4'd0;
28   b_i <= 3'd0;
29  
30   // normal
31   // (+6) + (-3)
32   #10;
33   //a_i <= 4'b0110;
34   //b_i <= 3'b101;
35   a_i <= 4'd6;
36   b_i <= -3'd3;
37  
38   // overflow
39   // 7 + 3 = 10
40   #20;
41   //a_i <= 4'b0111;
42   //b_i <= 3'b011;
43   a_i <= 4'd7;
44   b_i <= 3'd3;
45  
46   // underflow
47   // (-5) + (-4)
48   #20;
49   //a_i <= 4'b1011;
50   //b_i <= 3'b100;
51   a_i <= -4'd5;
52   b_i <= -3'd4;
53  
54   #20;
55   //a_i <= 4'b0000;
56   //b_i <= 3'b000;
57   a_i <= 4'd0;
58   b_i <= 3'd0;
59 end
60 
61 
62 initial clk = 1'b0;
63 always #10 clk = ~clk;
64 
65 initial begin
66   rst_n = 1'b0;
67   #5;
68   rst_n = 1'b1;
69 end
70 
71 initial begin
72   $fsdbDumpfile("signed_add.fsdb");
73   $fsdbDumpvars(0, signed_add_tb);
74   #100;
75   $finish;
76 end
77 
78 signed_add signed_add0 (
79   .clk(clk),
80   .rst_n(rst_n),
81   .a_i(a_i),
82   .b_i(b_i),
83   .sum_o(sum_o)
84 );
85 
86 
87 endmodule


模擬結果

add08 

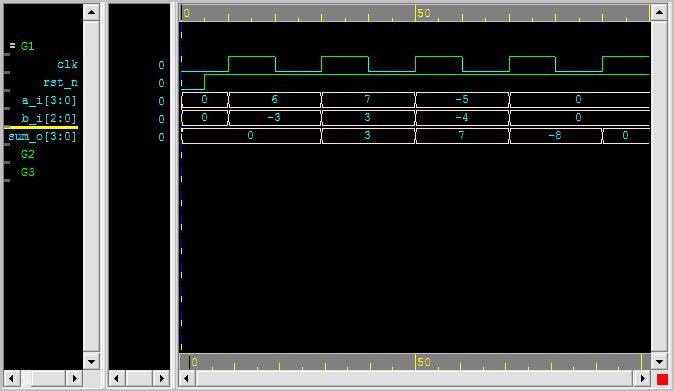
7 + 3 = 10，因為已經正overflow，所以使用4 bit最大值+7表示‧
(-5) + (-4) = (-9)，因為已經負overflow，所以使用4 bit最小值-8表示‧

 

完整程式碼下載
signed_add.7z

Conclusion
本文詳細討論了在數位電路與Verilog中，如何執行帶負數的加法，以及如何判斷overflow等課題，雖然非常基本，但在使用硬體實現演算法時卻非常重要，下一次將討論如何在數位電路與Verilog實現帶負數的乘法‧

See Also
(原創) 如何設計乘加電路? (SOC) (Verilog) (MegaCore)
(原創) 無號數及有號數的乘加運算電路設計 (IC Design) (Verilog) (OS) (Linux)
(原創) 如何用管線(Pipeline)實作無號數乘加運算? (IC Design) (Verilog)
(原創) 如何設計2數相加的電路? (SOC) (Verilog)

posted on 2009-10-31 10:48  真 OO无双  阅读(84406)  评论(6)  编辑  收藏  举报

导航