【BZOJ】3529: [Sdoi2014]数表

【题意】令F(i)为 i 的约数和，Q次询问给定n,m,a，求：ΣF(gcd(i,j))%2^31，1<=i<=n，1<=j<=m，F(gcd(i,j))<=a。n,m<=10^5，a<=10^9，Q<=20000。

【算法】数论（莫比乌斯反演）

【题解】先无视a的限制，令g(x)表示gcd(a,b)=x的数对个数，则由莫比乌斯反演定理易得

g(x) = Σ_x|d μ(d/x) * (n/d) * (m/d)

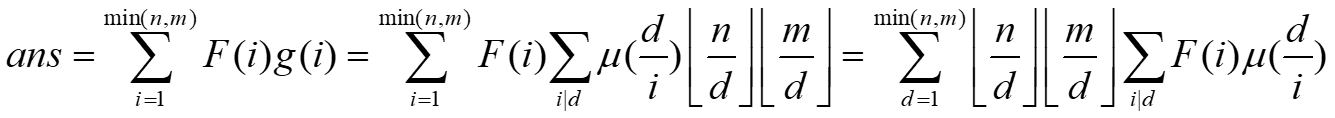
图片来源：PoPoQQQ课件

那么只要有最后Σ_i|dF(i)*μ(d/i)的前缀和，就可以用取值分块优化的方法快速求解。

F(i)可以用线性筛O(n)预处理（i%prime[j]==0时f[i*prime[j]]=f[i]+f[i/e[i]]*e[i]*prime[j]，e[i]=p^a，p为i的最小素因子，a为其幂次），当然枚举倍数求更方便。

然后只需要参考YY的GCD枚举倍数贡献就可以了。

最后是F(gcd(i,j))<=a，只有F(i)<=a时有贡献。将询问离线，F(i)从小到大排序后依次计算，用树状数组维护前缀和。

复杂度O(n*(ln n)*(log n)+Q*√n*log n)

取模2^31相当于int自然溢出最后和2^31-1取与，原因大概和负数的二进制表示有关，不深究。

#include<cstdio>
#include<algorithm>
#define lowbit(x) (x&-x)
using namespace std;
const int maxn=100010,N=100000;

struct cyc{int n,m,a,id;}nn[maxn];
struct node{int num,id;}f[maxn];
int miu[maxn],prime[maxn],tot,e[maxn],c[maxn],ANS[maxn];
bool mark[maxn];
bool cmp2(node a,node b){return a.num<b.num;}
void pre(int n){
    miu[1]=f[1].num=e[1]=1;
    for(int i=2;i<=n;i++){
        if(!mark[i]){
            miu[prime[++tot]=i]=-1;
            f[i].num=i+1;
            e[i]=i;
        }
        for(int j=1;j<=tot&&i*prime[j]<=n;j++){
            mark[i*prime[j]]=1;
            if(i%prime[j]==0){
                miu[i*prime[j]]=0;
                f[i*prime[j]].num=f[i].num+f[i/e[i]].num*e[i]*prime[j];
                e[i*prime[j]]=e[i]*prime[j];
                break;
            }
            miu[i*prime[j]]=-miu[i];
            f[i*prime[j]].num=f[i].num*(prime[j]+1);
            e[i*prime[j]]=prime[j];
        }
    }
    for(int i=1;i<=N;i++)f[i].id=i;
    sort(f+1,f+N+1,cmp2);
}
bool cmp(cyc a,cyc b){return a.a<b.a;}
void modify(int x,int k){for(int i=x;i<=N;i+=lowbit(i))c[i]+=k;}
int ask(int x){int as=0;for(int i=x;i>=1;i-=lowbit(i))as+=c[i];return as;}
int main(){
    pre(N);
    int T;
    scanf("%d",&T);
    for(int i=1;i<=T;i++)scanf("%d%d%d",&nn[i].n,&nn[i].m,&nn[i].a),nn[i].id=i;
    sort(nn+1,nn+T+1,cmp);
    int pre=0;
    for(int TT=1;TT<=T;TT++){
        int n=nn[TT].n,m=nn[TT].m,a=nn[TT].a;
        while(pre+1<=N&&f[pre+1].num<=a){
            pre++;
            for(int j=f[pre].id;j<=N;j+=f[pre].id)modify(j,f[pre].num*miu[j/f[pre].id]);
        }
        int pos=0,mins=min(n,m),ans=0;
        for(int i=1;i<=mins;i=pos+1){
            pos=min(n/(n/i),m/(m/i));
            ans+=(ask(pos)-ask(i-1))*(n/i)*(m/i);
        }
        ANS[nn[TT].id]=ans&0x7fffffff;
    }
    for(int i=1;i<=T;i++)printf("%d\n",ANS[i]);
    return 0;
}

 

另一种思路，尝试用基本反演形式e=i*μ来推导。

$$ans=\sum_ {g\leq min(n,m)}F(g)\sum_{i\leq n}\sum_{j\leq m}[gcd(i,j)=g]$$

$$ans=\sum_ {g\leq min(n,m)}F(g)\sum_{d\leq min(n/g,m/g))}\mu (d)\left \lfloor n/gd \right \rfloor\left \lfloor m/gd \right \rfloor$$

（这步见Problem b）

令T=gd

$$ans=\sum_{T\leq min(n,m)}\left \lfloor n/T \right \rfloor\left \lfloor m/T \right \rfloor \sum_{g|T}F(g)\mu (T/g)$$

（这步类似YY的GCD）

然后后面预处理前缀和，前面√n回答询问。