从2-3-4树到红黑树(下) Java与C的实现

欢迎探讨，如有错误敬请指正

如需转载，请注明出处   http://www.cnblogs.com/nullzx/

相关博客：

从2-3-4树到红黑树（上）

从2-3-4树到红黑树（中）

 

1. 实现技巧

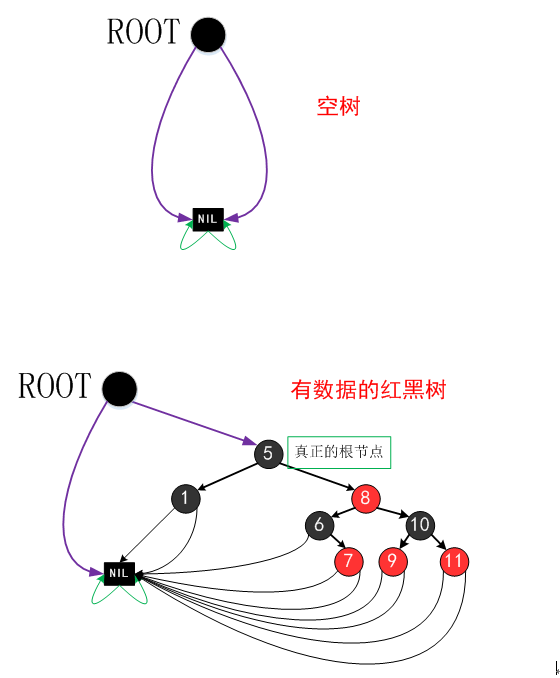
为了简化代码和减少不必要的开销，在具体的实现中我们定义一个伪根节点ROOT且只定义一个NIL节点。伪根节点的左子支永远指向NIL节点，NIL节点的左右子支又指向它自身。伪根节点的右子支才表示真正的红黑树。

2. Java语言实现

package datastruct;

import java.util.Comparator;


public class RBtree<E> {
	private static class Node<E>{
		E e;
		boolean color;
		Node<E> left;
		Node<E> right;
		Node<E> parent;
		
		public Node(E e, boolean color, Node<E> left, Node<E> right, Node<E> parent){
			this.e = e;
			this.color = color;
			this.left = left;
			this.right = right;
			this.parent = parent;
		}
		
		public boolean isRead(){
			return color;
		}
	}
	
	public static final boolean RED = true;
	public static final boolean BLACK = false;
	
	//所有叶子节点的左右子支都指向同一个NIL节点,NIL节点的父节点指向null
	private final Node<E> NIL; 
	private final Node<E> ROOT;//指向伪根节点的引用
	private int size = 0;//节点个数
	Comparator<? super E> cmp;//节点大小的比较器
	
	//如果调用了不带参数的构造函数，则使用该内部类作为比较器，
	//但此时泛型E需要继承Comparable接口,否则运行时会抛出异常
	private static class Cmp<T> implements Comparator<T>{
		@SuppressWarnings({ "unchecked", "rawtypes" })
		@Override
		public int compare(T e1, T e2) {
			return ((Comparable)e1).compareTo(e2);
		}
		
	}
	
	//不带比较器的构造函数
	public RBtree(){
		ROOT = new Node<E>(null, BLACK, null, null, null);
		NIL = new Node<E>(null, BLACK, null, null, null);
		NIL.left = NIL;
		NIL.right = NIL;
		ROOT.left = NIL;
		ROOT.right = NIL;
		ROOT.parent = ROOT;
		cmp = new Cmp<E>();
	}
	
	//带比较器的构造函数
	public RBtree(Cmp<? super E> cmp){
		if(cmp == null){
			throw new IllegalArgumentException();
		}
		this.cmp = cmp;
		//创建一个伪根节点，该节点的右子支才是真正的RBtree树的根,同时该节点还作为NIL节点
		//使用伪根节点节点的目的是，对插入和删除操作递归的形式能够统一
		ROOT = new Node<E>(null, BLACK, null, null, null);
		NIL = new Node<E>(null, BLACK, null, null, null);
		NIL.left = NIL;
		NIL.right = NIL;
		ROOT.left = NIL;
		ROOT.right = NIL;
		ROOT.parent = ROOT;
	}
	
	//逆时针旋转（左旋），参数表示轴节点
	private void antiClockwiseRotate(Node<E> X){
		Node<E> P = X.parent;
		Node<E> XR = X.right;
		if(P.left == X){
			P.left = XR;
		}else{
			P.right = XR;
		}
		XR.parent = P;
		
		X.right = XR.left;
		if(XR.left != NIL){
			XR.left.parent = X;
		}
		
		XR.left = X;
		X.parent = XR;
	}
	
	//顺时针旋转（右旋）,参数表示轴节点
	private void clockwiseRotate(Node<E> X){
		Node<E> P = X.parent;
		Node<E> XL = X.left;
		if(P.left == X){
			P.left = XL;
		}else{
			P.right = XL;
		}
		XL.parent = P;
		
		X.left = XL.right;
		if(XL.right != NIL){
			XL.right.parent = X;
		}
		
		XL.right = X;
		X.parent = XL;
	}
	
	private Node<E> min(Node<E> X){		
		while(X.left != NIL){
			X = X.left;
		}
		return X;
	}
	
	public int size(){
		return size;
	}
	
	public boolean contain(E e){
		Node<E> X = ROOT.right;
		while(X != NIL){
			int r = cmp.compare(e, X.e);
			if(r > 0){
				X = X.right;
			}else
			if(r < 0){
				X = X.left;
			}else{
				return true;
			}
		}
		return false;
	}
	
	public boolean insert(E e){
		Node<E> P = ROOT;
		Node<E> X = ROOT.right;
		int r = 0;
		while(X != NIL){
			r = cmp.compare(e, X.e);
			P = X;
			if(r > 0){
				X = X.right;
			}else
			if(r < 0){
				X = X.left;
			}else{
				return false;//元素已存在，插入失败
			}
		}
		
		Node<E> G;
		Node<E> U;
		X = new Node<E>(e, RED, NIL, NIL, P);//插入的新节点涂红
		if(r >= 0){//考虑到首次插入的情况，这个等号是必须的
			P.right = X;
		}else{
			P.left = X;
		}
		
		while(true){
			P = X.parent;
			
			//红父
			if(P.isRead()){
				G = P.parent;
				
				if(P == G.left){
					U = G.right;
				}else{
					U = G.left;
				}
				
				//红叔
				if(U.isRead()){
					P.color = BLACK;
					U.color = BLACK;
					G.color = RED;
					X = G;//继续向上回溯
				}else{//黑叔
					if(G.left == P){
						if(P.left == X){
							clockwiseRotate(G);
							P.color = BLACK;
							G.color = RED;
						}else{
							antiClockwiseRotate(P);
							clockwiseRotate(G);
							X.color = BLACK;
							G.color = RED;
						}
					}else{
						if(P.right == X){
							antiClockwiseRotate(G);
							P.color = BLACK;
							G.color = RED;
						}else{
							clockwiseRotate(P);
							antiClockwiseRotate(G);
							X.color = BLACK;
							G.color = RED;
						}
					}
					break;
				}
			}else{//黑父
				break;
			}
		}
		size++;
		ROOT.right.color = BLACK;//有可能向上层进位，根节点图黑
		return true;
	}
	
	public boolean delete(E e){
		Node<E> X = ROOT.right;
		X.color = RED; //删除时，根先涂红，1.防止继续向上回溯  2.只有根节点时也方便删除
		Node<E> P;
		Node<E> B;
			
		while(X != NIL){
			int r = cmp.compare(e, X.e);
			if(r > 0){
				X = X.right;
			}else
			if(r < 0){
				X = X.left;
			}else{
				break;
			}
		}
		
		if(X == NIL){//没有找到需要删除的节点
			ROOT.right.color = BLACK;
			return false;
		}
		
		size--;//一定可以删除一个节点
		if(X.left != NIL && X.right != NIL){
			Node<E> tmp = min(X.right);
			X.e = tmp.e;
			X = tmp;	
		}
		
		P = X.parent;
		if(X.right != NIL){
			if(X == P.left){
				P.left = X.right;
			}else{
				P.right = X.right;
			}
			X.right.parent = P;
			X.color = BLACK;
			ROOT.right.color = BLACK;
			return true;
		}else
		if(X.left != NIL){
			if(X == P.left){
				P.left = X.left;
			}else{
				P.right = X.left;
			}
			X.left.parent = P;
			X.color = BLACK;
			ROOT.right.color = BLACK; 
			return true;
		}else{
			if(X == P.left){
				P.left = NIL;
			}else{
				P.right = NIL;
			}
			
			if(X.isRead()){
				ROOT.right.color = BLACK;
				return true;
			}else{
				X = NIL;
			}
		}
		
		//要删除的是叶子节点
		//四中情况调整
		while(true){
			if(X == P.left){
				B = P.right;
			}else{
				B = P.left;
			}
			
			if(!B.isRead()){//黑兄
				Node<E> BL = B.left;//左侄子
				Node<E> BR = B.right;//右侄子
				if(B.left.isRead() || B.right.isRead()){//红侄
					if(X == P.left){
						if(BR.isRead()){
							antiClockwiseRotate(P);
							BR.color = BLACK;
							B.color = P.color;
							P.color = BLACK;
						}else{
							clockwiseRotate(B);
							antiClockwiseRotate(P);
							BL.color = P.color;
							P.color = BLACK;
						}
					}else{
						if(BL.isRead()){
							clockwiseRotate(P);
							BL.color = BLACK;
							B.color = P.color;
							P.color = BLACK;
						}else{
							antiClockwiseRotate(B);
							clockwiseRotate(P);
							BR.color = P.color;
							P.color = BLACK;
						}
					}
					break;//不需要继续向上回溯
				}else{
					if(P.isRead()){//黑侄红父
						P.color = BLACK;
						B.color = RED;
						break;//不需要继续向上回溯
					}else{//黑侄黑父,继续向上回溯
						B.color = RED;
						X = P;
						P = X.parent;
					}
				}
			}else{//红兄，变换一下红黑树的形状，继续判断
				if(B == P.right){
					antiClockwiseRotate(P);
				}else{
					clockwiseRotate(P);
				}
				B.color = BLACK;
				P.color = RED;
				//X节点的P节点没有发生变化，但兄弟节点发生变化
			}
		}
		ROOT.right.color = BLACK;
		return true;
	}
	
	public void preorderTraverse(){
		preorderTraverse0(ROOT.right);
	}
	
	private void preorderTraverse0(Node<E> X){
		if(X != NIL){
			System.out.print(X.e + "    " + (X.isRead() ? "RED  " : "BLACK") + "   :");
			if(X.left != NIL){
				System.out.print(X.left.e + "   ");
			}else{
				System.out.print("NIL  ");
			}
			
			if(X.right != NIL){
				System.out.print(X.right.e + "   ");
			}else{
				System.out.print("NIL  ");
			}
			System.out.println();
			preorderTraverse0(X.left);
			preorderTraverse0(X.right);
		}
	}
	
	public static void main(String[] args){
		RBtree<Integer> rbt = new RBtree<Integer>();
		rbt.insert(50);
		rbt.insert(25);
		rbt.insert(75);
		rbt.insert(10);
		rbt.insert(30);
		rbt.insert(27);
		rbt.insert(35);
		rbt.insert(40);
		rbt.insert(31);
		rbt.insert(55);
		rbt.insert(80);
		rbt.insert(90);
//		rbt.insert(22);
//		rbt.insert(5);
//		rbt.delete(5);
//		rbt.delete(51);
//		rbt.delete(80);
//		rbt.delete(50);
//		rbt.delete(75);
//		rbt.delete(27);
//		rbt.delete(10);
//		rbt.delete(25);
		rbt.delete(10);
		rbt.preorderTraverse();
		System.out.println();
		System.out.println("size: " + rbt.size());
		System.out.println(rbt.contain(40));
	}
}

 

3. C语言实现

下面的C语言实现是自顶向下的方式实现的，即采用了预合并和预分裂的方法，详情请见本博客 从2-3-4到红黑树（上）。在此方法中我们将伪根节点的数据定义为负无穷，这样插入和删除操作可以直接从伪根节点开始。

"RBtree.h"中的文件内容

#ifndef __RBTREE_H__
#define __RBTREE_H__

typedef enum{Red,Black} colorType;
typedef struct Node{
	int data;
	struct Node* left;
	struct Node* right;
	colorType color;
}Node,*RBtree;

int Insert(RBtree* T, int argD);
int Delete(RBtree* T, int argD);
int Find(RBtree T,int argD);
int InOredrTraverse(RBtree T);
int PreOredrTraverse(RBtree T);
int Destroy(RBtree* T);

#endif

 

RBtree.c中的内容

#include "RBtree.h"
#include <limits.h>
#include <stdlib.h>
#include <stdio.h>

static int Init(RBtree* T);
static int FindMin(Node* ptr,RBtree NullNode);
static void RightRotate(RBtree* T);
static void LeftRotate(RBtree* T);

static void RightPreOrderTra(RBtree ptr,RBtree NullNode);
static void RightInOrderTra(RBtree ptr,RBtree NullNode);
static void RightPostOrderTra(RBtree ptr,RBtree NullNode);

int Insert(RBtree* T, int argD){
	Node *X,*P,*GP,*GGP,*NullNode;
	Node **tmp;
	if(T == NULL){
		return -1;
	}

	if(*T == NULL){
		if(Init(T) == -1){
			return -1;
		}
	}

	GP = NULL; 
	GGP = NULL;
	P = NULL; 
	X = (*T);//从头结点开始，防止插入负无穷
	NullNode = (*T)->left;
	NullNode->data = argD;
	
	while(X->data != argD){
		if(X->left->color == Red && X->right->color == Red){
			X->color = Red;
			X->left->color = Black;
			X->right->color = Black;

			if(P->color == Red){
				if(argD > GGP->data){
					tmp = &(GGP->right);
				}else{
					tmp = &(GGP->left);
				}

				if(argD > GP->data){
					if(argD > P->data){
						LeftRotate(tmp);
						P->color = Black;
						GP->color = Red;
						GP = GGP; //为能够正确下落一层做保证
					}else{
						RightRotate(&(GP->right));
						LeftRotate(tmp);
						X->color = Black;
						GP->color = Red;
						P = X;//为能够正确下落一层做保证
						GP = P;//为能够正确下落一层做保证
					}	
				}else{
					if(argD < P->data){
						RightRotate(tmp);
						P->color = Black;
						GP->color = Red;
						GP = GGP;
					}else{
						LeftRotate(&(GP->left));
						RightRotate(tmp);
						X->color = Black;
						GP->color = Red;
						P = X;
						GP = P;
					}	
				}
			}
		}

		GGP = GP; GP = P; P = X;
		if(argD > X->data){
			X = X->right;
		}
		else{
			X = X->left;
		}

	}

	if(X != NullNode){
		(*T)->right->color = Black;
		return -1;
	}

	X = (Node*)malloc(sizeof(Node));
	if(X == NULL){
		(*T)->right->color = Black;
		return -1;
	}

	X->color = Red;
	X->data = argD;
	X->left = X->right = NullNode;
	if(argD > P->data){
		P->right = X;
	}
	else{
		P->left = X;
	}

	if(P->color == Red){
		if(argD > GGP->data){
			tmp = &(GGP->right);
		}else{
			tmp = &(GGP->left);
		}

		if(argD > GP->data){
			if(argD > P->data){
				LeftRotate(tmp);
				P->color = Black;
				GP->color = Red;
				GP = GGP;
			}else{
				RightRotate(&(GP->right));
				LeftRotate(tmp);
				X->color = Black;
				GP->color = Red;
				P = X;
				GP = P;
			}	
		}else{
			if(argD < P->data){
				RightRotate(tmp);
				P->color = Black;
				GP->color = Red;
				GP = GGP;
			}else{
				LeftRotate(&(GP->left));
				RightRotate(tmp);
				X->color = Black;
				GP->color = Red;
				P = X;
				GP = P;
			}	
		}
	}

	(*T)->right->color = Black;
	return 0;
}

int Delete(RBtree* T,int argD){
	Node *X,*B,*P,*GP,*NullNode;
	RBtree *tmp;
	if(T == NULL || *T == NULL){
		return -1;
	}

	P = *T;
	X = (*T)->right;//X从root开始，防止删除负无穷
	NullNode = (*T)->left;
	B = NullNode; 
	GP = NULL;
	(*T)->right->color = Red;//根涂红
	
	while(1){
		if(X == NullNode){
			(*T)->right->color = Black;
			return -1;//删除元素不存在
		}
		
		if(X->color == Black){
			if(X->left->color == Black && X->right->color == Black){
				if(B->color == Red){
					if(GP->right == P){
						tmp = &(GP->right);
					}else{
						tmp = &(GP->left);
					}

					B->color = Black;
					P->color = Red;
					if(P->right == X){
						RightRotate(tmp);
						B = P->left;
						GP = *tmp;
					}else{
						LeftRotate(tmp);
						B = P->right;
						GP = *tmp;
					}
				}

				if(B->color == Black){
					if(B->left->color == Black && B->right->color == Black){
						P->color = Black;
						X->color = Red;
						B->color = Red;
					}else{
						if(GP->right == P){
							tmp = &(GP->right);
						}else{
							tmp = &(GP->left);
						}

						if(P->right == X){
							if(B->left->color == Red){
								P->color = Black;
								X->color = Red;
								B->color = Red;
								B->left->color = Black;
								RightRotate(tmp);
							}else
							if(B->right->color == Red){
								P->color = Black;
								X->color = Red;
								LeftRotate(&(P->left));
								RightRotate(tmp);
							}
						}else{
							if(B->right->color == Red){
								P->color = Black;
								X->color = Red;
								B->color = Red;
								B->right->color = Black;
								LeftRotate(tmp);								
							}else
							if(B->left->color == Red){
								P->color = Black;
								X->color = Red;
								RightRotate(&(P->right));
								LeftRotate(tmp);							
							}						
						}
					}	
				}
			}
		}

		if(X->data == argD){
			if(X->left != NullNode && X->right != NullNode){
				argD = FindMin(X->right,(*T)->left);
				X->data = argD;
				GP = P;
				P = X;
				X = P->right;
				B = P->left;
			}else
			if(X->left == NullNode && X->right == NullNode){
				if(P->right == X){
					P->right = NullNode;
				}
				else{
					P->left = NullNode;
				}
				free(X);

				if((*T)->left == NullNode && (*T)->right == NullNode){
					free(NullNode);
					free(*T);
					*T = NULL;
					return 0;
				}
				(*T)->right->color = Black;
				return 0;
			}else
			if(X->left != NullNode){
				X->data = X->left->data;
				free(X->left);
				X->left = NullNode;
				(*T)->right->color = Black;
				return 0;
			}else
			if(X->right != NullNode){
				X->data = X->right->data;
				free(X->right);
				X->right = NullNode;
				(*T)->right->color = Black;
				return 0;
			}
		}else
		if(argD > X->data){
				GP = P;
				P = X;
				X = P->right;
				B = P->left;
		}else
		if(argD < X->data){
				GP = P;
				P = X;
				X = P->left;
				B = P->right;
		}
	}
}

int Find(RBtree T,int argD){
	if(T != NULL){
		Node* root = T->right;
		Node* NullNode = T->left; 
		while(root != NullNode){
			if(root->data == argD){
				return 0;
			}else
			if(argD > root->data){
				root = root->right;	
			}else{
				root = root->left;	
			}
		}	
	}
	return -1;

}

int InOredrTraverse(RBtree T){
	if(T == NULL){
		return -1;
	}
	RightInOrderTra(T->right, T->left);
	return 0;
}

int PreOredrTraverse(RBtree T){
	if(T == NULL){
		return -1;
	}
	RightPreOrderTra(T->right,T->left);
	return 0;
}

int Destroy(RBtree* T){
	if(*T == NULL){
		return -1;
	}
	RightPostOrderTra((*T)->right, (*T)->left);
	free((*T)->left);
	free((*T));
	*T = NULL;
	return 0;
}

static void RightInOrderTra(RBtree ptr,RBtree NullNode){
	if(ptr != NullNode){
		RightInOrderTra(ptr->left,NullNode);
		printf("% 3d",ptr->data);
		RightInOrderTra(ptr->right,NullNode);
	}
}

static void RightPreOrderTra(RBtree ptr,RBtree NullNode){
	if(ptr != NullNode){
		printf("%3d:%c(%3d,%3d)\n",
			   ptr->data,ptr->color == Red? 'R':'B',
			   ptr->left == NullNode?-1:ptr->left->data,
			   ptr->right == NullNode?-1 :ptr->right->data
			  );
		RightPreOrderTra(ptr->left,NullNode);
		RightPreOrderTra(ptr->right,NullNode);
	}
}

static void RightPostOrderTra(RBtree ptr,RBtree NullNode){
	if(ptr != NullNode){
		RightPostOrderTra(ptr->left,NullNode);
		RightPostOrderTra(ptr->right,NullNode);
		free(ptr);
	}
}

static int Init(RBtree* T){
	Node* tmp;
	tmp = (Node*)malloc(sizeof(Node));
	*T = (Node*)malloc(sizeof(Node));
	if(*T == NULL || tmp == NULL){
		return -1;
	}
	(*T)->data = INT_MIN;
	(*T)->color = Black;
	(*T)->left = (*T)->right = tmp;
	tmp->color = Black;
	tmp->left = tmp->right = tmp;
	return 0;
}

static void RightRotate(RBtree* T){
	Node* Parent = (*T);
	Node* LeftSon = (*T)->left;
	Parent->left = LeftSon->right;
	LeftSon->right = Parent;
	*T = LeftSon;
}

static void LeftRotate(RBtree* T){
	Node* Parent = (*T);
	Node* RightSon = (*T)->right;
	Parent->right = RightSon->left;
	RightSon->left = Parent;
	*T = RightSon;
}
static int FindMin(Node* ptr,RBtree NullNode){
	while(ptr->left != NullNode){
		ptr = ptr->left;
	}
	return ptr->data;
}