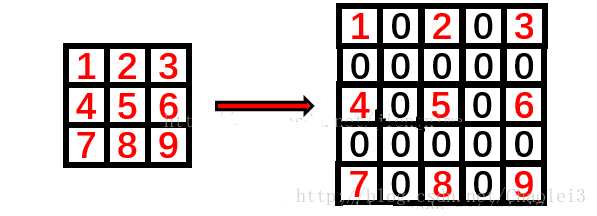
一些算子及不同类型的卷积

1、什么是算子及不同算子的介绍

　　算子是一个函数空间到函数空间上的映射O：X→X。广义上的算子可以推广到任何空间，如内积空间等。

　　在图像处理中，通常会使用一些不同的算子来对图像进行处理。下面介绍一下图像处理中常用的一些算子。

1.相关算子（Correlation Operator)

　　相关算子的表达方法是

\[{\rm{g}} = f \otimes h\]

　　其具体公式为

\[g(i,j) = \sum\limits_{k,l} {f(i + k,j + l)h(k,l)} \]

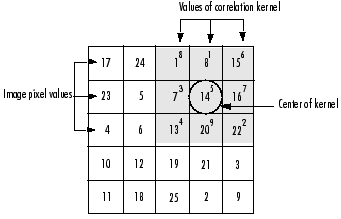
运算步骤为：

1）滑动核，使其中心位于输入图像g的（i，j）像素上

2）利用上式求和，得到输出图像的（i，j）像素值

3）充分上面操纵，直到求出输出图像的所有像素值

例：

　　假设

\[{\rm{a}} = \left( {\begin{array}{*{20}{c}}
{17}&{24}&1&{\begin{array}{*{20}{c}}
8&{15}
\end{array}}\\
{23}&5&7&{\begin{array}{*{20}{c}}
{14}&{16}
\end{array}}\\
4&6&{13}&{\begin{array}{*{20}{c}}
{20}&{22}
\end{array}}\\
{\begin{array}{*{20}{c}}
{10}\\
{11}
\end{array}}&{\begin{array}{*{20}{c}}
{12}\\
{18}
\end{array}}&{\begin{array}{*{20}{c}}
{19}\\
{25}
\end{array}}&{\begin{array}{*{20}{c}}
{\begin{array}{*{20}{c}}
{21}\\
2
\end{array}}&{\begin{array}{*{20}{c}}
3\\
9
\end{array}}
\end{array}}
\end{array}} \right)h = \left( {\begin{array}{*{20}{c}}
8&1&6\\
3&5&7\\
4&9&2
\end{array}} \right)\]

 

Matlab 函数：imfilter(A,h)

　那么计算输出图像的（2，4）元素=

 

2.卷积算子（Convolution)

　　卷积算子的表达方法是

\[g = f*h\]

 　其具体公式为

\[g(i,j) = \sum\limits_{k,l} {f(i - k,j - l)h(k,l) = } \sum\limits_{k,l} {f(k,l)h(i - k,j - l)} \]

运算步骤为：

1）将核围绕中心旋转180度

2）滑动核，使其中心位于输入图像g的（i，j）像素上

3）利用上式求和，得到输出图像的（i，j）像素值

4）充分上面操纵，直到求出输出图像的所有像素值

　　　　将上例中的数据做卷积算子运算为：

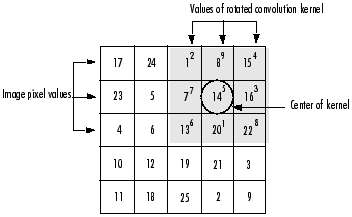Matlab 函数：Matlab 函数：imfilter(A,h,'conv')% imfilter默认是相关算子，因此当进行卷积计算时需要传入参数'conv'

　　那么计算输出图像的（2，4）元素=

 

3.边缘效应

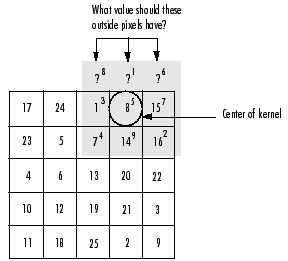
当对图像边缘的进行滤波时，核的一部分会位于图像边缘外面。

常用的策略包括：

1）使用常数填充：imfilter默认用0填充，这会造成处理后的图像边缘是黑色的。

 

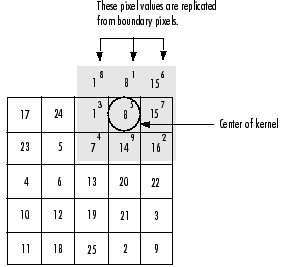
2）复制边缘像素：I3 = imfilter(I,h,'replicate');

4.常用滤波

fspecial函数可以生成几种定义好的滤波器的相关算子的核。

例：unsharp masking 滤波

1 2 3 4 5

I = imread('moon.tif'); h = fspecial('unsharp'); I2 = imfilter(I,h); imshow(I), title('Original Image') figure, imshow(I2), title('Filtered Image')

 

 

5、在图像处理中卷积的计算（注意，下面蓝色矩阵周围有一圈灰色的框，那些就是上面所说到边缘效应）

这里的蓝色矩阵就是输入的图像，粉色矩阵就是卷积层的神经元，这里表示了有两个神经元（w0,w1）。绿色矩阵就是经过卷积运算后的输出矩阵，这里的步长设置为2。

 

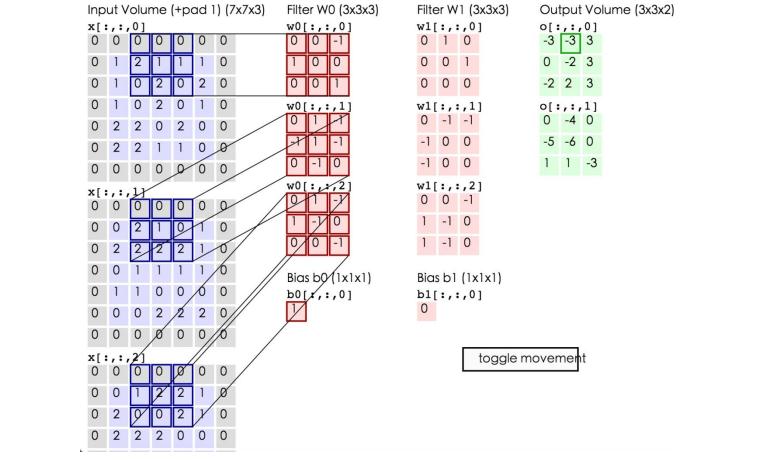
蓝色的矩阵(输入图像)对粉色的矩阵（filter）进行矩阵内积计算并将三个内积运算的结果与偏置值b相加（比如上面图的计算：2+（-2+1-2）+（1-2-2） + 1= 2 - 3 - 3 + 1 = -3），计算后的值就是绿框矩阵的一个元素。

 

下面的动态图形象地展示了卷积层的计算过程：

 

 

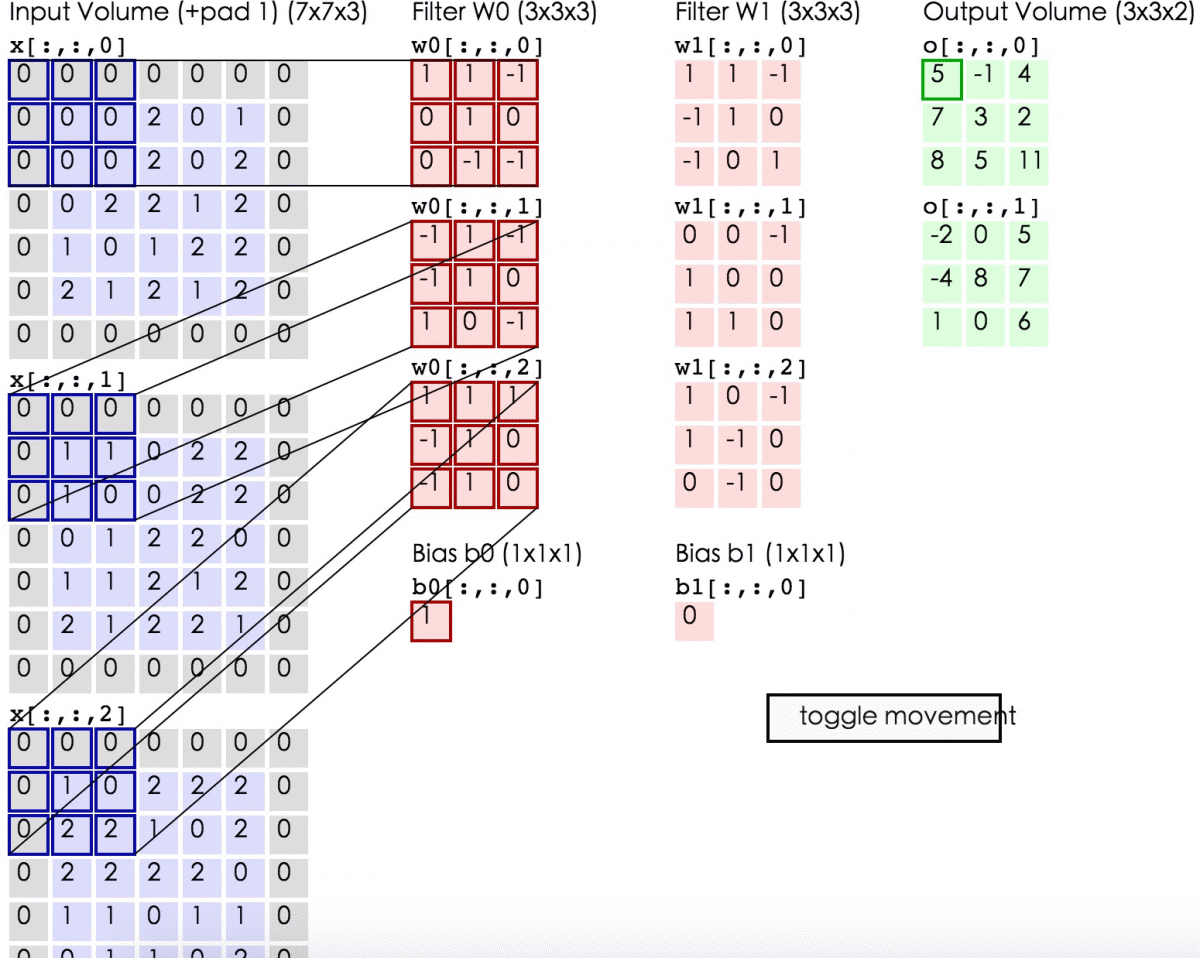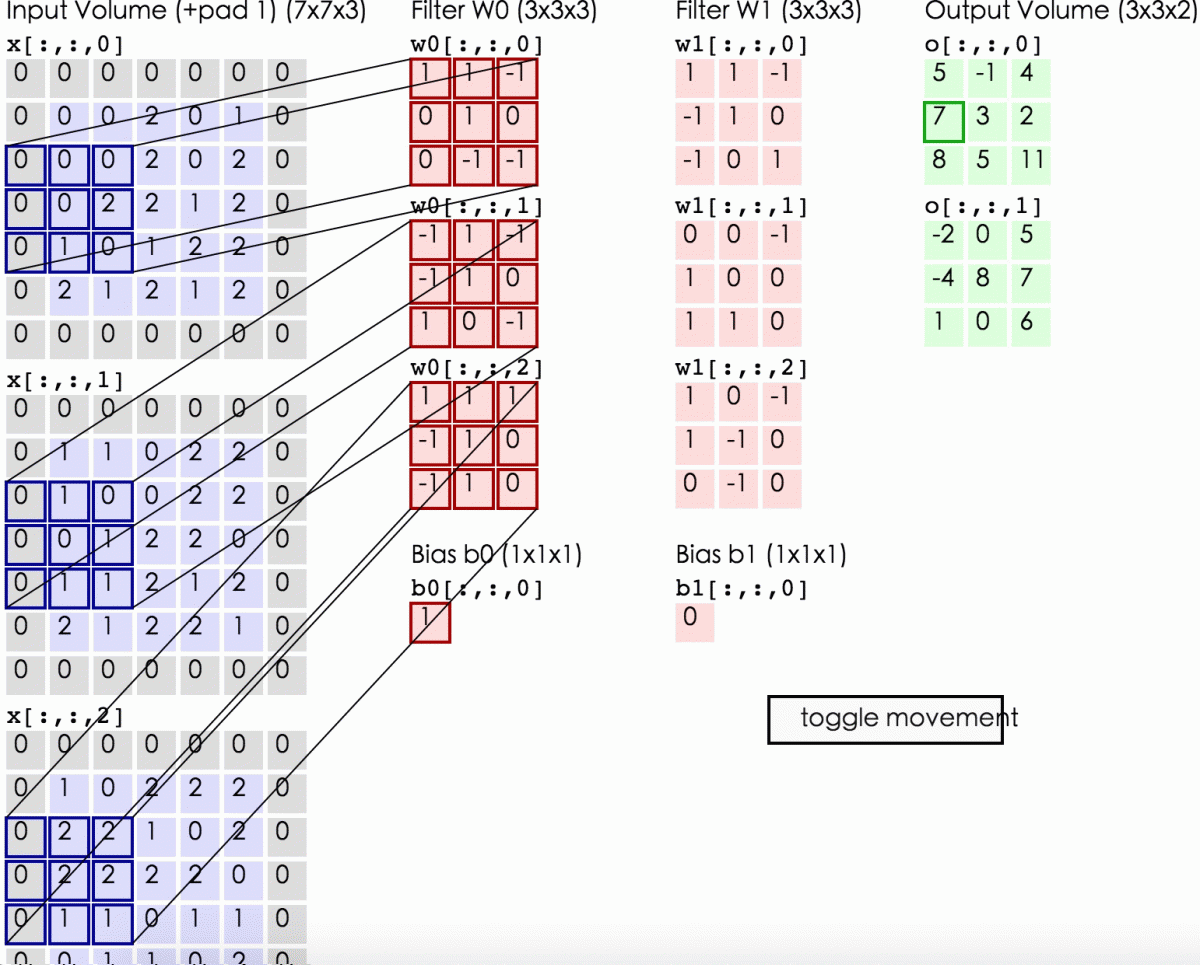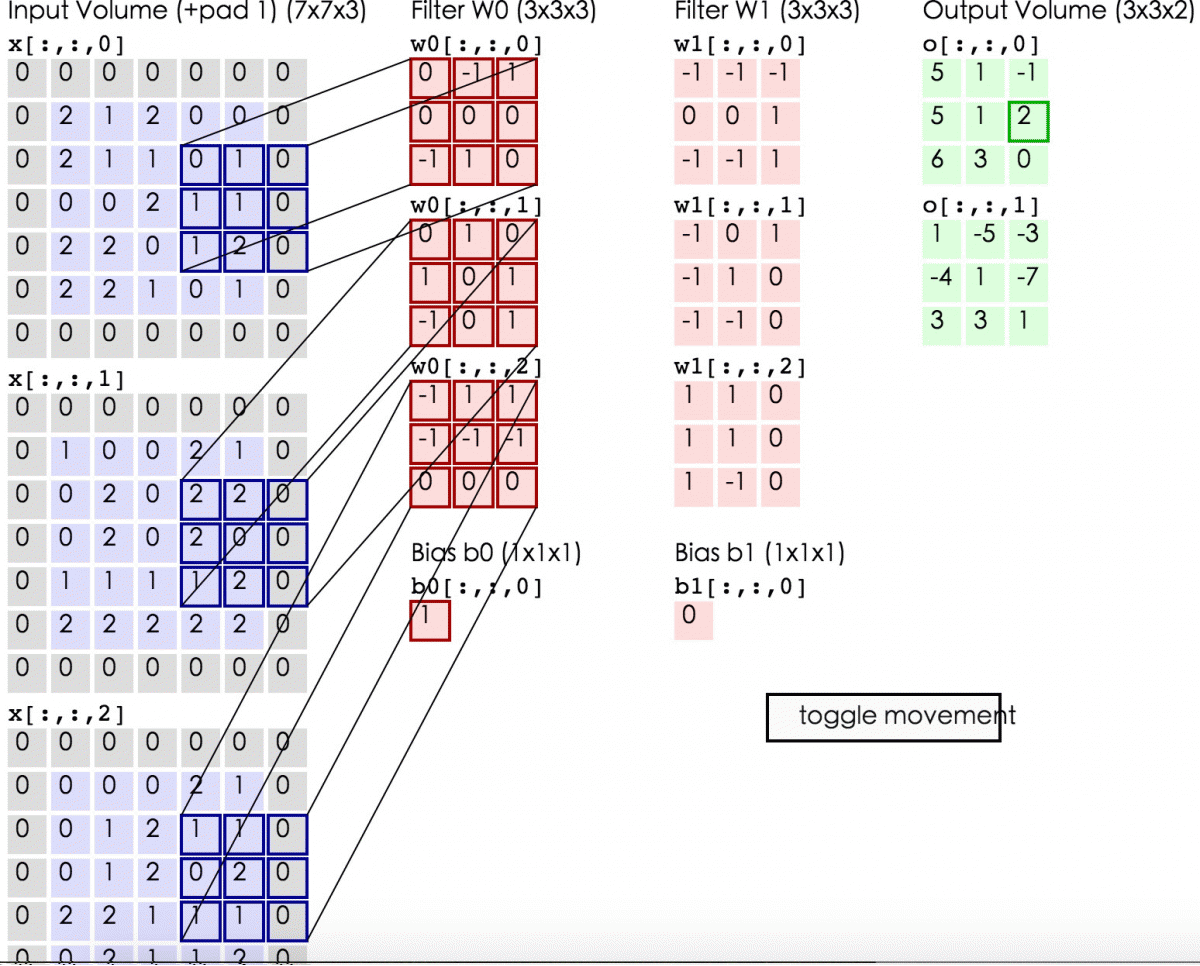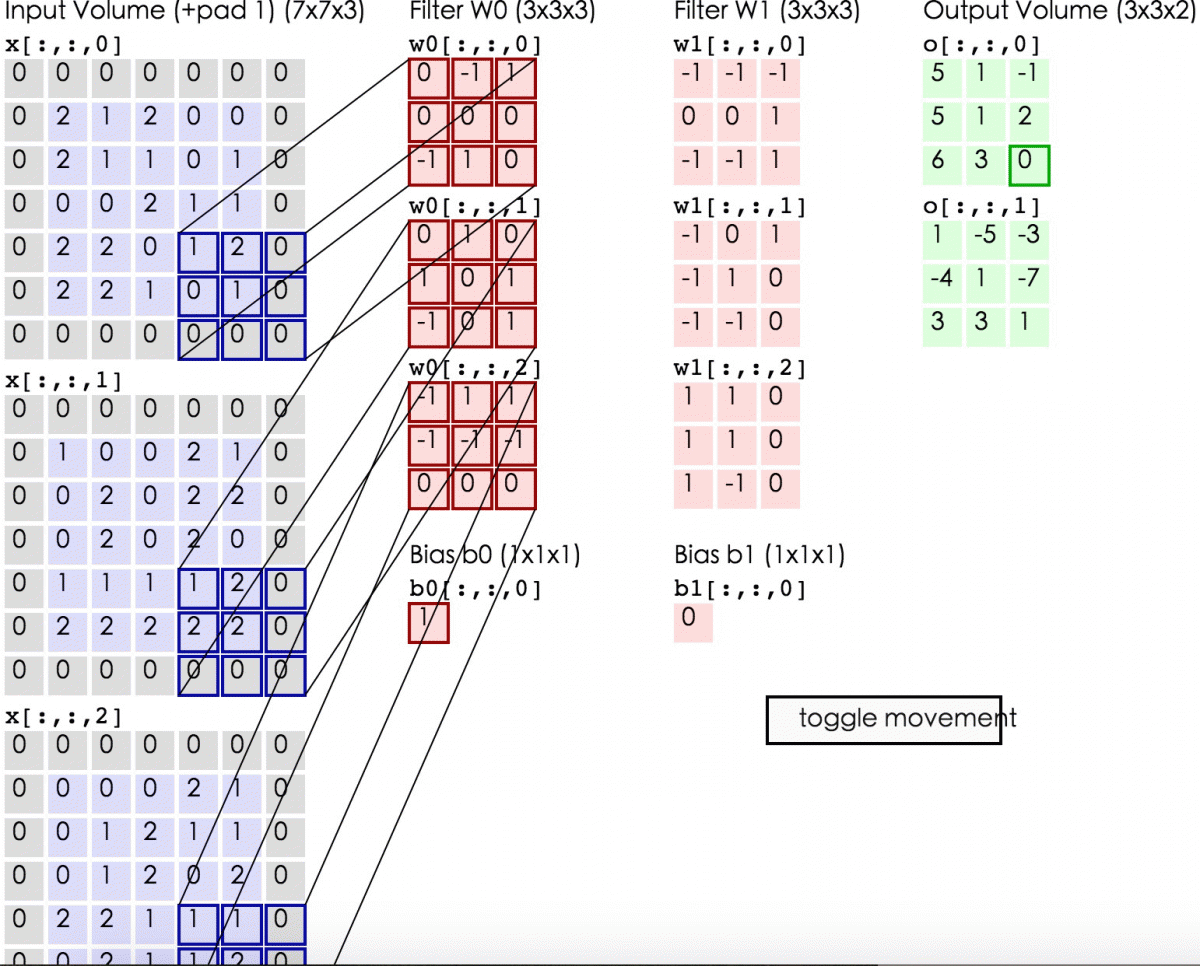
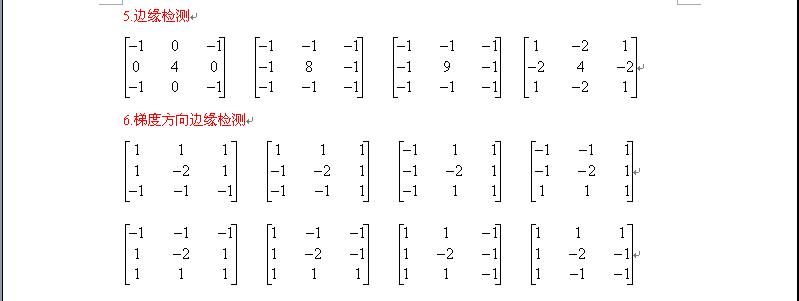
6、在图像处理中常用到的卷积核

 　　了解了卷积在图像处理中的应用形式核方法后，下面是一些在图像处理中常用到的模板（卷积核）

 

7、sobel在图像处理进行边沿检测

　　边缘检测常常借助于空域微分算子进行,通过将其模板与图像卷积完成.主要有一次微分(Sobel算子、Robert算子)、二次微分(Laplacian算子)等。在梯度法的基础上,Sobel提出了一种强方向差分运算与局部平均相结合的方法,即Sobel算子.

 

　　sobel算子的思想，Sobel算子认为，邻域的像素对当前像素产生的影响不是等价的，所以距离不同的像素具有不同的权值，对算子结果产生的影响也不同。一般来说，距离越远，产生的影响越小。其基本思想是，以待增强图像的任意像素(i,j)为中心，截取一个3*3像素的窗口，如下式所示：

\[\begin{array}{*{20}{c}}
{{\rm{f}}(i - 1,j - 1)}&{{\rm{f}}(i - 1,j)}&{{\rm{f}}(i - 1,j + 1)}\\
{{\rm{f}}(i,j - 1)}&{{\rm{f}}(i,j)}&{{\rm{f}}(i,j + 1)}\\
{{\rm{f}}(i + 1,j + 1)}&{{\rm{f}}(i + 1,j)}&{{\rm{f}}(i + 1,j + 1)}
\end{array}\]

 　　分别计算中心像素在x,y方向上的梯度

　　　　

 

 

　　sobel算子的原理，对传进来的图像像素做卷积，卷积的实质是在求梯度值，或者说给了一个加权平均，其中权值就是所谓的卷积核；然后对生成的新像素灰度值做阈值运算，以此来确定边缘信息。

Gx是对原图x方向上的卷积，Gy是对原图y方向上的卷积；

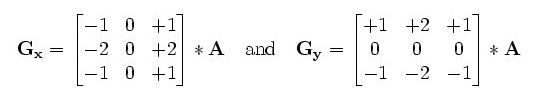
原图中的作用点像素值通过卷积之后为：

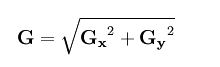
可以简化成：

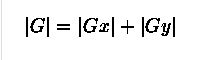
比如，一下矩阵为原图中的像素点矩阵，带入上式中的A，最终得到的G或者|G|是下面(x,y)处的像素值，可以自己去搜索下卷积的含义来理解。

 

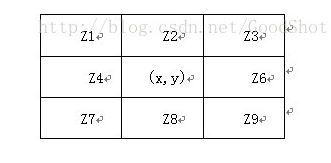
另外，卷积核也可以旋转，用与查找不与x,y轴平行或垂直的方向上的边缘。

 

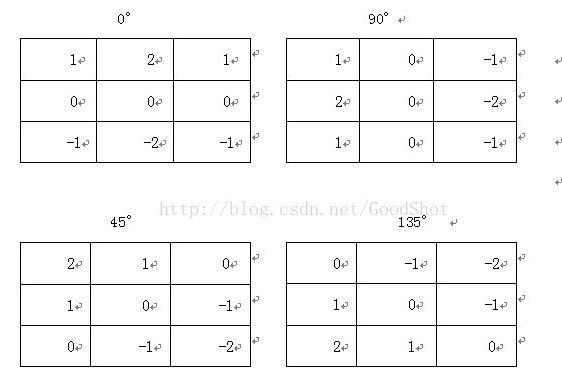
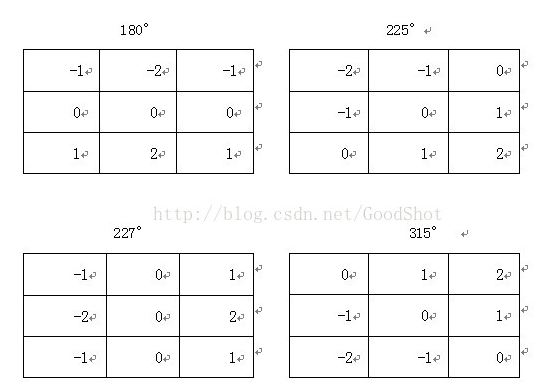
得到像素点新的像素值之后，给定一个阈值就可以得到sobel算子计算出的图像边缘了。

通常，为了消除噪声对sobel算子的影响，会增加一个预处理的操作，主要是做平滑处理降低噪声的影响。

 

下面是其MATLAB的实现及效果图

f=imread('1.jpg');
f=rgb2gray(f);%转化成灰度图
f=im2double(f);%函数im2double 将其值归一化到0～1之间
%使用垂直Sobcl箅子．自动选择阈值
[VSFAT Threshold]=edge(f, 'sobel','vertical'); %边缘探测
figure,imshow(f),title(' 原始图像，');%显示原始图像
figure,imshow(VSFAT),title( '垂直图像边缘检测');
%显示边缘探测图像
%使用水平和垂直Sobel算子，自动选择阈值
SFST=edge(f,'sobel',Threshold);
figure,imshow(SFST),title('水平和垂直图像边缘检测');
%显示边缘探测图像
%使用指定45度角Sobel算子滤波器，指定阂值
s45=[-2 -1 0;-1 0 1;0 1 2];
SFST45=imfilter(f,s45,'replicate');%功能：对任意类型数组或多维图像进行滤波。
SFST45=SFST45>=Threshold;
figure,imshow(SFST45),title('45度角图像边缘检测') ;
%显示边缘探测图像

　　

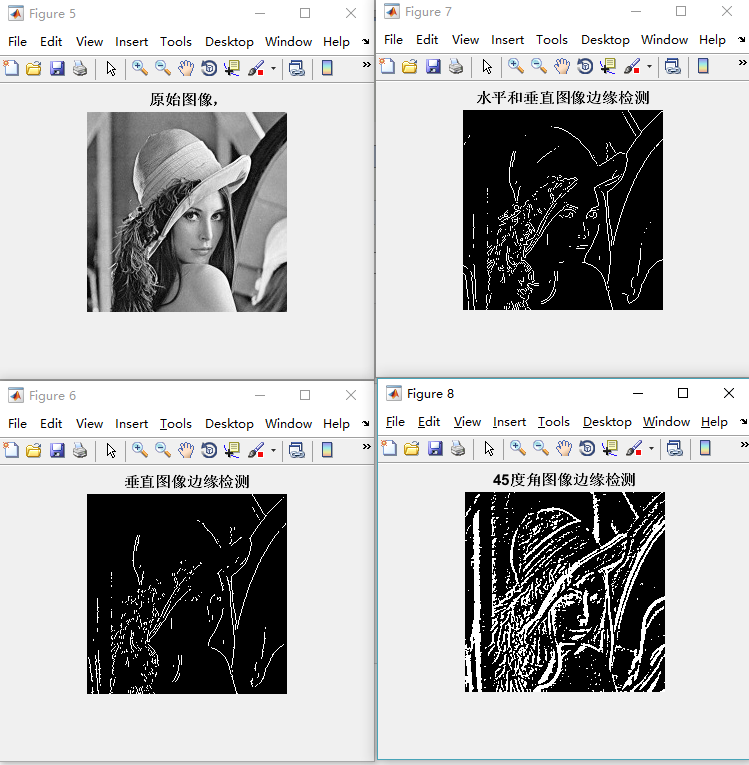
相关的C++代码实现为：

#include "core/core.hpp"   
#include "highgui/highgui.hpp"   
#include "imgproc/imgproc.hpp"   
#include "iostream" 
 
using namespace std;
using namespace cv;
 
int main(int argc, char *argv[])
{
    Mat image = imread("qiaoba.jpg", 0);
    Mat imageX = Mat::zeros(image.size(), CV_16SC1);
    Mat imageY = Mat::zeros(image.size(), CV_16SC1);
    Mat imageXY = Mat::zeros(image.size(), CV_16SC1);
    Mat imageX8UC;
    Mat imageY8UC;
    Mat imageXY8UC;
    if (!image.data)
    {
        return -1;
    }
    GaussianBlur(image, image, Size(3, 3), 0); //高斯滤波消除噪点 
    uchar *P = image.data;
    uchar *PX = imageX.data;
    uchar *PY = imageY.data;
    int step = image.step;
    int stepXY = imageX.step;
    for (int i = 1; i<image.rows - 1; i++)
    {
        for (int j = 1; j<image.cols - 1; j++)
        {
            //通过指针遍历图像上每一个像素 
            PX[i*imageX.step + j*(stepXY / step)] = abs(P[(i - 1)*step + j + 1] + P[i*step + j + 1] * 2 + P[(i + 1)*step + j + 1] - P[(i - 1)*step + j - 1] - P[i*step + j - 1] * 2 - P[(i + 1)*step + j - 1]);
            PY[i*imageX.step + j*(stepXY / step)] = abs(P[(i + 1)*step + j - 1] + P[(i + 1)*step + j] * 2 + P[(i + 1)*step + j + 1] - P[(i - 1)*step + j - 1] - P[(i - 1)*step + j] * 2 - P[(i - 1)*step + j + 1]);
        }
    }
    addWeighted(imageX, 0.5, imageY, 0.5, 0, imageXY);//融合X、Y方向   
    convertScaleAbs(imageX, imageX8UC);
    convertScaleAbs(imageY, imageY8UC);
    convertScaleAbs(imageXY, imageXY8UC);   //转换为8bit图像 
 
    Mat imageSobel;
    Sobel(image, imageSobel, CV_8UC1, 1, 1); //Opencv的Sobel函数 
 
    imshow("Source Image", image);
    imshow("X Direction", imageX8UC);
    imshow("Y Direction", imageY8UC);
    imshow("XY Direction", imageXY8UC);
    imshow("Opencv Soble", imageSobel);
    waitKey();
    return 0;
}

　　

 

sobel的优缺点也比较明确。

优点：计算简单，速度很快；

缺点：计算方向单一，对复杂纹理的情况显得乏力；

　　直接用阈值来判断边缘点欠合理解释，会造成较多的噪声点误判。

 

 

 

 

 

 

2、对深度可分离卷积、分组卷积、扩张卷积、转置卷积（反卷积）的理解

　　前面讲解了卷积的原理，及卷积在图像中的基础应用，但是在实际应用中，根据需求和硬件条件的不同，卷积的应用方法和名称也不同。这里有必要将一些常用的卷积拿出来单独讲一下。不过在介绍前需要了解一些在深度学习中卷积的基本结构的定义：

卷积核大小（Kernel Size）：定义了卷积操作的感受野。在二维卷积中，通常设置为3，即卷积核大小为3×3。

步幅（Stride）：定义了卷积核遍历图像时的步幅大小。其默认值通常设置为1，也可将步幅设置为2后对图像进行下采样，这种方式与最大池化类似。

边界扩充（Padding）：定义了网络层处理样本边界的方式。当卷积核大于1且不进行边界扩充，输出尺寸将相应缩小；当卷积核以标准方式进行边界扩充，则输出数据的空间尺寸将与输入相等。

输入与输出通道（Channels）：构建卷积层时需定义输入通道I，并由此确定输出通道O。这样，可算出每个网络层的参数量为I×O×K，其中K为卷积核的参数个数。例，某个网络层有64个大小为3×3的卷积核，则对应K值为 3×3 =9。

1、深度可分离卷积

 　　　在可分离卷积（separable convolution）中，通常将卷积操作拆分成多个步骤。而在神经网络中通常使用的就是深度可分离卷积（depthwise separable convolution）。 

　　假设有一个3×3大小的卷积层，其输入通道为16、输出通道为32。那么一般的操作就是用32个3×3的卷积核来分别同输入数据卷积，这样每个卷积核需要3×3×16个参数，得到的输出是只有一个通道的数据。之所以会得到一通道的数据，是因为刚开始3×3×16的卷积核的每个通道会在输入数据的每个对应通道上做卷积，然后叠加每一个通道对应位置的值，使之变成了单通道，那么32个卷积核一共需要(3×3×16)×32 =4068个参数。

　　用一张来解释深度可分离卷积，如下：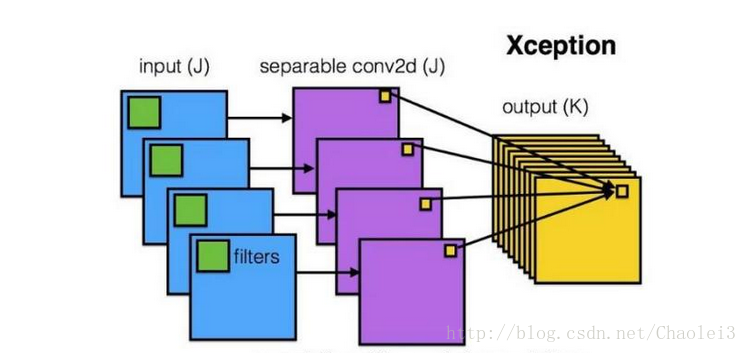 
 

可以看到每一个通道用一个filter卷积之后得到对应一个通道的输出，然后再进行信息的融合。而以往标准的卷积过程可以用下面的图来表示： 

 

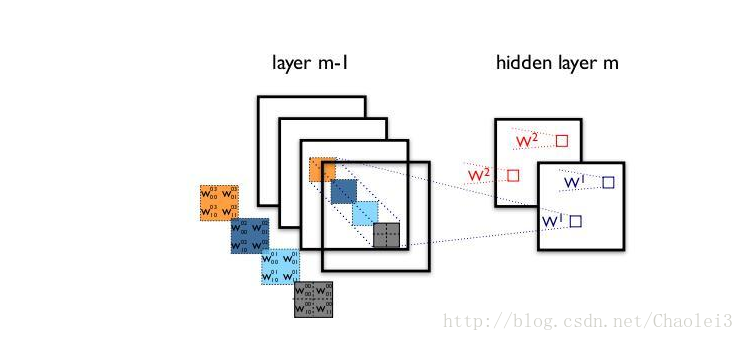
　　而应用深度可分离卷积的过程是①用16个3×3大小的卷积核（1通道）分别与输入的16通道的数据做卷积（这里使用了16个1通道的卷积核，输入数据的每个通道用1个3×3的卷积核卷积），得到了16个通道的特征图，我们说该步操作是depthwise（逐层）的，在叠加16个特征图之前，②接着用32个1×1大小的卷积核（16通道）在这16个特征图进行卷积运算，将16个通道的信息进行融合（用1×1的卷积进行不同通道间的信息融合），我们说该步操作是pointwise（逐像素）的。这样我们可以算出整个过程使用了3×3×16+（1×1×16）×32 =656个参数。可以看出运用深度可分离卷积比普通卷积减少了所需要的参数。重要的是深度可分离卷积将以往普通卷积操作同时考虑通道和区域改变成，卷积先只考虑区域，然后再考虑通道。实现了通道和区域的分离。

2、分组卷积

　　Group convolution 分组卷积，最早在AlexNet中出现，由于当时的硬件资源有限，训练AlexNet时卷积操作不能全部放在同一个GPU处理，因此作者把feature maps分给多个GPU分别进行处理，最后把多个GPU的结果进行融合。

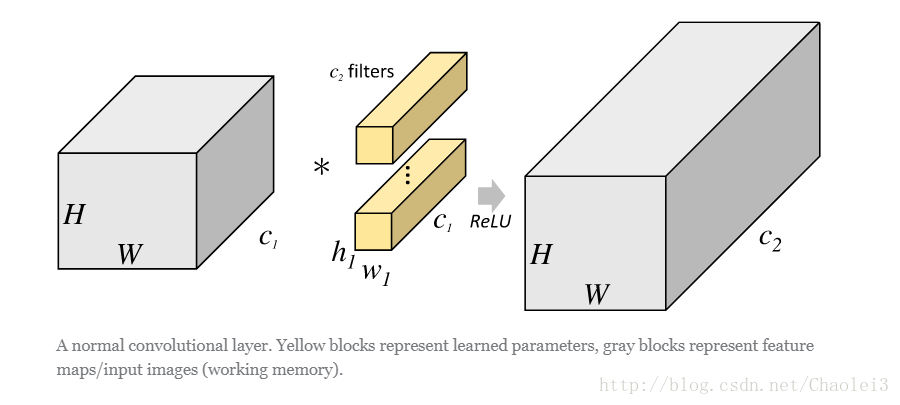
　　在说明分组卷积之前我们用一张图来体会一下一般的卷积操作。 

　　从上图可以看出，一般的卷积会对输入数据的整体一起做卷积操作，即输入数据：H1×W1×C1；而卷积核大小为h1×w1，一共有C2个，然后卷积得到的输出数据就是H2×W2×C2。这里我们假设输出和输出的分辨率是不变的。主要看这个过程是一气呵成的，这对于存储器的容量提出了更高的要求。 
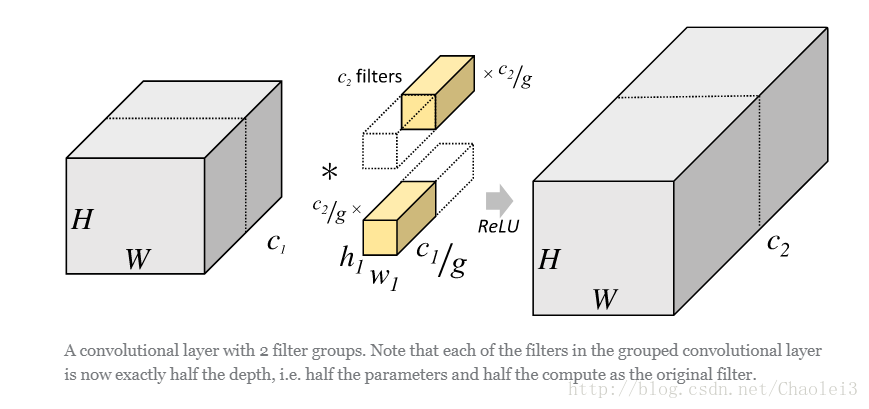
但是分组卷积明显就没有那么多的参数。先用图片直观地感受一下分组卷积的过程。对于上面所说的同样的一个问题，分组卷积就如下图所示。 

　　可以看到，图中将输入数据分成了2组（组数为g），需要注意的是，这种分组只是在深度上进行划分，即某几个通道编为一组，这个具体的数量由（C1/g）决定。因为输出数据的改变，相应的，卷积核也需要做出同样的改变。即每组中卷积核的深度也就变成了（C1/g），而卷积核的大小是不需要改变的，此时每组的卷积核的个数就变成了（C2/g）个，而不是原来的C2了。然后用每组的卷积核同它们对应组内的输入数据卷积，得到了输出数据以后，再用concatenate的方式组合起来，最终的输出数据的通道仍旧是C2。也就是说，分组数g决定以后，那么我们将并行的运算g个相同的卷积过程，每个过程里（每组），输入数据为H1×W1×C1/g，卷积核大小为h1×w1×C1/g，一共有C2/g个，输出数据为H2×W2×C2/g。

　　从一个具体的例子来看，Group conv本身就极大地减少了参数。比如当输入通道为256，输出通道也为256，kernel size为3×3，不做Group conv参数为256×3×3×256。实施分组卷积时，若group为8，每个group的input channel和output channel均为32，参数为8×32×3×3×32，是原来的八分之一。而Group conv最后每一组输出的feature maps应该是以concatenate的方式组合。 
Alex认为group conv的方式能够增加 filter之间的对角相关性，而且能够减少训练参数，不容易过拟合，这类似于正则的效果。

 

3、空洞（扩张）卷积（Dilated/Atrous Convolution）

　　空洞卷积（dilated convolution）是针对图像语义分割问题中下采样会降低图像分辨率、丢失信息而提出的一种卷积思路。利用添加空洞扩大感受野，让原本3 
x3的卷积核，在相同参数量和计算量下拥有5x5（dilated rate =2）或者更大的感受野，从而无需下采样。扩张卷积（dilated convolutions）又名空洞卷积（atrous convolutions），向卷积层引入了一个称为 “扩张率(dilation rate)”的新参数，该参数定义了卷积核处理数据时各值的间距。换句话说，相比原来的标准卷积，扩张卷积（dilated convolution） 多了一个hyper-parameter（超参数）称之为dilation rate（扩张率），指的是kernel各点之前的间隔数量，【正常的convolution 的 dilatation rate为 1】。

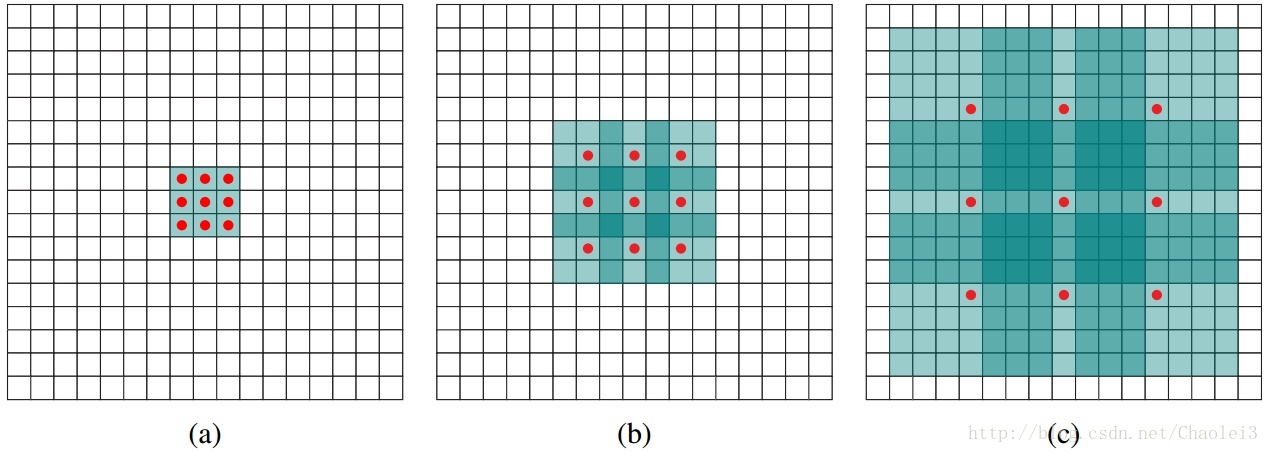
图说空洞卷积的概念

(a)图对应3x3的1-dilated conv，和普通的卷积操作一样。(b)图对应3x3的2-dilated conv，实际的卷积kernel size还是3x3，但是空洞为1，需要注意的是空洞的位置全填进去0，填入0之后再卷积即可。【此变化见下图】（c）图是4-dilated conv操作。 
在上图中扩张卷积的感受野可以由以下公式计算得到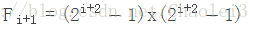；其中i+1表示dilated rate。 
比如上图中（a），dilated=1，F(dilated) = 3×3；图（b）中，dilated=2，F(dilated)=7×7；图（c）中，dilated=4， F(dilated)=15×15。 
dilated=2时具体的操作，即按照下图在空洞位置填入0之后，然后直接卷积就可以了。 

空洞卷积的动态过程

在二维图像上直观地感受一下扩张卷积的过程： 
 
上图是一个扩张率为2的3×3卷积核，感受野与5×5的卷积核相同，而且仅需要9个参数。你可以把它想象成一个5×5的卷积核，每隔一行或一列删除一行或一列。 
在相同的计算条件下，空洞卷积提供了更大的感受野。空洞卷积经常用在实时图像分割中。当网络层需要较大的感受野，但计算资源有限而无法提高卷积核数量或大小时，可以考虑空洞卷积。

Dilated Convolution感受野指数级增长

对于标准卷积核情况，比如用3×3卷积核连续卷积2次，在第3层中得到1个Feature点，那么第3层这个Feature点换算回第1层覆盖了多少个Feature点呢？ 
第3层： 

 
第2层：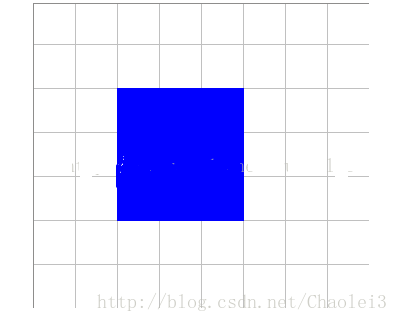 
 
第1层：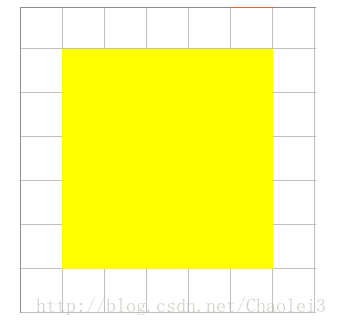 
 

第一层的一个5×5大小的区域经过2次3×3的标准卷积之后，变成了一个点。也就是说从size上来讲，2层3*3卷积转换相当于1层5*5卷积。题外话，从以上图的演化也可以看出，一个5×5的卷积核是可以由2次连续的3×3的卷积代替。 
但对于dilated=2，3*3的扩张卷积核呢？ 
第3层的一个点： 

 
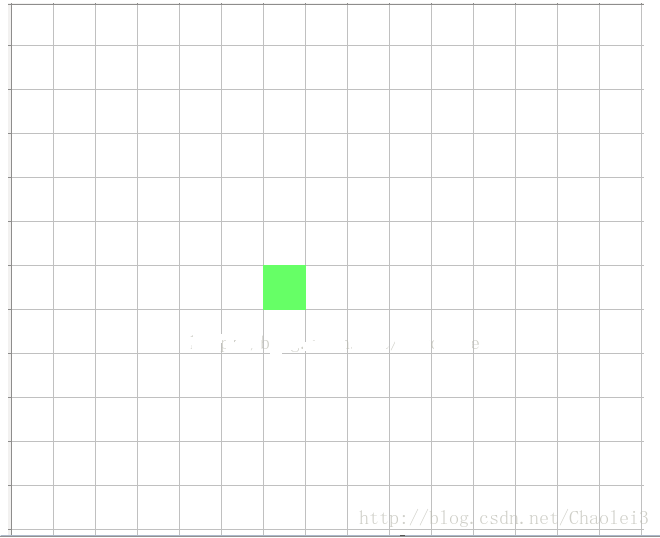
第2层： 
 
 

可以看到第一层13×13的区域，经过2次3×3的扩张卷积之后，变成了一个点。即从size上来讲，连续2层的3×3空洞卷积转换相当于1层13×13卷积。

 

转置卷积和反卷积的区别

那什么是反卷积？从字面上理解就是卷积的逆过程。值得注意的反卷积虽然存在，但是在深度学习中并不常用。而转置卷积虽然又名反卷积，却不是真正意义上的反卷积。因为根据反卷积的数学含义，通过反卷积可以将通过卷积的输出信号，完全还原输入信号。而事实是，转置卷积只能还原shape大小，而不能还原value。你可以理解成，至少在数值方面上，转置卷积不能实现卷积操作的逆过程。所以说转置卷积与真正的反卷积有点相似，因为两者产生了相同的空间分辨率。但是又名反卷积（deconvolutions）的这种叫法是不合适的，因为它不符合反卷积的概念。

转置卷积的动态图

 

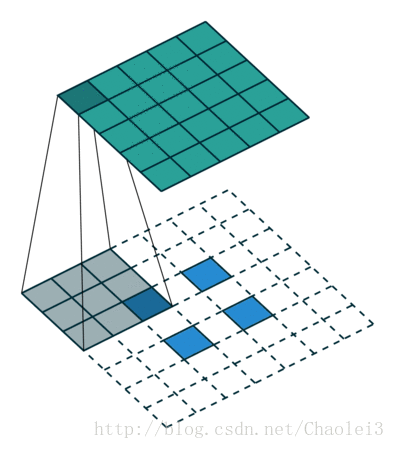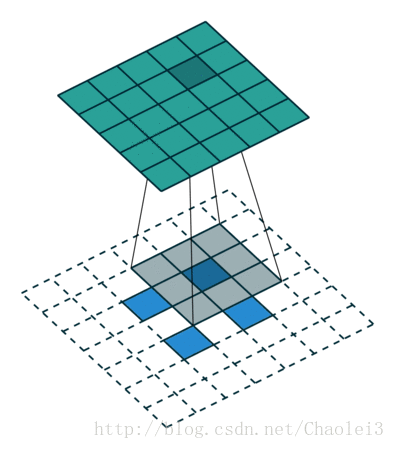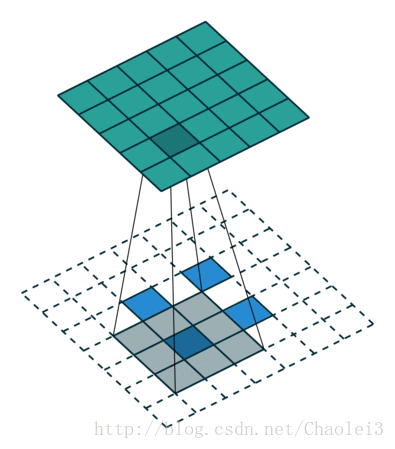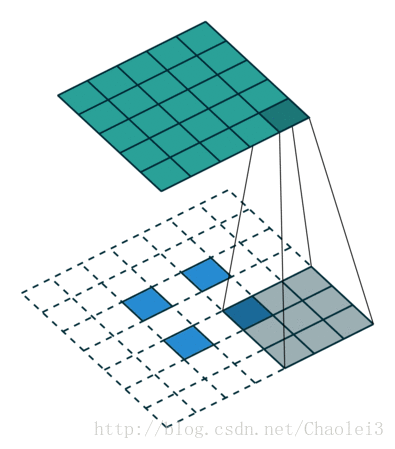
△卷积核为3×3、步幅为2和无边界扩充的二维转置卷积 
需要注意的是，转置前后padding，stride仍然是卷积过程指定的数值，不会改变。

例子

由于上面只是理论的说明了转置卷积的目的，而并没有说明如何由卷积之后的输出重建输入。下面我们通过一个例子来说明感受下。 
比如有输入数据：3×3，Reshape之后，为A ：1×9，B(可以理解为滤波器)：9×4(Toeplitz matrix) 那么A*B=C：1×4；Reshape C=2×2。所以，通过B 卷积，我们从输入数据由shape=3×3变成了shape=2×2。反过来。当我们把卷积的结果拿来做输入，此时A：2×2,reshape之后为1×4，B的转置为4×9，那么A*B=C=1×9，注意此时求得的C，我们就认为它是卷积之前的输入了，虽然存在偏差。然后reshape为3×3。所以，通过B的转置 - “反卷积”，我们从卷积结果shape=2×2得到了shape=3×3，重建了分辨率。 
也就是输入feature map A=[3,3]经过了卷积B=[2,2] 输出为 [2,2] ,其中padding=0,stride=1，反卷积（转置卷积）则是输入feature map A=[2,2],经过了反卷积滤波B=[2,2].输出为[3,3]。其中padding=0,stride=1不变。那么[2,2]的卷积核(滤波器)是怎么转化为[4,9]或者[9,4]的呢？通过Toeplitz matrix。 
至于这其中Toeplitz matrix是个什么东西，此处限于篇幅就不再介绍了。但即使不知道这个矩阵，转置卷积的具体工作也应该能够明白的。

 

 

 

 

参考资料： 

https://blog.csdn.net/chaolei3/article/details/79374563
https://zhuanlan.zhihu.com/p/28749411 
https://zhuanlan.zhihu.com/p/28186857 
https://blog.yani.io/filter-group-tutorial/ 
https://www.zhihu.com/question/54149221 
http://blog.csdn.net/guvcolie/article/details/77884530?locationNum=10&fps=1 
http://blog.csdn.net/zizi7/article/details/77369945 
https://github.com/vdumoulin/conv_arithmetic 
https://www.zhihu.com/question/43609045/answer/130868981

https://wenku.baidu.com/view/7218f2e6162ded630b1c59eef8c75fbfc77d94bc.html

sobel算子

图像梯度：算子

 郑南宁,计算机视觉与模式识别[M]国防工业出版社,1998