Pixel3D Spring - 3D粒子爆炸

 

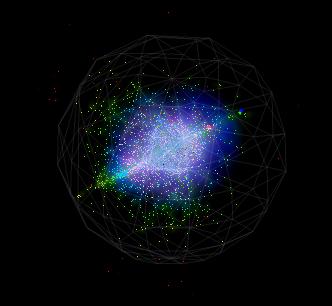
三个带斥力的球体和一个中心引力，带动了所有粒子的变化。

做这个demo花了比较长时间，第一，曾经让我思考了很久的三维球体碰撞反弹算法。十分幸运，我在搜索相关资料的时候，找到一个二维球体碰撞反弹的例子。该例子图文并茂，很好的分析了各种碰撞的情况，并介绍了算法。

如何发散到三维空间里应用呢？突然想起能量守恒定律，似乎粒子在一个理想空间（没有外力作用，没有能量损失）下运动，那么他具有初速度vx0,vy0,vz0，合速度为v0 = vx0^2 + vy0^2 + vz0^2 。在碰撞发生后，利用上述算法求得vx1,vy1后，用Math.sqrt(v0 - vx1^2 - vy1^2)，似乎就得到了vz1。速率有了，方向怎办？我们猜想一下，既然在xy坐标系能够得到碰撞后的vx,vy方向，为何不能在xz坐标系里得到vz的方向呢？答案是肯定的。我们把z轴当作y轴，和上述的算法一样，就容易得到了vz的方向。好了，速率有了，方向有了，目的已经达到。

接下来，第二个让我困扰的问题。我们知道在pv3d里很容易就能创建大量粒子。但可能大部分人都不清楚它是如何创建这些粒子的，我先说明一下。

 

首先创建一个bitmapEffectLayer

var bfx:BitmapEffectLayer = new BitmapEffectLayer(viewport, w, h, true, 0, BitmapClearMode.CLEAR_PRE, true, false);

 

然后创建pixels

var pixels:MotionPixels = new MotionPixels(bfx, box);

for (var i:int = 1; i < 60; i ++)
{
    for (var j:int = 0; j < box.geometry.vertices.length; j++)
    {
        pixels.addPixel3D(new MotionPixel(0xFFFFFFFF, getPos(box.geometry.vertices[j].x, i, 10), getPos(box.geometry.vertices[j].y, i, 10), getPos(box.geometry.vertices[j].z, i, 10)));
    }
}

 

看到这里，为什么要把bfx传到里面呢？有什么作用？原来，当我们在pixels里面添加pixel的时候，会在这个biemap上绘制点。但他不是单纯的按照我们给定的坐标绘制进去，这中间的过程原来相当复杂。现在分析一下这个过程。先来看看3D坐标投影到平面的重点算法公式：fz = focus * zoom / (focus + z)

 

var v:Matrix3D = this.view;
//
var sz:Number = vx * v.n31 + vy * v.n32 + vz * v.n33 + v.n34;
var sx:Number = vx * v.n11 + vy * v.n12 + vz * v.n13 + v.n14;
var sy:Number = vx * v.n21 + vy * v.n22 + vz * v.n23 + v.n24;
var fz:Number = (renderSessionData.camera.focus * renderSessionData.camera.zoom) / (renderSessionData.camera.focus + sz);
                    
v3d.x = sx * fz;
v3d.y = sy * fz;
v3d.z = sz;

 

Matrix3D是一个4x4矩阵，小弟没学好高数，还没搞清楚这东西，见谅 - -! 最后得到的就是真正呈现在这张bitmap上的点的坐标了。

canvas.setPixel32(v3d.x+offsetX, v3d.y+offsetY, p.color);

 

随后的事情就是计算引力和斥力的过程了。这个不多说了，不太难。

 

如果你有更好的想法和建议，欢迎和本人共同讨论。

 

Preview:http://niuniuzhu.cn/p/PixelSprings/