cs229_part7
PCA
问题背景
回顾一下我们特征选择中的问题。如果特征非常多，而且有一些特征是重复的，那么我们可以想办法剔除掉一些无用的特征。那里我们提到一个计算互信息的方法。那么这里换一种降维方法。
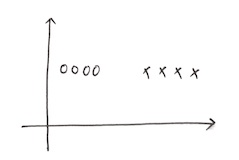
比如说这样的一种比较极端的情况，我们数据是二维的，但是很明显能看的出来有一个维度对于分类是没有任何作用的，那我们可以把这个数据投影到x轴上面，变成这样：
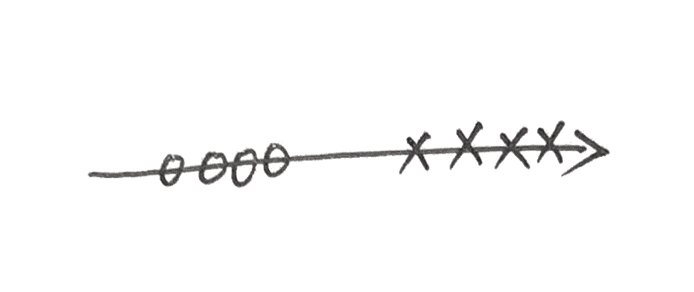
这样我们就把二维的数据降到了一维。
当然这只是一种比较极端的情况，但是对于任意情况也是可以推广的。比如上面这个情况，投到x轴是最好的情况，而投到y轴上是最差的情况。因为投到y轴上就变成了一个点，还怎么分类。
那么主要的想法就是，我们找到一个超平面，然后把特征投到超平面上面，那要怎么投呢，就是投完之后使得点之间的距离越大越好。
形式描述
如果我们的样本在超平面上的投影是\(\mathbf { W } ^ { T } x _ { i }\)那么投影后样本的方差就是\(\sum _ { i } \mathbf { W } ^ { T } x _ { i } x _ { i } ^ { T } \mathbf { W }\)
那么优化目标就是：
\[\left.\begin{array} { c } { \max _ { \mathbf { W } } \operatorname{tr} \left( \mathbf { W } ^ { \text{T} } \mathbf { X } \mathbf { X } ^ { \text{T} } \mathbf { W } \right) } \\ { \mathbf { s .t .} \mathbf { W } ^ { \text{T} } \mathbf { W } = \mathbf { I } } \end{array} \right.
\]
利用拉格朗日算子可得：
\[\mathbf { X } \mathbf { X } ^ { \text{T} } \mathbf { W } = \lambda \mathbf { W }
\]
于是对\(\mathbf { X } \mathbf { X }\)做特征分解取所需要的特征即可。
过程就是：
- 对样本集进行中心化处理：\(x _ { i } \leftarrow x _ { i } - \frac { 1} { m } \sum _ { i = 1} ^ { m } x _ { i }\)
- 计算协方差矩阵：$$\mathbf { X } \mathbf { X }$$
- 对协方差矩阵进行特征分解
- 取最大的d个特征作为所需要的特征向量\(w _ { 1} ,w _ { 2} ,\dots ,w _ { d }\)
- 得到投影矩阵\(\mathbf { W } = \left( w _ { 1} ,w _ { 2} ,\ldots ,w _ { d } \right)\)
如果这个推导过程看不懂的话请翻阅参考。
