cs229_part4

又到了一节很重要的课，因为这个学习理论是从统计角度为机器学习算法提供了一个理论基础。

学习理论

问题背景

先回顾一下我们第一节课提到的机器学习的组成：

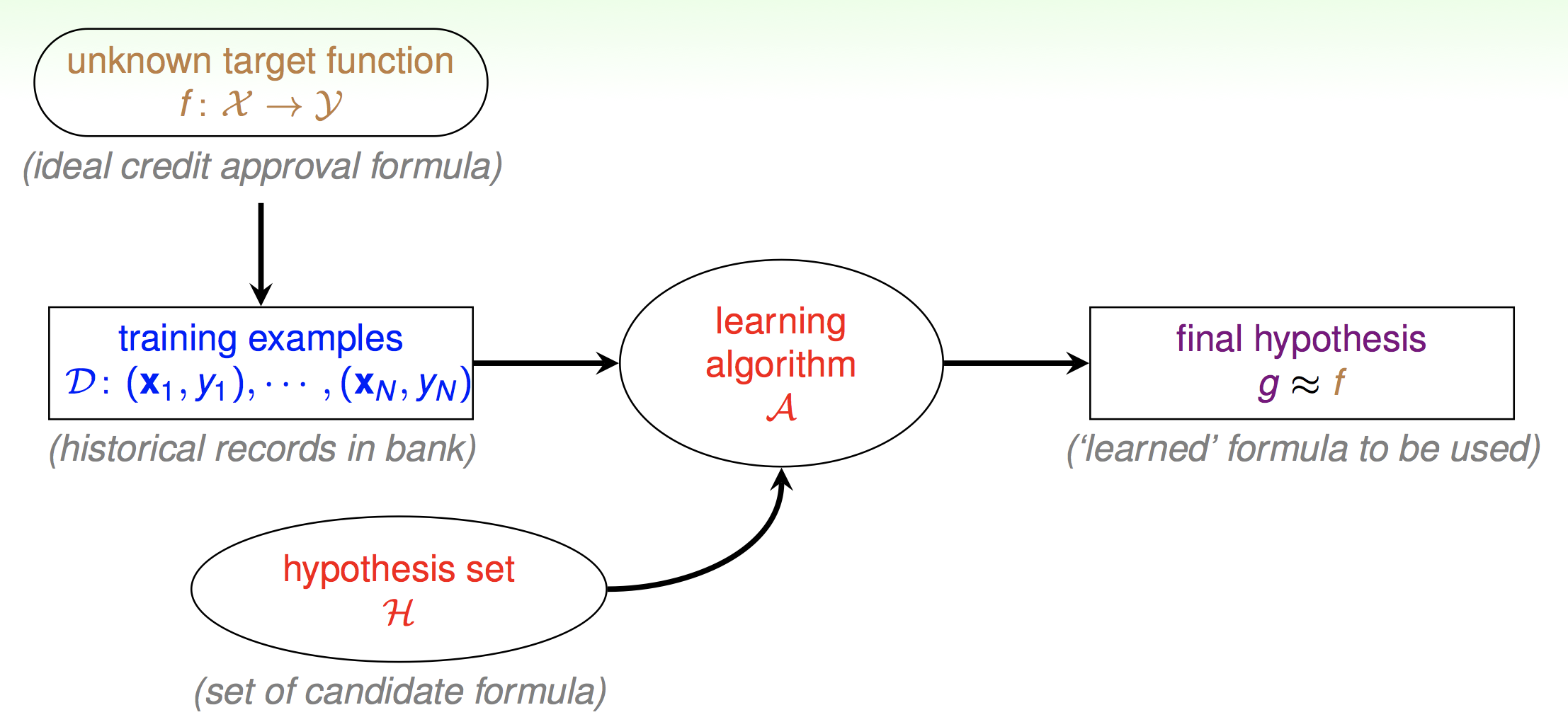
第一节课只是简单的提了一下，现在我们要真正来分析这张图了。首先机器学习的最终目的就是得到真正的映射f，但是f我们无法得到，所以拿一个g去拟合。这是什么意思呢。就比如说你高考，会刷很多的习题，有很多次的模拟考。但是最终最终的目的都是为高考取得一个好成绩。那么这里也是一样的，如果你开始就拿到了高考的考卷，那你还刷什么习题，直接背高考的考卷不就完了吗。但是我们拿不到真实的考卷，所以我们刷习题。但是这里就两个问题了。第一，你模拟考考了600分就代表你高考真的能考600分么。也就是说我们怎么保证我们估计出来的g与真实分布的f相接近呢。第二，我们如何在模拟考中取得好成绩呢。也就是说如何让g表现得尽量好呢。

首先我们先明确一个概念叫泛化误差，也就是我们模型在真实分布下的误差。或者说最终高考的真实成绩。

给定样本集描述：
\((x,y)\in D, x\in R^n, y\in \{0,1\}\)
我们来回归一下基本的机器学习流程。

构造假设

这里以最简单的二分类模型为例，即我们之前提到的感知机算法：

\[h(x)= \begin{cases} +1 & \theta^Tx \ge 0 \\ -1 & \theta^Tx \lt 0 \end{cases} \]

所以假设集也可以表示为

\[\mathcal { H } = \left\{ h _ { \theta } : h _ { \theta } ( x ) = 1\left\{ \theta ^ { T } x \geq 0\right\} ,\theta \in \mathbb { R } ^ { n + 1} \right\} \]

衡量误差

\[\hat { \varepsilon } ( h ) = \frac { 1} { m } \sum _ { i = 1} ^ { m } 1\left\{ h \left( x ^ { ( i ) } \right) \neq y ^ { ( i ) } \right\} \]

那么误差就是在样本中被误分类的点。这个误差我们一般称之为训练误差，或者经验误差，或者经验风险。

那么与经验误差对应的就是泛化误差了：

\[\varepsilon ( h ) = P _ { ( x ,y ) \sim \mathcal { D } } ( h ( x ) \neq y ) \]

求解问题

既然我们没法衡量泛化误差，那么就求经验误差最小，于是得到最终的假设函数的参数就是：

\[\hat { \theta } = \arg \min _ { \theta } \hat { \varepsilon } \left( h _ { \theta } \right) \]

我们一般把这种算法称之为经验风险最小算法。

经验误差与泛化误差的一致性

我们基于现有的数据已经得到最好的模型，那我们怎么确定他在新的数据下也能表现得很好呢。
也就是说我们如何保证经验误差与泛化误差的一致性呢。我们希望这种一致性越高越好。

这里我们给出一条引理：
如果你有m个随机变量Z遵循独立同分布(i.i.d)那么有：

\[\left.\begin{array} { c } { Z _ { 1} ,\ldots ,Z _ { m } ( i .i .d ) \sim \text{ Bernoulli } ( \phi ) } \\ { \hat { \phi } = ( 1/ m ) \sum _ { i = 1} ^ { m } Z _ { i } } \end{array} \right. \]

可以得到Hoeffding不等式：

\[P ( | \phi - \hat { \phi } | > \gamma ) \leq 2\exp \left( - 2\gamma ^ { 2} m \right) \]

这条不等式的正确性基本的概率论书上都有讲。\(\hat\phi\)是一个估计量，\(\phi\)真实参数的值，\(\gamma\)表示置信度。

带入我们的经验误差与泛化误差：

\[P \left( | \varepsilon \left( h _ { i } \right) - \hat { \varepsilon } \left( h _ { i } \right) | > \gamma \right) \leq 2\exp \left( - 2\gamma ^ { 2} m \right) \]

这条公式给出了经验误差与泛化误差的差距的上界。也就是说随着样本数量的增加，经验误差一定会趋向于泛化误差。这相当于给了我们保证，我们在训练集上训练一个模型，这个模型在训练集上的表现和在新数据下的表现会随着样本数量的增多趋向于一致。
注意这里是趋向一致。就是经验误差大那么泛化也跟着大，经验误差小，泛化误差也跟着小。但我们实际上想要得到是一个泛化误差小的模型。
还有一点注意这是对于某一个假设h，但是其实我们可以推广到任意假设h。

再给出第二条引理：

\[P \left( A _ { 1} \cup \ldots \cup A _ { k } \right) \leq P \left( A _ { 1} \right) + \ldots + P \left( A _ { k } \right) \]

另\(P \left( A _ { i } \right) \leq 2\exp \left( - 2\gamma ^ { 2} m \right)\)
于是我们可以对h进行推广：

\[\left.\begin{aligned} P \left( \exists h \in \mathcal { H } . | \varepsilon \left( h _ { i } \right) - \hat { \varepsilon } \left( h _ { i } \right) | > \gamma \right) & = P \left( A _ { 1} \cup \cdots \cup A _ { k } \right) \\ & \leq \sum _ { i = 1} ^ { k } 2\exp \left( - 2\gamma ^ { 2} m \right) \\ & \leq \sum _ { i = 1} ^ { k } 2\exp \left( - 2\gamma ^ { 2} m \right) \\ & = 2k \exp \left( - 2\gamma ^ { 2} m \right) \end{aligned} \right. \]

注意这里最后多了个k，即假设空间的大小。

如何降低经验误差

通过上面那边的推导我们已经知道了对于特定的h，只要样本数量足够大，那么泛化误差和经验误差趋于一致。而且把这个结论推广到了任意的假设h。但是我们怎么保证模型泛化误差小呢。

首先经验误差最小的假设\(h_i\)肯定是\(\mathcal { H }\)中的一个，所以其实我只要让\(\mathcal { H }\)空间变大，这也就意味着模型更复杂。即可增大找到经验误差最小假设的概率。

到此为止我们的两个问题：

1. 如何保证经验误差和泛化误差趋于一致
2. 如何让经验误差变小

都有了答案。
于是这是不是代表我们只要数据量越大，假设空间越大就一定可以很好的模型呢。
实际上并不是这样的，回顾一下我们推导经验误差和泛化误差一致性的第二条式子：

\[P \left( \exists h \in \mathcal { H } .| \varepsilon \left( h _ { i } \right) - \hat { \varepsilon } \left( h _ { i } \right) | > \gamma \right) \leq 2k \exp \left( - 2\gamma ^ { 2} m \right) \]

当右边不等式中的k也就是假设空间的大小增大的时候，我们经验误差和泛化误差一致性的上界也就会变大，也就是说模型越复杂的话越不能保证经验误差和泛化误差的一致性。即我们不能保证减低经验误差的过程和保证经验误差与泛化误差一致性过程可以同时发生。
这个窘境之后还会提。

模型选择

上一节的内容我们已经说明了在数据量够大，模型复杂度足够的情况下。我们的“学习”是可行的。这一节说一说模型选择的问题。

选择偏好

首先我们的假设函数空间是基本是是无限大的，而我们的数据是有限的，这就导致了一个问题，可能有多个假设符合我们经验误差最小算法的假设。在这样的情况下我们要选择哪个假设呢。

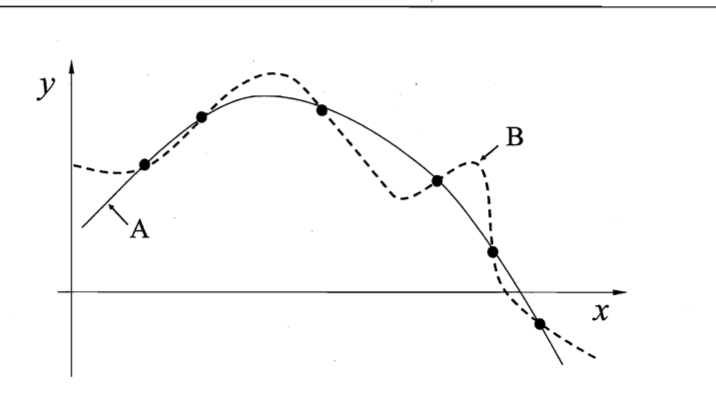
比如这幅图AB曲线都完美的拟合了我们的数据集。所以我们要对选择有一种偏好，要不然学习算法就不知道要选择哪条直线了。那么我们常用的选择偏好就是：奥卡姆剃刀原则，即如果有多个假设与观察一致，则选择最简单那个。其实这个原则在自然科学当中已经有很多应用了。
所以上图的AB两条曲线，我们基于奥卡姆提到的选择偏好，会选择A曲线。但是A曲线就一定会表现得比B好吗。这是不一定的。这就要提到下一个模型选择的定理。

没有免费午餐

那么如上图所示，我们加入了一些测试样本。左图显示测试样本都落在了我们的假设上。但是也有可能是右图那样，我们偏好得到假设完全就是错误的。那个更复杂的曲线才是真实的分布。这都是有可能的。偏好只是偏好，偏好并不代表正确。对于一些问题假设A确实表现得比假设B好。但是完全有可能会出现另外一种假设B比假设A表现好的情况。
甚至这种情况还能再进行推广：如果问题的出现概率和问题的权重都相同，那么任意学习算法的期望性能都是相同的。这个就是没有免费午餐定理。这个推广的详细推导请查看参考。
也就是说，如果所有问题等概率等权重出现，那么再聪明的学习算法也跟瞎猜没什么区别。
那机器学习还有什么意义吗？注意我们强调了，没有免费午餐定理的出现是有前提的。所有问题等概率等权重出现。但是大多数情况下我们只会关注自己正在尝试解决的问题。比如说你在做数学题，你就会用数学题的解法去解数学题。做英语题就用英语题的解法。英语题的解法在数学题和语文题的上解对的概率和瞎猜没什么区别。
没有免费午餐定理主要说明了一件事：脱离具体问题讨论学习算法是没有意义的。

误差分解

再回到泛化误差上面来。西瓜书上还有另一种角度理解泛化误差，我们也可以用简单的多项式展开对期望误差进行分解。
如果这段看不懂也没事，直接看结论就好：
如果\(y_D\)是数据中的标记，\(y\)是真实的标记。\(f(x;D)\)为学习到的模型的预测输出。那么以回归任务为例：
学习算法的期望预测：

\[\overline { f } ( x ) = \mathbb { E } _ { D } [ f ( x ; D ) ] \]

样本数量相同的不同训练集之间的方差：

\[\operatorname{var} ( x ) = \mathbb { E } _ { D } \left[ ( f ( x ; D ) - \overline { f } ( x ) ) ^ { 2} \right] \]

噪声：

\[\varepsilon ^ { 2} = \mathbb { E } _ { D } \left[ \left( y _ { D } - y \right) ^ { 2} \right] \]

期望预测与真实标记之间的差距即偏差：

\[b i a s ^ { 2} ( x ) = ( \overline { f } ( x ) - y ) ^ { 2} \]

假设噪声的期望为零，即\(\mathbb { E } _ { D } \left[ y _ { D } - y \right] = 0\)，那么有：

最终得到了：

\[E ( f ; D ) = \operatorname{bias} ^ { 2} ( x ) + \operatorname{var} ( x ) + \varepsilon ^ { 2} \]

这里包括了一点讲义中没提到的，我们泛化误差其实还有包含一部分，就是采样误差或者称之为噪声。想象一种极端的情况，如果整个数据集的标注完全就是错误的，那么我们得到的假设h根本也就不可能是正确的了。一般来说我们的假定我们的(x,y)来自于真实的数据分布D，但是采样过程其实也会产生误差。

于是我们就可以把泛化误差分解成三个部分，一个方差一个偏差还有一个是噪声。

图像理解

如果我们以一个多项式回归拟合这个点集，即\(y = \theta _ { 0} + \theta _ { 1} x + \cdots \theta _ { 5} x ^ { 5}\)的形式。
一般来说中间这幅图是比较理想的情况。
左边这幅图就是偏差过大的情况，也称之为欠拟合。因为模型太简单，数据再多也救不了，虽然保证了经验误差和泛化误差的一致性，但是经验误差表现得实在是太差了，那么泛化误差也会很大。

右边这幅图就是方差过大的情况，也称之为过拟合。由于模型过于复杂，虽然说每个数据都拟合上了，经验误差很小，但是不能保证泛化误差也很小。

这其实就是我们之前提的，不能保证减低经验误差的过程和保证经验误差与泛化误差一致性过程可以同时发生。
其实用方差和偏差的角度来理解的话，就是偏差和方差不能同时下降。这个我们称之为偏差-方差窘境。

所以就有了偏差-方差权衡(bias-variance tradeoff)，也就是说模型的复杂性其实是一把双刃剑，我们不能让模型太复杂，那样可能会过拟合，也不能让模型太过于简单，那样可能会欠拟合。

正则化

那我们如何做到偏差与方差权衡，让模型的复杂度既能很好拟合样本集但又不会过拟合呢。
以多项式回归为例：
假设函数为：

\[h(x)=\sum_{i=0}^n\theta_i x_i^i \]

即我们不用直线而用曲线拟合。
回忆一下线性回归的损失函数，这里也可以作为多项式回顾的损失函数：

\[\underset{\theta}{\operatorname{argmin}}J(\theta)=\frac12\sum_{i=1}^m(h(x^{(i)}-y^{(i)}))^2 \]

我们这里损失函数就完全是冲着最小化经验误差去的，也就是说如果把这个损失函数下降到最小，我们的方差也下降到了最小。但是可能会容易过拟合，那么。但是我们在损失函数中加入一项来惩罚模型复杂度：

\[\underset{\theta}{\operatorname{argmin}}J(\theta)=\frac12\sum_{i=1}^m(h(x^{(i)}-y^{(i)}))^2+C||\theta||^2 \]

为什么\(||\theta||\)就表示了模型的复杂度了呢。我们可以这样来理解，我们输出预测是由\(\theta^Tx\)得到的。如果θ的值越大那么对x产生预测值的影响也会越大。
于是我们把模型复杂度写进了损失函数，这样再对损失函数进行求解的时候，偏差和方差自己就会达到一个均衡。

k折交叉验证

我们之前都是让模型经验风险最小，那么有没有什么办法能让模型通过取巧的一点办法模拟在真实分布进行泛化误差的测量呢。
这里就提到一种交叉验证的方法。

我们假定我们的数据集是S。

1. 随机把S分为样本数量相同的k个不相交的子集，称为分割集\(S _ { 1} ,\dots ,S _ { k }\)。
2. 从M中选出一个\(M_i\)模型，然后再在分割集中选一个\(S_j\)作为验证集，其他作为训练集。这样在训练集上对i和j按照经验误差最小原则，迭代两轮得到\(h_{i j}\)。
3. 对\(h_{i j}\)在验证集上进行验证得到一个近似的泛化误差$ \hat { \varepsilon } _ { S _ { j } } ( h _ { i j }) $
4. 对于每个\(M_i\)计算起平均的近似泛化误差
5. 选平均近似泛化误差最小对应的那个模型即可

注意这里的泛化误差并不是真正的泛化误差。而是泛化误差的一个近似。

特征选择

问题背景

我们回想一下之前房子分类的问题。如果我们有一个特征集包含单位面积房价、房子面积、房子总价。然后让你处理去处理一个二分类问题。
你会不会感觉哪里有点奇怪。房子总价不就是房子面积*单位面积房价吗。所以房子总价其实就是个多余的特征，对于这样的特征其实我们之间去除。那么再换个角度，我们如何选取我们需要的特征，或者回忆一下我们最终的目的，即我们如何选取特征使我们的模型最终的泛化误差比较小呢。

特征搜索

最简单的想法就是做特征遍历，我们设定一个空的特征集，在这个特征集中不断添加特征，每个添加一次就用这个特征集训练一个模型。然后拿表现最好的模型对应的特征集即可。但是这种方法复杂度有点高，如果你对计算复杂度有所了解的话这里的复杂度应该是O(n^2)。

过滤特征

回忆问题背景中的房子面积其实并没有为我们提供新的信息。再考虑一种极端一点的情况，比如无论这个特征值为多少，对应的y都为一类。那么其实这个特征对于分类就没有任何意义了。
所以我们可以从信息论角度去做特征选取。即对每个特征每个特征\(x_i\)计算对应的标签y的信息量S(i)然后选取前k大信息量的特征即可。
于是问题就是我们要如何衡量信息量了。由于涉及到信息论，我们这里直接给出互信息公式：

\[M I \left( x _ { i } ,y \right) = \sum _ { x _ { i } \in \{ 0,1\} } \sum _ { y \in \{ 0,1\} } p \left( x _ { i } ,y \right) \log \frac { p \left( x _ { i } ,y \right) } { p \left( x _ { i } \right) p ( y ) } \]

这里就先不解释为什么了，有兴趣可以自己了解一下。

参考

1. cs229-note4
2. 采样误差的一些资料可以参考一下《机器学习基石》-林轩田 第八课
3. 以及其他人提供的《机器学习基石》笔记
4. 没有免费午餐定理的推导 《机器学习》-周志华 p9