Spatial Transformer Networks(空间变换神经网络)
Reference:Spatial Transformer Networks [Google.DeepMind]
Reference:[Theano源码,基于Lasagne]
闲扯:大数据不如小数据
这是一份很新的Paper(2015.6),来自于Google旗下的新锐AI公司DeepMind的四位剑桥Phd研究员。
他们针对CNN的特点,构建了一个新的局部网络层,称为空间变换层,如其名,它能将输入图像做任意空间变换。
在我的论文[深度神经网络在面部情感分析系统中的应用与改良]中,提出了一个有趣观点:
大数据不如小数据,如果大数据不能被模型有效利用。
该现象是比较常见的,如ML实战的一个经典问题:数据不均衡,这样模型就会对大类数据过拟合,忽略小类数据。
另外,就是[Evolving Culture vs Local Minima:文化、进化与局部最小值]提到的课程学习观点:
将大数据按照难易度剖分,分批学习,要比直接全部硬塞有效得多。
当前,我们炙手可热的模型仍然是蒟蒻的,而数据却是巧夺天工、超乎想象的。
因而,想要通过模型完全摸清数据的Distribution是不现实的,发明、改良模型结构仍然是第一要务,
而不单纯像Li Feifei教授剑走偏锋,用ImageNet这样的大数据推进深度学习进程。
空间变换的重要意义
在我的论文[深度神经网络在面部情感分析系统中的应用与改良]中,分析了CNN的三个强大原因:
[局部性]、[平移不变性]、[缩小不变性],还对缺失的[旋转不变性]做了相应的实验。
这些不变性的本质就是图像处理的经典手段,[裁剪]、[平移]、[缩放]、[旋转]。
这些手段又属于一个家族:空间变换,又服从于同一方法:坐标矩阵的仿射变换。
那么,神经网络是否有办法,用一种统一的结构,自适应实现这些变换呢?DeepMind用一种简易的方式实现了。
图像处理技巧:仿射矩阵、逆向坐标映射、双线性插值
1.1 仿射变换矩阵
实现[裁剪]、[平移]、[缩放]、[旋转],只需要一个$[2,3]$的变换矩阵:
$\begin{bmatrix}\theta_{11} & \theta_{12} & \theta_{13} \\ \theta_{21}& \theta_{22} & \theta_{23}\end{bmatrix}$
—————————————————————————————————————————————————————————
对于平移操作,坐标仿射矩阵为:
$\begin{bmatrix}1 & 0 & \theta_{13} \\ 0& 1 & \theta_{23}\end{bmatrix}\begin{bmatrix}x\\ y\\1\end{bmatrix}=\begin{bmatrix}x+\theta_{13}\\
y+\theta_{23}\end{bmatrix}$
—————————————————————————————————————————————————————————
对于缩放操作,坐标仿射矩阵为:
$\begin{bmatrix}\theta_{11} & 0 & 0 \\ 0& \theta_{22} & 0\end{bmatrix}\begin{bmatrix}x\\ y\\1\end{bmatrix}=\begin{bmatrix}\theta_{11}x\\
\theta_{22}y\end{bmatrix}$
—————————————————————————————————————————————————————————
对于旋转操作,设绕原点顺时针旋转$\alpha$度,坐标仿射矩阵为:
$\begin{bmatrix}cos(\alpha) & sin(\alpha) & 0 \\ -sin(\alpha)& cos(\alpha) & 0\end{bmatrix}\begin{bmatrix}x\\ y\\1\end{bmatrix}=\begin{bmatrix}
cos(\alpha)x+sin(\alpha)y\\ -sin(\alpha)x+cos(\alpha)y\end{bmatrix}$
这里有个trick,由于图像的坐标不是中心坐标系,所以只要做下Normalization,把坐标调整到[-1,1]。
这样,就绕图像中心旋转了,下文中会使用这个trick。
—————————————————————————————————————————————————————————
至于裁剪操作,没有看懂Paper的关于左2x2 sub-matrix的行列式值的解释,但可以从坐标范围解释:
只要$x^{'}$、$y^{'}$的范围比$x$,$y$小,那么就可以认为是目标图定位到了源图的局部。
这种这种仿射变换没有具体的数学形式,但肯定是可以在神经网络搜索过程中使用的。
1.2 逆向坐标映射
注:感谢网友@载重车提出疑问,修正了这部分的内容。具体请移步评论区。
★本部分作为一个对论文的错误理解,保留。
在线性代数计算中,一个经典的求解思路是:
$\begin{bmatrix}\theta_{11} & \theta_{12} & \theta_{13} \\ \theta_{21}& \theta_{22} & \theta_{23}\end{bmatrix}\begin{bmatrix}x^{Source}\\ y^{Source}\\ 1\end{bmatrix}=\begin{bmatrix}x^{Target}\\ y^{Target}\end{bmatrix}$
这种做法在做图像处理时,会给并行矩阵程序设计造成尴尬——需要牺牲额外的空间存储映射源,:
由于$(x^{Target},y^{Target})$必然是离散的,当我们需要得到$Pixel(x^{Target},y^{Target})$的值时,
如果不及时保存$(x^{Source},y^{Source})$,那么就必须即时单点复制$Pixel(x^{Source},y^{Source})->Pixel(x^{Target},y^{Target})$
显然,这种方法的实现依赖于$For$循环:
$For(0....i....Height)\\ \quad For(0....j....Width) \\ \quad \quad Calculate\&Copy$
为了能让矩阵并行计算成为可能,我们需要逆转一下思路:
$\begin{bmatrix}\theta_{11} & \theta_{12} & \theta_{13} \\ \theta_{21}& \theta_{22} & \theta_{23}\end{bmatrix}^{'}\begin{bmatrix}x^{Target}\\ y^{Target}\\ 1\end{bmatrix}=\begin{bmatrix}x^{Source}\\ y^{Source}\end{bmatrix}$
之后,构建变换目标图就转化成了,数组下标取元素问题:
$PixelMatrix^{Target}=PixelMatrix^{Source}[x^{Source},y^{Source}]$
这依赖于仿射矩阵的一个性质:
$\begin{bmatrix}\theta_{11} & \theta_{12} & \theta_{13} \\ \theta_{21}& \theta_{22} & \theta_{23}\end{bmatrix}^{'}=\begin{bmatrix}\theta_{11} & \theta_{12} & \theta_{13} \\ \theta_{21}& \theta_{22} & \theta_{23}\end{bmatrix}^{-1}$
即,由Target变换为Source时,新仿射矩阵为源仿射矩阵的逆矩阵。
1.3 双线性插值
考虑一个$[1,10]$图像放大10倍问题,我们需要将10个像素,扩展到为100的数轴上,整个图像应该有100个像素。
但其中90个对应Source图的坐标是非整数的,是不存在的,如果我们用黑色($RGB(0,0,0)$)填充,此时图像是惨不忍睹的。
所以需要对缺漏的像素进行插值,利用图像数据的局部性近似原理,取邻近像素做平均生成。
双线性插值是一个兼有质量与速度的方法(某些电子游戏里通常这么排列:线性插值、双线性插值....):

如果$(x^{Source},y^{Source})$是实数坐标,那么先取整(截尾),然后沿轴扩展$d$个坐标单位,得到$P_{21}$、$P_{12}$、$P_{22}$
一般的(源码中),取$d=1$,式中分母全被消去,再利用图中双线性插值式进行插值,得到$Pixel(x^{Source},y^{Source})$的近似值。
神经网络
2.1 块状神经元
CNN是一个变革的先驱者模型,它率先提出局部连接观点,减少网络广度,增加网络深度。
局部连接让神经元呈块状,单参数成参数组;让网络2D化,切合2D图像;让权值共享,大幅度减少参数量。
仿射矩阵自适应学习理论,因此而得以实现:
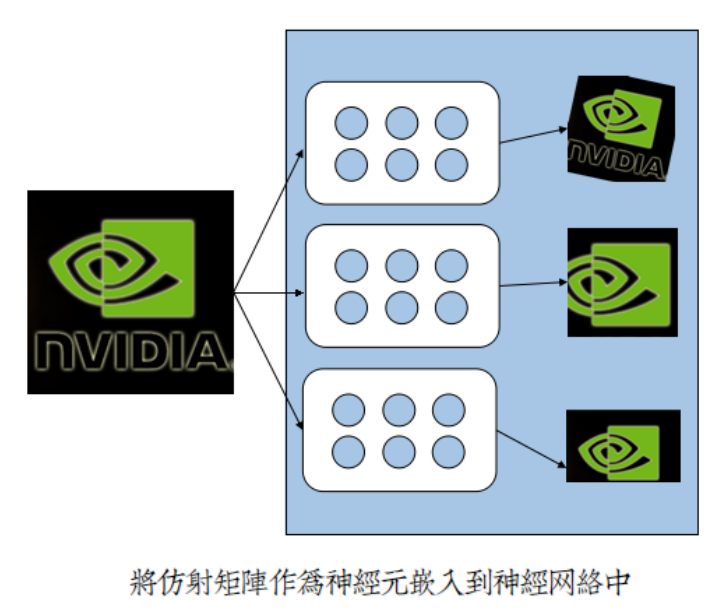
2.2 基本结构与前向传播
论文中的结构图描述得不是很清楚,个人做了部分调整,如下:
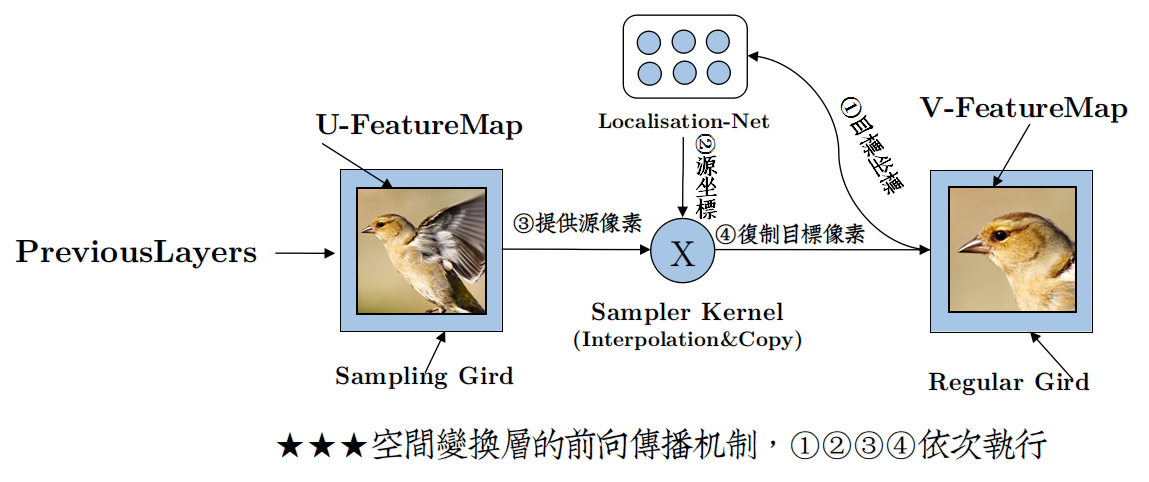
DeepMind为了描述这个空间变换层,首先添加了坐标网格计算的概念,即:
对应输入源特征图像素的坐标网格——Sampling Grid,保存着$(x^{Source},y^{Source})$
对应输出源特征图像素的坐标网格——Regluar Grid ,保存着$(x^{Target},y^{Target})$
然后,将仿射矩阵神经元组命名为定位网络 (Localisation Network)。
对于一次神经元提供参数,坐标变换计算,记为 $\tau_{\theta}(G)$,根据1.2,有:
$\tau_{\theta}(G_{i})=\begin{bmatrix}\theta_{11} & \theta_{12} & \theta_{13} \\ \theta_{21}& \theta_{22} & \theta_{23}\end{bmatrix}^{'}\cdot\begin{bmatrix}x_{i}^{Target}\\ y_{i}^{Target}\\ 1\end{bmatrix}=\begin{bmatrix}x_{i}^{Source}\\ y_{i}^{Source}\end{bmatrix}\quad where \quad i=1,2,3,4..,H*W$
该部分对应于图中的①②,但是与论文中的图有些变化,可能是作者并没有将逆向计算的Trick搬到结构图中来。
所以你看到的仍然是Sampling Grid提供坐标给定位网络,而具体实现的时候恰好是相反的,坐标由Regluar Grid提供。
————————————————————————————————————————————————————————
Regluar Grid提供的坐标组是顺序逐行扫描坐标的序列,序列长度为 $[Heght*Width]$,即:
将2D坐标组全部1D化,根据在序列中的位置即可立即算出,在Regluar Grid中位置。
这么做的最大好处在于,无须额外存储Regluar Grid坐标$(x^{Target},y^{Target})$。
因为从输入特征图$U$数组中,按下标取出的新像素值序列,仍然是逐行扫描顺序,简单分隔一下,便得到了输出特征图$V$。
该部分对应于图中的③。
————————————————————————————————————————————————————————
(1.3)中提到了,直接简单按照$(x^{Source},y^{Source})$,从源像素数组中复制像素值是不可行的。
因为仿射变换后的$(x^{Source},y^{Source})$可以为实数,但是像素位置坐标必须是整数。
为了解决像素值缺失问题,必须进行插值。插值核函数很多,源码中选择了论文中提供的第二种插值方式——双线性插值。
(1.3)的插值式非常不优雅,DeepMind在论文利用max与abs函数,改写成一个简洁、优雅的插值等式:
$V_{i}^{c}=\sum _{n}^{H}\sum _{m}^{W}U_{nm}^{c}\max(0,1-|x_{i}^{S}-m|)\max(0,1-|y_{i}^{S}-n|) \quad where \quad i\in [1,H^{'}W^{'}],c\in[1,3]$
两个 $\sum$ 实际上只筛出了四个邻近插值点,虽然写法简洁,但白循环很多,所以源码中选择了直接算4个点,而不是用循环筛。
该部分对应图中的④。
2.3 梯度流动与反向传播
添加空间变换层之后,梯度流动变得有趣了,如图:
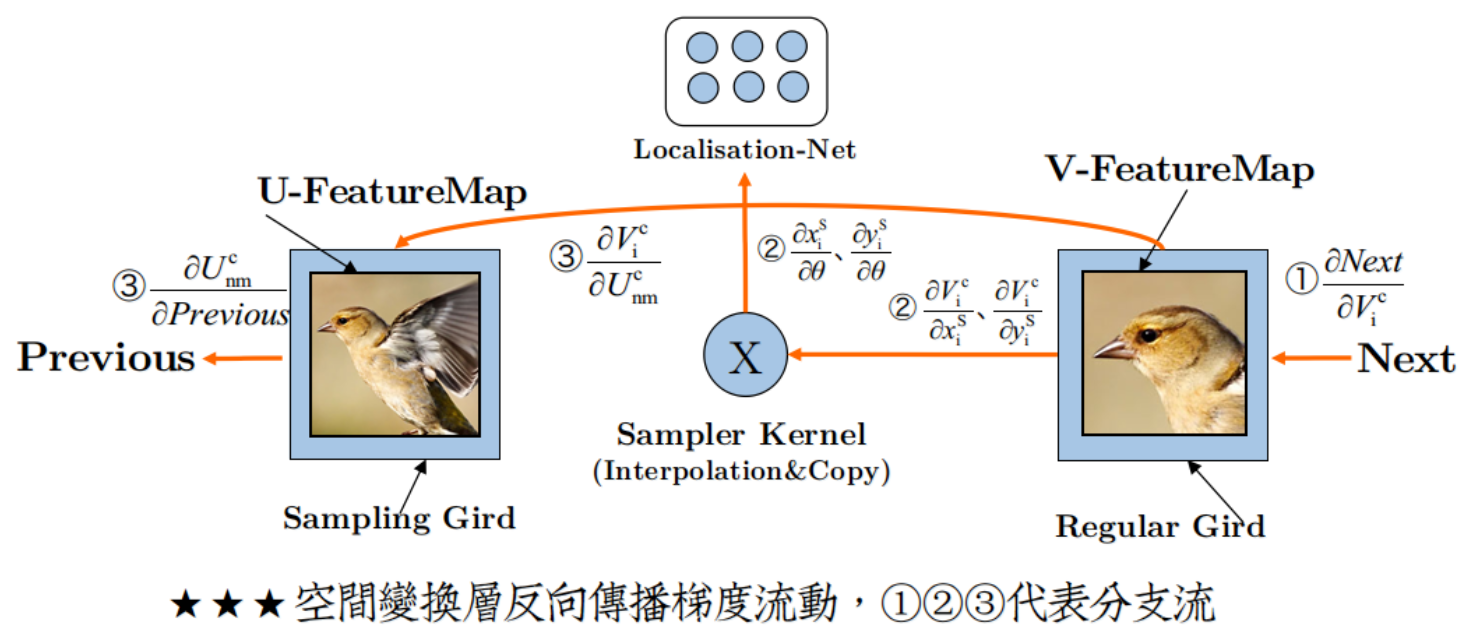
形成了三股分支流:
(I)后の流:
$ErrorGradient\rightarrow .....\rightarrow \frac{\partial Next}{\partial V_{i}^{c}}$
这是Back Propagation从后层继承的动力源泉,没有它,你就不可能完成Back Propagation。
(II)里の流:
$\left\{\begin{matrix}\frac{\partial V_{i}^{c}}{\partial x_{i}^{S}}\rightarrow \frac{\partial x_{i}^{S}}{\partial \theta}\\ \frac{\partial V_{i}^{c}}{\partial y_{i}^{S}}\rightarrow \frac{\partial y_{i}^{S}}{\partial \theta}\end{matrix}\right.$
个人对这股流的最好描述就是:一江春水流进了小黑屋。
是的,你没有看错,这股流根本就没有流到网络开头,而是在定位网络处就断流了。
由此来看,定位网络就好像是在主网络旁侧偷建的小黑屋,是一个违章建筑。
所以也无怪乎作者说,定位网络直接变成了一个回归模型,因为更新完参数,流就断了,独立于主网络。
(III)前の流:
$\frac{\partial V_{i}^{c}}{\partial U_{nm}^{i}}\rightarrow\frac{\partial U_{nm}^{i}}{\partial Previous}$
这是Back Propagation传宗接代的根本保障,没有它,Back Propagation就断子绝孙了。
2.4* 局部梯度
论文中多次出现[局部梯度](Sub-Gradient) 的概念。
作者们反复强调,他们写的,优雅简洁的采样核函数,是不连续的,不能如下直接求导:
$g=\frac{\partial V_{i}^{c}}{\partial \theta}$
而应该是分两步,先对$x_{i}^{S}$ 、$x_{i}^{S}$ 求局部梯度: $\frac{\partial V_{i}^{c}}{\partial x_{i}^{c}}$ 、$\frac{\partial V_{i}^{c}}{\partial y_{i}^{c}}$,后有:
$\left\{\begin{matrix}g=\frac{\partial V_{i}^{c}}{\partial x_{i}^{S}} \cdot \frac{\partial x_{i}^{S}}{\partial \theta}\\ g=\frac{\partial V_{i}^{c}}{\partial y_{i}^{S}} \cdot \frac{\partial y_{i}^{S}}{\partial \theta}\end{matrix}\right.$
有趣的是,对于Theano这种自动求导的Tools,局部梯度可以直接被忽视。
因为Theano的Tensor机制,会聪明地讨论并且解离非连续函数,追踪每一个可导子式,即便你用了作者们的优雅的采样函数,
Tensor.grad函数也能精确只对筛出的4个点求导,所以在Theano里讨论非连续函数和局部梯度,是会被贻笑大方的。


