Long-Short Memory Network(LSTM长短期记忆网络)
自剪枝神经网络
Simple RNN从理论上来看,具有全局记忆能力,因为T时刻,递归隐层一定记录着时序为1的状态
但由于Gradient Vanish问题,T时刻向前反向传播的Gradient在T-10时刻可能就衰减为0。
从Long-Term退化至Short-Term。
尽管ReLU能够在前馈网络中有效缓解Gradient Vanish,但RNN的深度过深,替换激活函数治标不治本。
$\left | \prod_{j=p+1}^{t}\frac{\partial b_{h}^{j}}{\partial b_{h}^{j-1}}\right |\leqslant (\beta_{W}\cdot\beta_{h})^{t-p} \quad where \quad \beta =UpperBound$
上式中指明的根源所在,由于W和h两个矩阵多次幂导致受数值影响敏感,简而言之就是深度过大。
大部分Long-Term情况下,不需要提供路径上完整的信息,但反向传播还是循规蹈矩地穿过这些冗深度。

解决方案之一是,设置可自主学习的参数来屏蔽掉这些无用的信息,与"降维"相似,这种方法叫"降层"

神经网络的剪枝策略很简单,就是添加参数矩阵,经过一定周期的学习,选择性屏蔽掉输入,精简网络。
从结构上来看,类似“树套树”,就是”神经网络套神经网络“。
动态门结构
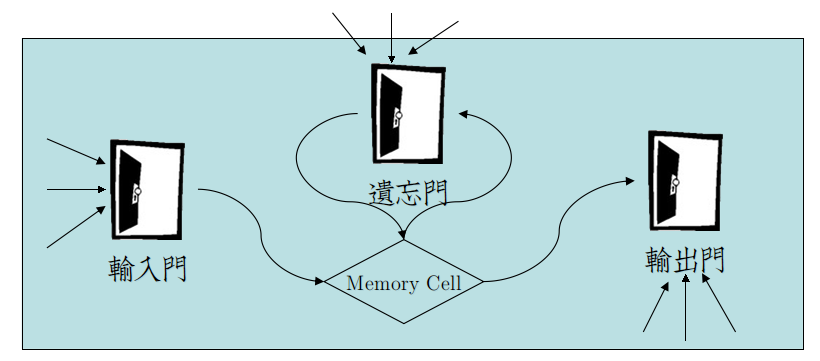
简单概括:
★LSTM将RNN的输入层、隐层移入Memory Cell加以保护
★Input Gate、Forget Gate、Output Gate,通过训练参数,将Gate或开(置1)或闭(置0),保护Cell。
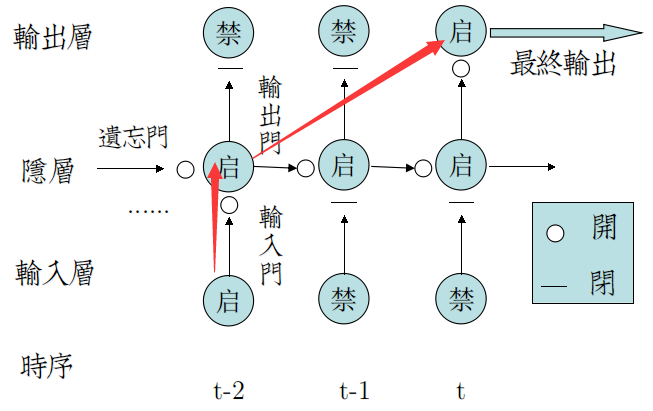
在时序展开图上则更加清晰:
公式定义
原版LSTM最早在[Hochreiter&Schmidhuber 97]提出。
今天看到的LSTM是[Gers 2002]改良过的 extended LSTM。
extended LSTM扩展内容:
★Forget Gate,用于屏蔽t-1以及之前时序信息。
在时序展开图上,由左侧锁住以保护Cell。
★三态门控:
97年提出的Gate输入类似RNN,分为两态Weight矩阵:
☻Wx——序列输入信息
☻Wh——递归隐态输入信息
2002年补充了第三态:
☻Wc——递归Cell态输入信息
将Cell的时序状态引入Gate,称为Peephole Weights。
唯一作用似乎是提升LSTM精度,Alex Graves的博士论文中这么说:
The peephole connections,meanwhile, improved the LSTM’s ability to learn tasks that require precise
timing and counting of the internal states.
具体实现的时候,为了增加计算效率,可以忽视:
Theano的Tutorial中这么说道:
The model we used in this tutorial is a variation of the standard LSTM model.
In this variant, the activation of a cell’s output gate does not depend on the memory cell’s state  .
.
This allows us to perform part of the computation more efficiently (see the implementation note, below, for details).
而CS224D Lecture8中压根就没提。
所以双态Gate可能是更为主流的LSTM变种。
2.1 前向传播
输入门:
$i_{t}=Sigmoid(W_{i}x_{t}+U_{i}h_{t-1}+V_{i}C_{t-1})$ ①
遗忘门:
$f_{t}=Sigmoid(W_{f}x_{t}+U_{f}h_{t-1}+V_{f}C_{t-1})$ ②
输出门:
$O_{t}=Sigmoid(W_{o}x_{t}+U_{o}h_{t-1}+V_{o}C_{t})$ ③
原始Cell(RNN部分):
$\tilde{C_{t}}=Tanh(W_{c}x_{t}+U_{c}h_{t-1})$ ④
门套Cell:
$C_{t}=i_{t}\cdot\tilde{C_{t}}+f_{t}\cdot C_{t-1}$ (输入门+遗忘门) ⑤
$h_{t}=O_{t}\cdot Tanh(C_{t}) \quad where \quad h_{t}=FinalOutput$ (输出门) ⑥
————————————————————————————————————————————————————
仔细观察①②③④,发现除了Peephole Weights引入的$V$阵,这四个式子是一样的。
Theano中为了GPU能够一步并行计算,没有使用Peephole Weights,这样①②③④就是一个基本并行模型:
以相同的代码,运算数据集在空间中的不同部分。


