【初识——最大流】 hdu 1532 Drainage Ditches(最大流) USACO 93
最大流首次体验感受——
什么是最大流呢?
从一个出发点(源点),走到一个目标点(汇点),途中可以经过若干条路,每条路有一个权值,表示这条路可以通过的最大流量。
最大流就是从源点到汇点,可以通过的最大流量。
接下来我们看一个图——
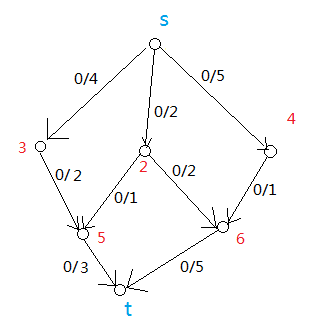 图1
图1
这个图中,s是源点,t是汇点。期间可以经过2, 3, 4, 5, 6几个点。每条边上有两个权值,其中第一个表示当前通过这条边的流量,第二个表示这条边最大可以通过的流量。
最佳情况,即最大可以通过的流量的一种情况是这样的——
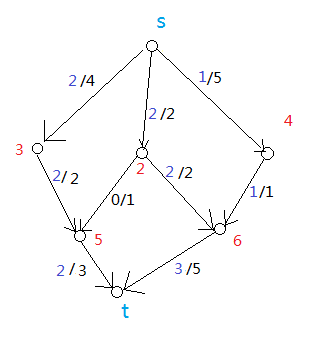 图2
图2
但还有一种情况,同样可以达到最大流——
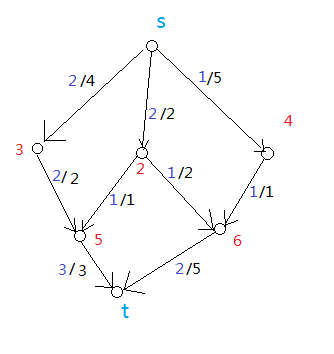 图3
图3
这里得到两个结论:
1. 每条路径中都有至少一条边是满的。
2. 最大流可能不止一种情况。
接下来我们再看另一个图:
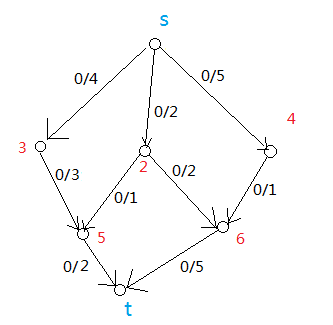 图4
图4
如果在这个图上找最大流该怎么找?
这样?
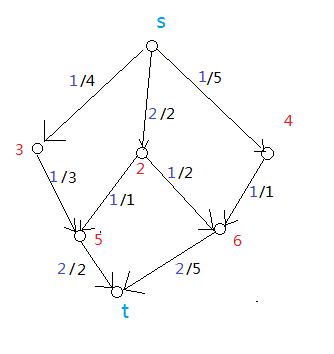 图5
图5
不对,这个图乍一看好像满足每条路径上都有一个满流的边这个条件,但是其实还有更大的流——
 图6
图6
怎么办呢?
我们可以通过这个方式从图5变到图6——
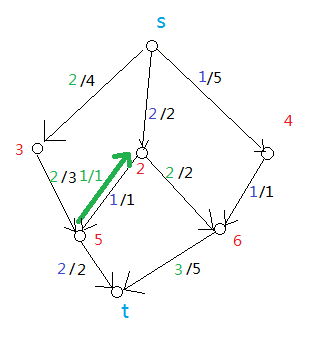 图7
图7
这里我们的可以这样理解,在我们走出图5 的结果以后,我们允许图中出现图7中的绿色的边,然后我们就得到了绿色的数字所标示出的一条新路,通过这条路径,我们就获得了最大流。
如果我们获得了一个流量图,这个流量图中每条路径上都有一条边是满流了,如何判断这是不是一个最大流的图呢?通过上面的方法,我们在通过某条边之后,在这两个点之间构造一条反向的并且和通过的流量大小相同的边(称为反向边)。这样,就可能产生一条新路,使整个图中的流量增加。那么,我们不断地构造这种边,直到无法寻找到新的路径为止(称为增广路径),是不是就得到了最大流呢?
总结起来,每次找到一条增广路,增广路中每条边的值,都减去路径中,边值最小的边的值(读起来很凹口是不是?多读几遍就好了)。同时,还要给每条边都加上反向边。重复寻找,直到找不到新的路径,我们就获得了这个图的最大流。
注意,
- 每次寻找增广路径后,我们都会将原图更改,这样,我们会得到一个新的图。
- 在获得最大流的图之前,我们获得的每张图都称为残余网络。原始图也可以视为残余网络。
以上讲的是寻找最大流的思想。
但是,寻找增广路径的方法不止一种。
我最直接想到的方法,使用dfs多次搜索这张图,直到找不到为止。

1 #include <cstdio> 2 #include <cmath> 3 #include <cstring> 4 #include <algorithm> 5 using namespace std; 6 7 const int N = 210; 8 const int M = 10000010; 9 10 int n, m; 11 int mp[N][N]; //保存地图信息,有向图 12 bool vis[N][N]; //dfs时标记使用 13 int ans; //最终结果 14 15 void init() 16 { 17 memset(mp, 0, sizeof(mp)); 18 memset(vis, 0, sizeof(vis)); 19 for(int i = 0; i < n; i++) 20 { 21 int a, b, c; 22 scanf("%d%d%d", &a, &b, &c); 23 mp[a][b] += c; 24 } 25 ans = 0; 26 } 27 28 int dfs(int x, int maxn) 29 { 30 if(x == m) 31 { 32 ans += maxn; //每次走到汇点后增加的流量 33 return maxn; 34 } 35 int flow = 0; 36 for(int i = 1; i <= m; i++) 37 { 38 if(mp[x][i] > 0 && !vis[x][i]) 39 { 40 vis[x][i] = 1; 41 int mmaxn = maxn < mp[x][i] ? maxn : mp[x][i]; //取本路径中所可以通过的最小值 42 int mid; 43 if(mmaxn > 0) mid = dfs(i, mmaxn); //如果此路仍然是通路,则继续搜索 44 if(mid > 0) 45 { 46 mp[x][i] -= mid; //已经经过的路要减去耗费的流量 47 mp[i][x] += mid; //反向路(弧)增加耗费的流量 48 maxn -= mid; //走过一条通路后剩余的流量 49 flow += mid; //已经消耗的流量 50 if(maxn == 0) break; 51 } 52 } 53 } 54 return flow; 55 } 56 57 int main() 58 { 59 //freopen("test.in", "r", stdin); 60 while(~scanf("%d%d", &n, &m)) 61 { 62 init(); 63 while(dfs(1, M) > 0) memset(vis, 0, sizeof(vis)); 64 printf("%d\n", ans); 65 } 66 return 0; 67 }
但是后来我突然想到。dfs找到的不一定最短路,每次搜索可能会浪费时间,然后又改成了bfs,这种方法也就是常说的Edmonds-Karp算法。

1 #include <cstdio> 2 #include <cmath> 3 #include <cstring> 4 #include <algorithm> 5 #include <queue> 6 using namespace std; 7 8 const int N = 210; 9 const int M = 100000010; 10 11 int mp[N][N]; 12 int fm[N]; //用于记录路径 13 int val[N]; 14 int n, m; 15 int ans; 16 17 void init() 18 { 19 memset(mp, 0, sizeof(mp)); 20 for(int i = 0; i < n; i++) 21 { 22 int a, b, c; 23 scanf("%d%d%d", &a, &b, &c); 24 mp[a][b] += c; 25 } 26 ans = 0; 27 } 28 29 void work() 30 { 31 while(1) 32 { 33 memset(val, 0, sizeof(val)); 34 val[1] = M; 35 queue<int> que; 36 que.push(1); 37 while(!que.empty()) //spfa,寻找最短路 38 { 39 int k = que.front(); 40 que.pop(); 41 if(k == m) break; 42 for(int i = 1; i <= m; i++) 43 { 44 if(!val[i] && mp[k][i] > 0) 45 { 46 fm[i] = k; 47 que.push(i); 48 val[i] = val[k] < mp[k][i] ? val[k] : mp[k][i]; 49 } 50 } 51 } 52 if(val[m] == 0) break; //当前图上找不到源点到汇点的通路,则退出 53 54 for(int i = m; i != 1; i = fm[i]) 55 { 56 mp[fm[i]][i] -= val[m]; //经过的路径上要减去耗费的流量 57 mp[i][fm[i]] += val[m]; //反向路径(弧)增加相应的路径 58 } 59 //printf("%5d\n", val[m]); 60 ans += val[m]; //结果增加新增的流量 61 } 62 } 63 64 void outit() 65 { 66 printf("%d\n", ans); 67 } 68 69 int main() 70 { 71 while(~scanf("%d%d", &n, &m)) 72 { 73 init(); 74 work(); 75 outit(); 76 } 77 return 0; 78 }
接下来又找到了一种看起来很高大上的方法——Dinic算法。
这个方法要说一说,因为我也花了不少时间来理解,虽然还没有完全理解,但是已经被它所包含的思想震撼了。
这个算法是一层一层搜索的。简单来说,就是:
1)将这个图中用bfs遍历一遍,严格确立每个点的层次。
如果使用bfs可以从源点走到汇点,那么执行2),否则这张图中不存在新的增广路,算法结束。
2)从源点开始dfs,寻找到当前图中所有从源点到汇点的路径,在寻找时,严格按照点的层次寻找,只能从第i层的点走到第i+1层的点。
3)重复1)。
好神奇的方法。

1 #include <cstdio> 2 #include <cmath> 3 #include <cstring> 4 #include <algorithm> 5 #include <queue> 6 using namespace std; 7 8 const int N = 210; 9 const int M = 100000010; 10 11 int mp[N][N]; 12 int dis[N]; 13 int cur[N]; 14 bool vis[N]; 15 int n, m; 16 int ans; 17 18 void init() 19 { 20 memset(mp, 0, sizeof(mp)); 21 for(int i = 0; i < n; i++) 22 { 23 int a, b, c; 24 scanf("%d%d%d", &a, &b, &c); 25 mp[a][b] += c; 26 } 27 ans = 0; 28 } 29 30 bool bfs() 31 { 32 memset(vis, 0, sizeof(vis)); 33 queue<int> que; 34 que.push(1); 35 dis[1] = 0; 36 vis[1] = 1; 37 while(!que.empty()) 38 { 39 int k = que.front(); 40 que.pop(); 41 for(int i = 1; i <= m; i++) 42 { 43 if(!vis[i] && mp[k][i] > 0) 44 { 45 vis[i] = 1; 46 dis[i] = dis[k]+1; 47 que.push(i); 48 } 49 } 50 } 51 return vis[m]; 52 } 53 54 int dfs(int x, int val) 55 { 56 if(x == m) return val; 57 int flow = 0, minn; 58 for(int& i = cur[x]; i <= m; i++) //随着i的变化改变cur[x],这样可以节省当前图中下次使用x时耗费的时间 59 { 60 int mval = val < mp[x][i] ? val : mp[x][i]; //记录当前路径中的最小的边的权,最后要根据它建立反向边 61 if(dis[x]+1 == dis[i]) 62 { 63 minn = 0; 64 if(mval > 0) minn = dfs(i, mval); 65 if(minn > 0) 66 { 67 mp[x][i] -= minn; 68 mp[i][x] += minn; 69 flow += minn; 70 val -= minn; 71 if(val == 0) break; 72 } 73 } 74 75 } 76 return flow; 77 } 78 79 void work() 80 { 81 while(bfs()) //如果存在增广路,则dfs寻找,否则结束 82 { 83 for(int i = 1; i <= m; i++) cur[i] = 1; 84 ans += dfs(1, M); 85 } 86 } 87 88 void outit() 89 { 90 printf("%d\n", ans); 91 } 92 93 int main() 94 { 95 //freopen("test.in", "r", stdin); 96 while(~scanf("%d%d", &n, &m)) 97 { 98 init(); 99 work(); 100 outit(); 101 } 102 return 0; 103 }




