作者:高焕堂,misoo.tw@qq.com
首页:Back
介绍溯因推理、减法设计与未来性
★ 溯因推理是去猜测现象的可能原因,具有高度灵活性,是具创造性、未来性的推理方法
★ 溯因逻辑是<假定-否证>的逻辑,透过检验方式,发现走不通的路,就删除之(减法)
★ 熟悉溯因思考,就能拥有诸葛亮(孔明)的高度创意(如三分天下和空城计)
★ 将 {溯因, 减法,创造} 组合运用,就像麦肯锡公司一样,展现高度的商业价值
1. 基本观念
溯因推理是由观察现象(结果)到原因的猜测推导过程,沿着现象的特征往回追溯产生该现象之原因;它是除了演绎推理、归纳推理之外的第三种逻辑推理方法。运用这种方法去猜测现象的可能原因,受逻辑规则制约的程度较小,具有高度的灵活性,是一种颇具创造性的推理方法。
演绎推理
推理R:停在斑马线上的车子都会被开罚单
P:这些车子停在斑马线
Q:这些车子都会被开罚单
归纳推理
P:这些车子都停在斑马线上
Q:这些车子都被开了罚单
(可能性)推理R:停在斑马线上的车子都会被开罚单
溯因推理
Q:这些车子都被开了罚单
(假定性)推理H:停在斑马线上的车子都会被开罚单
(可能性)P:这些车子都停在斑马线上
在这个溯因推理方法中,假定性推理(Hypothesis)的内容就是:若P(车子停在斑马线上),则Q(车子会被开罚单)。一般而言,要去正面性实证这项假定性推理,可能大费周章;然而,却能轻易地从反面去”否证”它。
刚才说过,这个假定性推理的内容就是:<若P则Q>。当这个<若P则Q>是真时,就表示<若~Q则~P>的推理也是真。基于Q是已知的事实,我们可以观察~Q的现象,然后从中寻觅其中之一是P原因所产生的结果。只要找到其中之一,就足以否证了这项假定性推理。这也就是俗称的”假定-否证”思维方法。例如,停在斑马线上的车子,发现了其中一辆或多辆车子没被罚,就否定掉该项假定性推理了。
2. 孔明的溯因推理范例
为了更通俗易懂起见,刚才的溯因推理范例,可以简化如下:
溯因推理
(假定性)推理H:车子停在斑马线上都会被开罚单
否证:停在斑马线上的车子,发现了其中一辆或多辆车子没被罚
这可以更简单地表现出”假定-否证”的思维。例如,请你观摩一下诸葛亮的溯因推理范例:
孔明的溯因推理(範例版本一)
目标:刘备想当皇帝
(假定性)推理H_1:直接北伐曹操(一分天下)是可行的手段
否证:”今操已拥百万之众,挟天子而令诸侯,此诚不可与争锋”(<<隆中对>>原文)
(假定性)推理H_2:先取孙权(二分天下)是可行的手段
否证:”孙权据有江东,已历三世,国险而民附,贤能为之用,此可以为援而不可图也”(<<隆中对>>原文)
(假定性)推理H_3:先取益州刘璋(三分天下)是可行的手段
否证:(没有足以否定的证据)
上述的叙述(版本一),并没有凸显出<目的-手段>的关系,于是将其更改为新版本,如下:
孔明的溯因推理(範例版本二)
目标(Goal):刘备想当皇帝
手段(How-to)_1:采 ”一分天下” 策略(直接北伐曹操)
假定(Hypothesis)_1:有能力打败曹操
否证:”今操已拥百万之众,挟天子而令诸侯,此诚不可与争锋”(<<隆中对>>原文)
手段(How-to)_2:采先 ”二分天下” 策略(先攻打孙权)
假定(Hypothesis)_2:有能力打败孙权
否证:”孙权据有江东,已历三世,国险而民附,贤能为之用,此可以为援而不可图也”(<<隆中对>>原文)
手段(How-to)_3:采先 ”三分天下” 策略(先进益州)
假定(Hypothesis)_3:有能力进益州
否证:(没有足以否定的证据)
这能明显地看出来,有三种可能的手段来实现刘备的目标。但起背后都有一个假设(Assumption)或称假定(Hypothesis):有能力执行该手段。如果能找到证据去否定该项假设或假定,就等于否定了该项手段。
3. 溯因推理与敏捷(软件)开发
首先,以图来表达溯因推理与演绎(或归纳)推理的不同,如下:

图-1. 溯因推理与演绎(或归纳)推理的不同
因逻辑(右图)是<假定-否证>的逻辑,而不是”实证”逻辑,这是大家最常误解的地方。在传统的Waterfall软件开发里,属于演绎逻辑(左图):从需求可演绎出来代码和架构。现在的敏捷开发,属于朔因逻辑(右图):架构和代码都不是纯然从需求演绎出来,而是假定-否证的逻辑。所以,敏捷的TDD主要任务不是来证实你的架构和代码,而是来否证,并将被否定的部分反馈回去给架构师和开发者,而带动一次新的迭代。典型的敏捷软件开发,其图示如下:

图-2. 此敏捷开发幕后也是溯因推理
从图1和图2里,你可以看出来,敏捷开发的幕后也是溯因推理。
4. 麦肯锡(McKinsey)公司的减法设计
– 基于MECE原则来拟定扎实的议题起始假定(Initial Hypothesis)
– 然后展开探索更细节的议题假定,逐渐建立出扎实而完整的树状议题架构(又称议题树)
– 议题树包含一系列有待检验(否证)其假定(Hypothesis)的议题
– 依循溯因的<假定-否证>逻辑,透过检验方式,发现走不通的路,就指示不必去探索该议题了
4.1 问题架构(Problem Architecture)设计:建立假定性的议题(Issue)树
MECE原则
溯因逻辑是<假定-否证>的逻辑,而不是”实证”逻辑。那么,如何拟定扎实的假定(Competent Hypothesis),做为问题探讨的理想起点,并指引出后续探索之路呢? 这有许多模式可以依循,其中最著名的是麦肯锡公司提出的 (mutually exclusive, collectively exhaustive)模式:
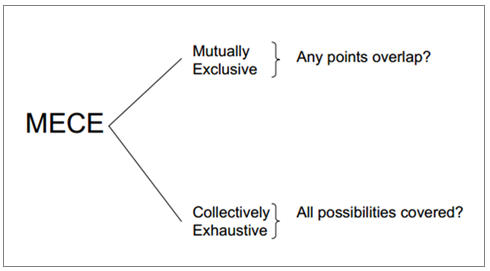
图-3. 麦肯锡公司提出的MECE
议题树及其种类原
基于MECE则来拟定扎实的议题起始假定(Initial Hypothesis);然后展开探索更细节的议题假定,逐渐建立出扎实而完整的树状议题架构(又称议题树)。议题树包含一系列有待检验(否证)其假定(Hypothesis)的议题。如下图:
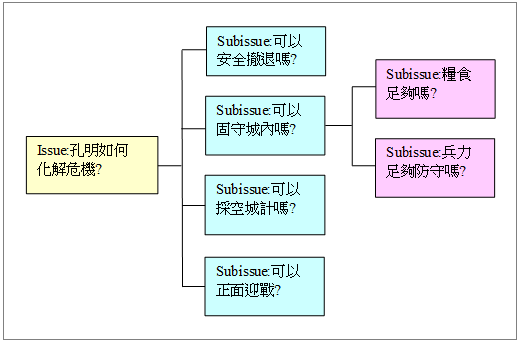
图-4. 麦肯锡的树状议题架构(又称议题树)
建立一个合乎MECE条件的逻辑树,已经证明是极为有效的问题解决方法,可掌握问题的整体架构,有脉络地思考问题的核心。藉由「因-果」之逻辑关系,或是「目的-手段」之逻辑关系而把重要的议题(Issue)连结起来,形成一个树状结构,称为议题树。例如上述的「孔明如何化解危机?」议题树就是一种<目的-手段>关系之议题树。
除了<因-果>议题树和<目的-手段>议题树之外,还有一种常见的议题树就是:<结论-理由>议题树。它经常呈现出金字塔形状,所以又称为金字塔结构(Pyramid Structure)。此议题树连结了结论与理由之间的逻辑关系,可协助我们掌握问题的整体面貌,有脉络地思考问题的核心。大前研一 在其<<思考的技术>>一书里,强调金字塔结构(即议题树结构)的威力,他说:
“金字塔结构是导出问题解决对策必用的逻辑思考关键枢轴。”
“金字塔结构的根基,是源于MECE的概念,… 不论多么庞大的资料、多么复杂的议题,我们都可以应用MECE的思维方式,将其分类整理,然后从某些资料中找出证据导出结论,再把这个结论当作寻找下一个证据的数据……这种层层累积的方法,就是金字塔结构。”
4.2 透过跌代(Iteration),持续对议题进行<检验-否证>,并激发架构的创意
迭代的起步
麦肯锡人员最常用来分解问题的工具是逻辑树(Logic Tree),在面对复杂问题时,他们会先将问题中独立的议题(Issue)分离开来,分阶层而将之组织起来,呈现为一棵逻辑树,称为议题树形图,或简称为议题树。此树形图就跟一般的系统架构图一样,借着简化的方式呈现真实世界的要素,协助您掌握问题的整体面貌,有脉络地思考问题的核心。如果从问题分解出来的议题能满足MECE条件,将可避免遗漏和混乱,而有效地从复杂混乱之中找出次序来。
议题树包含一系列有待检验其假设(Hypothesis)的议题,之后会更详细分析事实(Facts)来证实或推翻其假设。例如:

图-5. 展开议题树的第一阶(层)
符合MECE原则
不重复(Mutually Exclusive)就是每片树叶(Subissue)都不重迭。不遗漏(Collectively Exhaustive)就是整棵树不能有漏洞。
以MECE的思考态度来建构议题树,可让我们在分析过程中,能逐渐地排除走不通的路,只要经由分析而发现任何议题的假设被推翻了,就删除议题树上的该支干,如此越让对的路浮现出来,也让自己越来越确信走对路了。例如,分析一下问题,可知道已经来不及撤退了,所以<可以安全撤退吗?>议题的答案是『否』,该假设被推翻了。同样地,事实也显示兵力太悬殊,无法正面迎敌,所以<可以正面迎敌吗?>议题的答案是『否』,该假设被推翻了。
★ 不遗漏(CE: Collectively Exhaustive)
MECE的“CE” 企图涵盖整个问题的每一个角落,否则我们可能会错失有关真正问题核心的事实资料,减损了说服力,也得不到最有效的解决对策。透过检验假设之方式,发现走不通的路,就指示我们不必花时间去探索该议题攸关之事实了。因而麦肯锡一方面以CE企图涵盖全貌,又巧妙地运用检验假设方式去判断并省掉无谓的探索。因之,达到不必探索全部却能掌握真正的核心。
★ 不重复(Mutually Exclusive)
MECE的“ME” 促使我们以不同的角度看问题,以互为独立的议题来将问题攸关之事实与予分割为独立的群组,让检验假定之机制能在发现走不通的路,能指示我们不必花时间去探索该议题攸关之事实。反之,当议题有重迭而混淆不清时,检验假定之机制就难以发挥了。例如,当<粮食足够吗?>议题之假设已经被推翻了,之后再检验<兵力足够防守吗?>议题时又必须分析粮食存量等事实,结果先前因<粮食足够吗?>议题之假设已经被推翻而省下来的深入探索的精力又被花掉了,而且可能在不同议题中,不断重复分析粮食存量等事实,则检验假定之机制就完全失灵了。
于是,我们从上图而观之,呈现出结论是:孔明走投无路了。其实不然,那是因为上图的议题树形图没有合乎MECE的条件,导致有所遗漏,而产生错误的结论。依循MECE原则而修正如下图:

图-6. 符合MECE原则的第一阶层
持续进行<检验-否证>
刚才说过了,MECE的“CE” 企图涵盖整个问题的每一个角落,否则我们可能会错失有关真正问题核心的事实资料,减损了说服力,也得不到最有效的解决对策。
MECE的“ME” 促使我们以不同的角度看问题,以互为独立的议题来将问题攸关之事实与予分割为独立的群组,让检验假定之机制能在发现走不通的路,能指示我们不必花时间去探索该议题攸关之事实。反之,当议题有重迭而混淆不清时,检验假定之机制就难以发挥了。例如,有个Issue-1涵盖了Issue-2,检验假设之机制推翻了Issue-2的假设,就可以省去探索Issue-2底下各子议题攸关之事实了,然而Issue-1涵盖了Issue-2,探索Issue-1攸关之事实时,必须探索原来Issue-2所惕除的事实,因此Issue-2所排除对某群事实之探索,并未对整体之节省做出贡献。因而折损了检验假设机制的效果。
现在,我们就针对上图的议题树,来进行<检验-否证>的动作。以MECE的思考态度来建构议题树,可让我们在分析过程中,能逐渐地排除走不通的路,只要经由分析而发现任何议题的假设被推翻了,就删除议题树上的该支干,如此越让对的路浮现出来,也让自己越来越确信走对路了。例如,分析一下问题,可知道已经来不及撤退了,所以<可以安全撤退吗?>议题的答案是『否』,该假设被推翻了。同样地,事实也显示兵力太悬殊,无法正面迎敌,所以<可以正面迎敌吗?>议题的答案是『否』,该假设被推翻了。如下图:

图-7. 进行<检验-否证>的动作
展开下一阶层的议题
如果所提的假设议题没有被否证,就必须进行更多更细腻的分析,直到有信心认定自己的假设绝对不会错,或错误的可能性微乎其微为止。例如,针对没有被删除的议题,进行另一次新的跌代(Iteration),展开下一阶层的议题,如下图:

图-8. 展开下一阶层的议题
一旦新层级的子议题也符合MECE了,就进行进行<检验-否证>动作。分析一下问题,可知道已经没有足够粮食了,所以「粮食足够吗?」议题的答案是『否』,也连带推翻「可以固守城内吗?」议题之假设了。如下图:

图-9. 麦肯锡的树状议题架构(又称议题树)
当「粮食足够吗?」议题之假设已经被推翻了,也连带推翻「可以固守城内吗?」议题之假设了;就不必费神去分析树和检验「兵力足够防守吗?」议题了。CE确保一颗完整的树,ME确保每一个树枝都是独立的。检验假设之机制让我们很智慧地检验树枝,被否定掉的树枝就整枝摘掉,不必深入探究更细小的枝叶。所以MECE的态度思考每一件事,将有关的要素连结起来,成为一棵完整的树,检验假设之机制让您智慧地摘掉无用的树枝,您就不必以相同的深度去探索它们,因而是个简洁有效的思考途径。
最后,剩下<空城计>议题没有被否证,于是针对该议题,而展开新一次的跌代,展开下阶层的议题树,力求MECE,并进行<检验-否证>动作。持续跌代(循环下去)。
4.3 结语
金字塔结构(即议题树结构)是源自麦肯锡(Mckinsey)顾问公司的MECE(Mutually Exclusive, Collectively Exhaustive)的概念,MECE就是「不重复,不遗漏」的意思。如果从Whole-Part角度来看,就是把一个整体(Whole)切分为多个部份(Part),这些部分之间彼此独立而不重迭(Mutually Exclusive),而这些部分组合起来又呈现出一个整体,毫无遗漏(Collectively Exhaustive)。麦肯锡人员最常用来分解问题的工具是逻辑树(Logic Tree),在面对复杂问题时,他们会先将问题中独立的议题(Issue)分离开来,分阶层而将之组织起来,呈现为一棵逻辑树,称为议题树形图,或简称为议题树。此树形图就跟一般的系统架构图一样,借着简化的方式呈现真实世界的要素,协助您掌握问题的整体面貌,有脉络地思考问题的核心。如果从问题分解出来的议题能满足MECE条件,将可避免遗漏和混乱,而有效地从复杂混乱之中找出次序来。议题树包含一系列有待检验其假设(Hypothesis)的议题,之后会更详细分析事实(Facts)来证实或推翻其假设。
麦肯锡的MECE模式是一种<假定驱动问题解决方法>(Hypothesis-Driven Problem Solving)。对于架构师或设计师而言,这是很有用的方法。因为,架构师们常常要先大胆假定客户、老板、或团队的期望是正确的,然后小心求证(有时很容易否决掉)。例如,三国时代刘备的期望:统一天下。孔明在<<隆中对>>里,就把它当一个大胆的假定,然后小心求证,根据事实而做了结论:<操拥兵百万,挟天子以令诸侯,不可与之争峰也>。于是否决了这项假定。接着,还删除了刘备的第二项愿望:二分天下。这是架构师天天在做的思维活动。
相关文章:
~ end ~



