迷宫问题求解之“A*搜索”(二)
摘要:在迷宫问题求解之“穷举+回溯”(一)这篇文章中采用“穷举+回溯”的思想,虽然能从迷宫的入口到出口找出一条简单路径,但是找出来的不是最优路径。因此本文采用A*搜索算法,求解迷宫问题的最优路径。
1 A*搜索算法简介
A*搜索算法是一种启发式搜索算法。所谓启发式搜索算法,就是在盲目搜索算法中加入一个启发函数,在当前节点搜索完毕后,通过这个启发函数来进行计算,选择代价最少的节点作为下一步搜索的节点。通过这样的方式就能够找到最优解。
DFS,BFS这两种搜索方式都属于盲目的搜索方式,它不会在选择下一个节点的时候进行代价计算,而是按照一个固定的方式选择,这样在运气不好的情况,会对所有节点进行遍历。
A*搜索算法的核心就在于如何设计一个好的启发函数,启发函数的表达形式一般如下:
$$
f(n)=g(n)+h(n)
$$
其中$f(n)$是每个节点可能的估值或者代价值,它由两部分组成。
- $g(n)$:它表示从起点到搜索点的代价。
- $h(n)$:它表示从搜索点到目标点的代价,$h(n)$设计的好坏,直接影响到该A*算法的效率。
一种具有$f(n)=g(n)+h(n)$策略的启发式算法能成为A*算法的充分条件是:
-
搜索树上存在着从起始点到终了点的最优路径。
-
问题域是有限的。
-
所有结点的子结点的搜索代价值都大于零。
-
h(n)=<h*(n) (h*(n)为实际问题的代价值)。
很显然,1,2,3点都很容易满足的。关键是设计一个好的$h(n)$函数。
2 A*搜索算法描述
A*算法的流程如下:
A*搜索算法需要两个额外的存储空间,OPEN表和CLOSE表。
-
初始化OPEN和CLOSE表,将开始节点(开始节点的H和G的值都视为0)放入OPEN表中。
-
重复下面步骤:
(循环)2.1 在开始列表中查找具有最小F值的节点,并把查找到的节点作为当前节点; 2.2 把当前节点从OPEN列表中删除,并加入到CLOSE列表中; 2.3 对当前节点相邻的每一个节点依次执行以下步骤:`(遍历)` **i **如果相邻节点不可通行或者该节点已经在CLOSE列表中,则什么操作也不执行; **ii **如果该相邻节点不在OPEN列表中,则将该节点添加到OPEN列表中,`并将该相邻节点的父节点设置当前节点`,同时计算保存相邻节点的F值;**iii **如果该相邻节点在OPEN表中, 则判断若经由当前节点到达该相邻节点的F值是否小于原来保存的F值,若小于,则将该相邻节点的父节点设为当前节点,并重新设置该相邻节点的F值. 2.4 若当终点节点被加入到开发列表作为待检验节点时,表示路径已找到,此时应终止循环;若当开放列表为空,表示没有中开始节点到终点节点的路径,此时循环结束; -
循环终止后,从终点节点开始沿着父节点往前遍历,从后到前输出搜索的路径。
其中,步骤2.3 ii中的红色部分尤为重要,设置相邻节点的父节点为当前节点是为了记录从起始节点到终止节点路径,方便搜索到了终点节点后进行路径输出。
在采用A* 算法对迷宫路径求解中,$g(n)$和$h(n)$函数都采用曼哈顿距离,曼哈顿距离代表两个点在标准坐标系上的绝对轴距总和。
$$
d(i,j)=|x1-x2|+|y1-y2|
$$
即每次获取的当前通道块,都会对其到入口通道快和出口通道块的曼哈顿距离进行计算。求算当前通道块的F值进行保存。该函数满足启发式算法成为A*算法的充分条件的1,2,3,4。
还需要注意的一点是:使用A*求解迷宫路径算法中,需要把2.3步骤下面的遍历操作进行更改,如下:
i 如果相邻节点不可通行或者该节点已经在CLOSE或者OPEN列表中,则什么操作也不执行。
ii 如果该相邻节点不在OPEN和CLOSE列表中,则将该节点添加到OPEN列表中,
并将该相邻节点的父节点设置当前节点,同时计算保存相邻节点的F值。
在迷宫求解中使用A*搜索算法不需要去更新OPEN表中的已存在节点的F值,因为每个节点的位置都是确定的,所以曼哈顿距离就固定的。如果是带权值的路网求解最短路径,那么就需要去更新OPEN表中节点的F值,如Dijkstra算法。
3 程序实现
下面使用使用c#语言,实现A*算法求解迷宫最优的路径。关键代码如下:
3.1 节点实体类
class PathNode
{
public PathNode(int row, int col)
{
this.Row = row;
this.Col = col;
}
public int Row;
public int Col;
public int F=int.MaxValue;
public PathNode Father=null;//该节点的前继节点
}
3.2 A*搜索类
class AStartSolution
{
int [,]map;
int startX;
int startY;
int endX;
int endY;
public AStartSolution (int [,]map,int startX,int startY,int endX,int endY)
{
this.map=map;
this.startX =startX;
this.startY=startY;
this.endX=endX;
this.endY=endY ;
}
/*路径寻找*/
public PathNode FindPath()
{
PathNode endNode = null;//终点
List<PathNode> openList = new List<PathNode>();
List<PathNode> closeList = new List<PathNode>();
//把起点放入open列表中
PathNode startNode = new PathNode(startX, startY);
openList.Add(startNode);
int tryCount = 0;
while (openList.Count != 0)
{
tryCount++;
PathNode curMinFNode = GetMinFPathNode(openList);
openList.Remove (curMinFNode );//从open列表中移除
closeList .Add (curMinFNode );//加入到close列表中
if (curMinFNode.Row == endX && curMinFNode.Col == endY)//当前节点是目标节点
{
endNode = curMinFNode;
break;
}
else//搜索4个方向并进行处理
{
//东
HandleChildNode(curMinFNode, curMinFNode.Row, curMinFNode.Col + 1, openList, closeList);
//南
HandleChildNode(curMinFNode, curMinFNode.Row+1, curMinFNode.Col, openList, closeList);
//西
HandleChildNode(curMinFNode, curMinFNode.Row, curMinFNode.Col-1, openList, closeList);
//北
HandleChildNode(curMinFNode, curMinFNode.Row-1, curMinFNode.Col, openList, closeList);
}
}
return endNode;
}
/*处理每个方向的子节点*/
private void HandleChildNode(PathNode curMinFNode,int row, int col, List<PathNode> openList, List<PathNode> closeList)
{
PathNode child = null;
if (Pass(row, col))//能通过
{
child = new PathNode(row, col);
if (!IsExistList(child, closeList) && !IsExistList(child, openList))//
{
child.F = GetF(row,col);
child.Father = curMinFNode;
openList.Add(child);
}
}
}
private PathNode GetMinFPathNode(List<PathNode> openList)
{
int minF= openList.Min(node =>node.F);
foreach (PathNode node in openList)
{
if (node.F == minF)
{
return node;
}
}
return null;
}
/*该通道块是否可通行*/
private bool Pass(int row,int col)
{
int rowCount = map.GetLength(0);
int colCount = map.GetLength(1);
//边界判断
if (row >= 0 && row < rowCount && col >= 0 && col < colCount)
{
//障碍判断
if (map[row, col] == 2)
{
return false;
}
else
{
return true;
}
}
else
{
return false;
}
}
/*当前通道块是否在OPEN或者CLOSE表中*/
private bool IsExistList(PathNode childNode, List<PathNode> list)
{
foreach (PathNode node in list)
{
if (node.Row == childNode.Row && node.Col == childNode.Col)
{
return true;
}
}
return false;
}
/*计算当前节点的F值*/
private int GetF(int curRow, int curCol)
{
int g = Math.Abs(startX - curRow) + Math.Abs(startY - curCol);
int h = Math.Abs(endX - curRow) + Math.Abs(endY - curCol);
return g + h;
}
}
3.3 与“穷举+回溯”算法的效果比较
采用同样的迷宫地图比较两种算法查找的路径,上结果图代表“穷举+回溯,下结果图代表本程序。
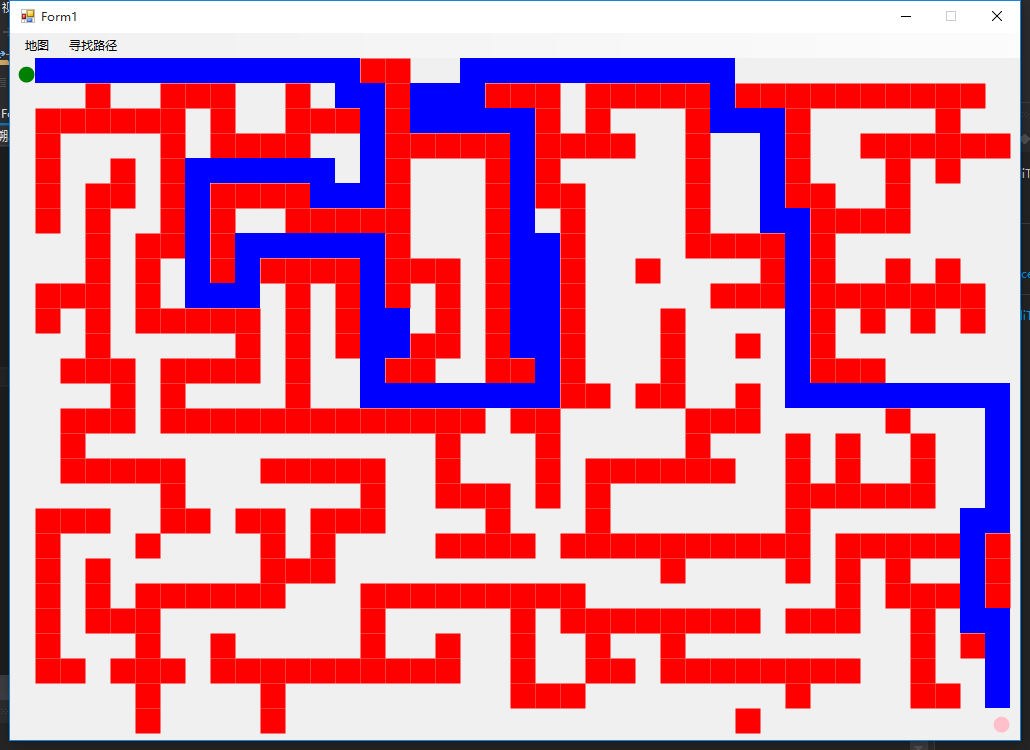
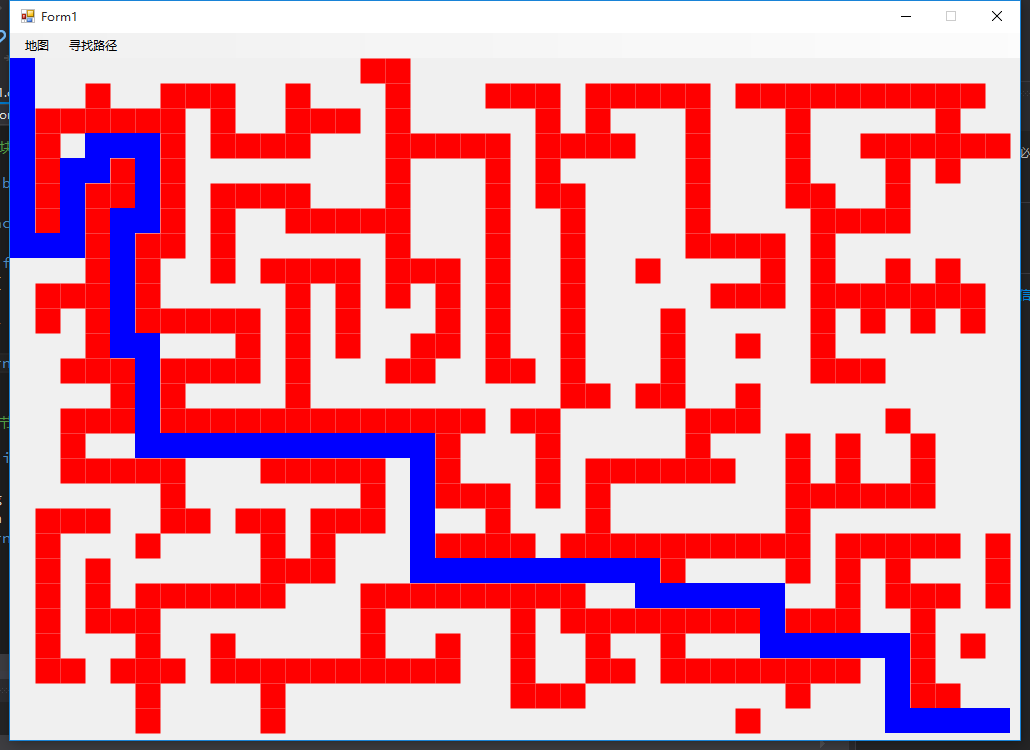
4 总结
通过上面的比较可以发现,A*搜索算法寻找的路径比“穷举+回溯”算法的要短很多,和我设计迷宫地图时所想的路径是一致,是一条最优的路径。
5 资源和参考资料
参考资料:
莫水千流的博文A星寻路算法介绍
西芒xiaoP的博文A*搜索算法
yueming的博文A*路径寻找算法入门
源码地址:


