从统计看机器学习(一) 一元线性回归

　　从统计学的角度来看，机器学习大多的方法是统计学中分类与回归的方法向工程领域的推广。

　　“回归”(Regression)一词的滥觞是英国科学家Francis Galton(1822-1911)在1886年的论文[1]研究孩子身高与父母身高之间的关系。观察1087对夫妇后，得出成年儿子身高=33.73+0.516*父母平均身高（以英寸为单位）.他发现孩子的身高与父母的身高相比更加温和：如果父母均非常高，那么孩子身高更倾向于很高但比父母矮；如果父母均非常矮，那么孩子身高更倾向于很矮但比父母高。这个发现被他称作"回归到均值"(regression to the mean).这也说明了的回归模型是软模型，回归模型更多的刻画了事物间的相关性而非因果性，它并不像物理模型或是一些函数（例如开普勒行星运动定律）那样严格苛刻。

1.从一元线性回归说起

　　我们判断体重是否合理时，却要先量量自己的身高。因为无论在生理角度还是审美角度，体重与身高是有关系的。通常可认为人体是均匀的，即身高与体重间的关系是线性的，那么我们无非希望建立一个一元线性回归模型

y=β₀+β₁x+ε,

x是当前的身高、ε是误差项，β₀与β₁是两个常数，通常认为每个身高下的ε都是独立的，且服从均值为0,方差为σ²的正态分布，记作ε-i.i.d~N(0,σ²).由于存在误差，当前身高x下的体重y,记作y|x,同样存在y|x~N(β₀+β₁x,σ²),因此我们将自己的身高x带入，就可以得到该身高下体重均值，并且有99.74%的把握认为该身高下，体重应该在(β₀+β₁x-3σ,β₀+β₁x+3σ)之间。当然，如果偏离了这个区间，体重就是不标准的，但是，这也要求σ的值不能太大。

　　一元线性回归就是要通过样本数据估计出β₀与β₁这两个常数的取值。当然，这是个仁者见仁、智者见智的问题，体重偏瘦的人为了保持身材，不希望有胖子的数据干扰模型；胖子会为了控制体重仅选择身高-体重最标准的人数据。当然，考虑女生身高与体重关系时选择男生的数据也是不合理的。我们依据自己的标准，选择不同身高下n个人的身高-体重数据(x₁, y₁), (x₂, y₂) ,…, (x_n, y_n),用最小二乘法得到β₀、β₁的估计值:

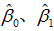
由于样本数据是我们按照规则挑选出来的，可以认为几乎不存在噪声数据，即σ的值不会太大，因此，当前身高下标准的体重范围也会缩小，使得模型更加精准有效。这样使用最小二乘法得到经验回归方程，即得到这样的一条直线

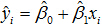是安全的。经验回归方程对样本中的任意的身高x_i的都能给出体重的估计值,体重的真实值与估计值的差称为真实的残差

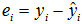由于残差存在正负，为了累计残差的效果，将全部样本点的残差进行平方再求和就得到了残差平方和。最小二乘法就是求解让残差平方和达到最小的优化问题。最小二乘法是让经验回归模型对全体样本的冲突达到最小，即使经验回归模型不经过样本中的任意一个点，但它会经过样本的均值点

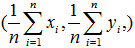
2.模型参数的估计过程

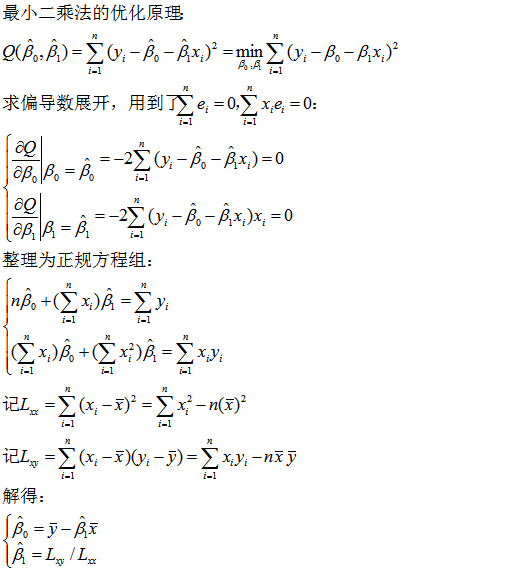
3.最小二乘估计的性质

首先，最小二乘估计是线性的。β₀,β₁的估计值是y_1,y₂,…,y_n的线性组合。同时，该估计是无偏的，即β₀,β₁的估计值的期望分别与β₀,β₁相同。

考虑模型是否有效，我们就要求估计值的方差

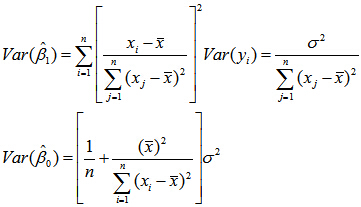
综上，对于给定的x₀,y₀的估计值服从与以下正态分布

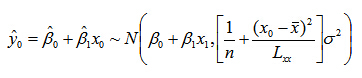
　　这说明了在经验回归模型中，不同x_i的估计值是无偏的，但方差大小一般不同。最小二乘法是唯一方差最小的无偏估计，也就是说，在全体的无偏模型中，最小二乘法的估计效果是最好的。从y₀的估计值分布中我们可以看出，如果想减小模型的方差，就要扩大样本容量，即增大n的值。同时，尽可能使样本的分散以增大L_xx.回到上面的体重-身高建模问题，如果选择不同身高、相同性别且体重-身高比例均为标准的人，那么运用最小二乘法很容易估计出该性别下最标准体重-身高的线性关系。

 

[1]Regression towards mediocrity in hereditary stature. Francis Galton, Journal of the Anthropological Institute, 1886, 15: 246 – 263