NOI 2012 魔幻棋盘 | 二维差分 + 二维线段树
题目:luogu 2086
二维线段树,按套路差分原矩阵,gcd( x1, x2, ……, xn ) = gcd( xi , x2 - x1 , ……, xn - xn-1 ),必须要有一个原数 xi,恰好每次询问都包含一个固定点 ( X , Y ),差分以它为中心就可以保证它是原值。以 e 为中心的二维差分如图。
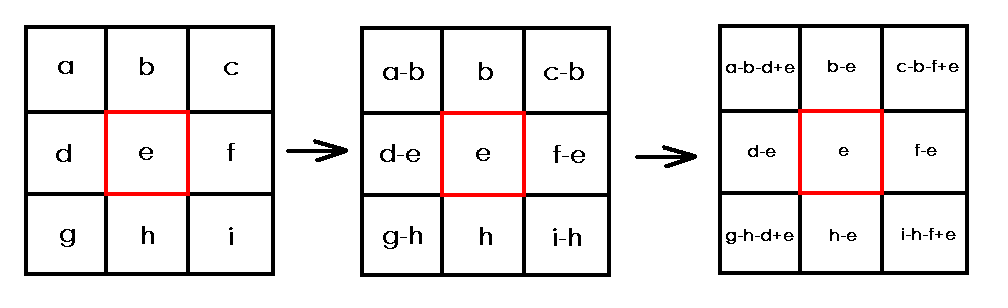
对于一维序列,修改区间 [ l , r ] 只需修改差分后的 l 和 r + 1 两点。那么对于二维,差分后的修改如下所示:
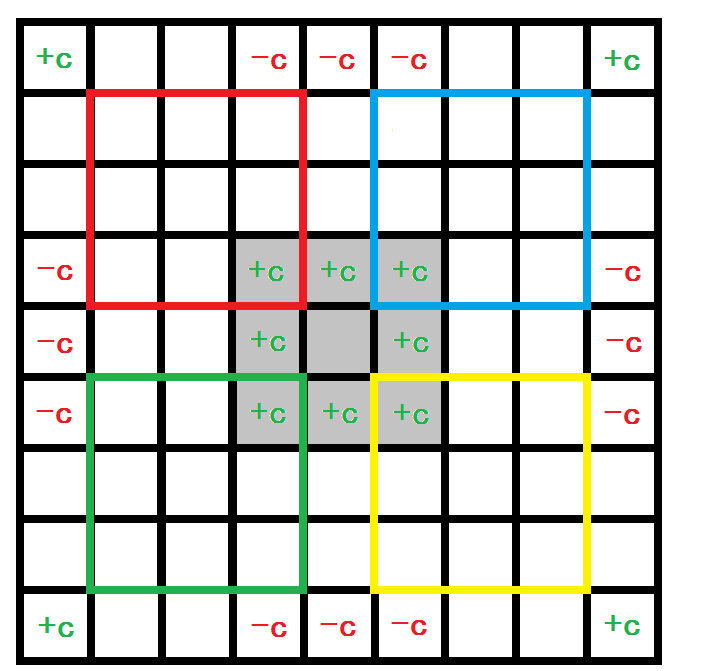
中间的灰色格子为守卫者所在地(为方便表示多个区域把它拆成了 9 格),以它为差分中心,若修改矩阵在它的右下方,即黄色区域,设它的左上角坐标为 ( x1, y1),右下角坐标 ( x2, y2 ),则需在 ( x1, y1 ) 处 + c,( x1, y2+1 ) 处 - c,( x2+1, y1 ) 处 - c,( x2 + 1, y2 + 1) 处 +c。
其他区域同理。再加上守卫者正上方、正下方、正左方、正右方的区域,一共 8 种情况。如果一个修改矩阵包含多个区域,就将其划分为若干个子矩阵处理。
这样就将巨慢的区间修改转换成了单点修改,每修改完一个点,pushup( ) 维护 gcd 即可。
另外读入的时候,500000 * 500000 的二维数组是开不了的,需要动态分配内存;或者开一个 500000 的一维数组读入,判断每一行的末端在哪里。
讨论的时候有些麻烦,下面列一下大致的情况:(黄色表示修改的区域,绿色加, 红色减)
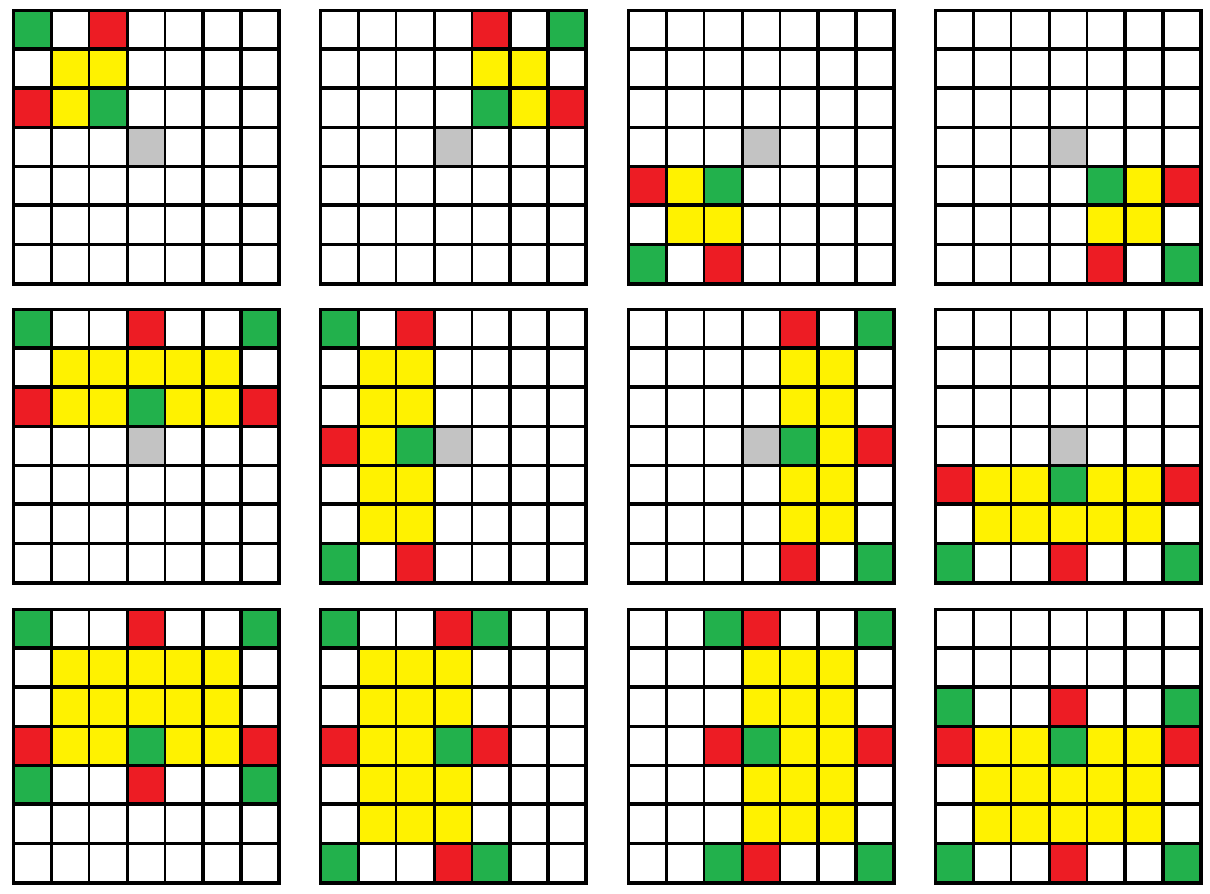
仔细观察后,发现可分为三种情况:① 包含守卫者 ( X , Y );② 包含 X 行或 Y 列;③ 只包含左上或左下、右上或右下区域。
细节诸多:
差分的时候不能用原数组减,因为前面的值会变,需要另开一个数组保存;
返回 gcd 的时候要取绝对值;二维线段树内层空间要开大。
1 #include <cstdio> 2 #include <string> 3 4 const int N = 500005; 5 typedef long long ll; 6 7 int n, m; ll a[N], b[N]; 8 9 ll read() { 10 ll x = 0, f = 1; 11 char c = getchar(); 12 while (!isdigit(c)) { 13 if (c == '-') f = -1; 14 c = getchar(); 15 } 16 while (isdigit(c)) { 17 x = (x << 3) + (x << 1) + (c ^ 48); 18 c = getchar(); 19 } 20 return x * f; 21 } 22 23 ll abs(ll x) { 24 if (x >= 0) return x; return -x; 25 } 26 27 ll gcd(ll x, ll y) { 28 if (y) return gcd(y, x % y); return abs(x); 29 } 30 31 struct inNode { 32 ll val; 33 inNode *ls, *rs; 34 inNode() : val(0), ls(NULL), rs(NULL) {} 35 } inPool[N << 2]; 36 37 inNode *newInNode () { 38 static int cnt = 0; 39 return &inPool[++cnt]; 40 } 41 42 void buildY(inNode *&cur, int l, int r, int x) { 43 if (!cur) cur = newInNode(); 44 if (l == r) cur->val = a[(x - 1) * m + l]; 45 else { 46 int mid = l + ((r - l) >> 1); 47 buildY(cur->ls, l, mid, x); 48 buildY(cur->rs, mid + 1, r, x); 49 cur->val = gcd(cur->ls->val, cur->rs->val); 50 } 51 } 52 53 void updateY(inNode *&cur, int l, int r, int y, ll val) { 54 if (l == r) cur->val += val; 55 else { 56 int mid = l + ((r - l) >> 1); 57 if (y <= mid) updateY(cur->ls, l, mid, y, val); 58 else updateY(cur->rs, mid + 1, r, y, val); 59 cur->val = gcd(cur->ls ? cur->ls->val : 0, cur->rs ? cur->rs->val : 0); 60 } 61 } 62 63 ll queryY(inNode *&cur, int l, int r, int y1, int y2) { 64 if (y1 <= l && r <= y2) return cur->val; 65 int mid = l + ((r - l) >> 1); ll res = 0; 66 if (y1 <= mid) res = gcd(res, queryY(cur->ls, l, mid, y1, y2)); 67 if (mid < y2) res = gcd(res, queryY(cur->rs, mid + 1, r, y1, y2)); 68 return res; 69 } 70 71 struct outNode { 72 inNode *root; 73 outNode *ls, *rs; 74 outNode() : root(NULL), ls(NULL), rs(NULL) {} 75 } outPool[N << 2], *root; 76 77 outNode *newOutNode() { 78 static int cnt = 0; 79 return &outPool[++cnt]; 80 } 81 82 void maintain(inNode *&cur, inNode *&lc, inNode *&rc, int l, int r) { 83 if (!cur) cur = newInNode(); 84 if (l == r) cur->val = gcd(lc->val, rc->val); 85 else { 86 int mid = l + ((r - l) >> 1); 87 maintain(cur->ls, lc->ls, rc->ls, l, mid); 88 maintain(cur->rs, lc->rs, rc->rs, mid + 1, r); 89 cur->val = gcd(cur->ls->val ,cur->rs->val); 90 } 91 } 92 93 void buildX(outNode *&cur, int l, int r) { 94 if (!cur) cur = newOutNode(); 95 if (l == r) buildY(cur->root, 1, m, l); 96 else { 97 int mid = l + ((r - l) >> 1); 98 buildX(cur->ls, l, mid); 99 buildX(cur->rs, mid + 1, r); 100 maintain(cur->root, cur->ls->root, cur->rs->root, 1, m); 101 } 102 } 103 104 void change(inNode *&cur, int l, int r, int y, ll val) { 105 if (l == r) cur->val = val; 106 else { 107 int mid = l + ((r - l) >> 1); 108 if (y <= mid) change(cur->ls, l, mid, y, val); 109 else change(cur->rs, mid + 1, r, y, val); 110 cur->val = gcd(cur->ls ? cur->ls->val : 0, cur->rs ? cur->rs->val : 0); 111 } 112 } 113 114 void updateX(outNode *&cur, int l, int r, int x, int y, ll val) { 115 if (x <= 0 || y <= 0 || x > n || y > m) return; 116 if (l == r) updateY(cur->root, 1, m, y, val); 117 else { 118 int mid = l + ((r - l) >> 1); ll lv = 0, rv = 0; 119 if (x <= mid) updateX(cur->ls, l, mid, x, y, val); 120 else updateX(cur->rs, mid + 1, r, x, y, val); 121 if (cur->ls) lv = queryY(cur->ls->root, 1, m, y, y); 122 if (cur->rs) rv = queryY(cur->rs->root, 1, m, y, y); 123 change(cur->root, 1, m, y, gcd(lv, rv)); 124 } 125 } 126 127 ll queryX(outNode *&cur, int l, int r, int x1, int x2, int y1, int y2) { 128 if (x1 <= l && r <= x2) return queryY(cur->root, 1, m, y1, y2); 129 int mid = l + ((r - l) >> 1); ll res = 0; 130 if (x1 <= mid) res = gcd(res, queryX(cur->ls, l, mid, x1, x2, y1, y2)); 131 if (mid < x2) res = gcd(res, queryX(cur->rs, mid + 1, r, x1, x2, y1, y2)); 132 return res; 133 } 134 135 int main() { 136 n = read(), m = read(); int X = read(), Y = read(), T = read(); 137 for (int i = 1; i <= n * m; ++ i) a[i] = read(); 138 for (int i = 1; i <= n * m; ++ i) { 139 if ((i - 1) % m + 1 < Y) b[i] = a[i] - a[i + 1]; 140 else if ((i - 1) % m + 1 > Y) b[i] = a[i] - a[i - 1]; 141 else b[i] = a[i]; 142 } 143 for (int i = 1; i <= n * m; ++ i) { 144 if ((i - 1) / m + 1 < X) a[i] = b[i] - b[i + m]; 145 else if ((i - 1) / m + 1 > X) a[i] = b[i] - b[i - m]; 146 else a[i] = b[i]; 147 } 148 buildX(root, 1, n); 149 while (T--) { 150 int opt = read(), x1 = read(), y1 = read(), x2 = read(), y2 = read(); 151 if (opt == 0) { 152 x1 = X - x1, x2 = X + x2, y1 = Y - y1, y2 = Y + y2; 153 printf("%lld\n", queryX(root, 1, n, x1, x2, y1, y2)); 154 } else { 155 ll val = read(); 156 if (x1 <= X && x2 >= X && y1 <= Y && y2 >= Y) { //包含(X,Y) 157 updateX(root, 1, n, X, Y, val); 158 updateX(root, 1, n, x1 - 1, y1 - 1, val); 159 updateX(root, 1, n, x1 - 1, y2 + 1, val); 160 updateX(root, 1, n, x2 + 1, y1 - 1, val); 161 updateX(root, 1, n, x2 + 1, y2 + 1, val); 162 updateX(root, 1, n, x1 - 1, Y, -val); 163 updateX(root, 1, n, x2 + 1, Y, -val); 164 updateX(root, 1, n, X, y1 - 1, -val); 165 updateX(root, 1, n, X, y2 + 1, -val); 166 } else if (y1 <= Y && y2 >= Y) { //包含Y列 167 if (x1 < X) { //在(X,Y)上方 168 updateX(root, 1, n, x2, Y, val); 169 updateX(root, 1, n, x1 - 1, y1 - 1, val); 170 updateX(root, 1, n, x1 - 1, y2 + 1, val); 171 updateX(root, 1, n, x1 - 1, Y, -val); 172 updateX(root, 1, n, x2, y1 - 1, -val); 173 updateX(root, 1, n, x2, y2 + 1, -val); 174 } else { //在(X,Y)下方 175 updateX(root, 1, n, x1, Y, val); 176 updateX(root, 1, n, x2 + 1, y1 - 1, val); 177 updateX(root, 1, n, x2 + 1, y2 + 1, val); 178 updateX(root, 1, n, x2 + 1, Y, -val); 179 updateX(root, 1, n, x1, y1 - 1, -val); 180 updateX(root, 1, n, x1, y2 + 1, -val); 181 } 182 } else if (x1 <= X && x2 >= X) { //包含X行 183 if (y1 < Y) { //在(X,Y)左边 184 updateX(root, 1, n, X, y2, val); 185 updateX(root, 1, n, x1 - 1, y1 - 1, val); 186 updateX(root, 1, n, x2 + 1, y1 - 1, val); 187 updateX(root, 1, n, X, y1 - 1, -val); 188 updateX(root, 1, n, x1 - 1, y2, -val); 189 updateX(root, 1, n, x2 + 1, y2, -val); 190 } else { //在(X,Y)右边 191 updateX(root, 1, n, X, y1, val); 192 updateX(root, 1, n, x1 - 1, y2 + 1, val); 193 updateX(root, 1, n, x2 + 1, y2 + 1, val); 194 updateX(root, 1, n, X, y2 + 1, -val); 195 updateX(root, 1, n, x1 - 1, y1, -val); 196 updateX(root, 1, n, x2 + 1, y1, -val); 197 } 198 } else if (x1 < X && y1 < Y) { //左上区域 199 updateX(root, 1, n, x2, y2, val); 200 updateX(root, 1, n, x1 - 1, y1 - 1, val); 201 updateX(root, 1, n, x1 - 1, y2, -val); 202 updateX(root, 1, n, x2, y1 - 1, -val); 203 } else if (x1 < X && y1 > Y) { //右上区域 204 updateX(root, 1, n, x2, y1, val); 205 updateX(root, 1, n, x1 - 1, y2 + 1, val); 206 updateX(root, 1, n, x1 - 1, y1, -val); 207 updateX(root, 1, n, x2, y2 + 1, -val); 208 } else if (x1 > X && y1 < Y) { //左下区域 209 updateX(root, 1, n, x1, y2, val); 210 updateX(root, 1, n, x2 + 1, y1 - 1, val); 211 updateX(root, 1, n, x1, y1 - 1, -val); 212 updateX(root, 1, n, x2 + 1, y2, -val); 213 } else { //右下区域 214 updateX(root, 1, n, x1, y1, val); 215 updateX(root, 1, n, x2 + 1, y2 + 1, val); 216 updateX(root, 1, n, x1, y2 + 1, -val); 217 updateX(root, 1, n, x2 + 1, y1, -val); 218 } 219 } 220 } 221 return 0; 222 }

