APIO 2012 守卫 | 差分 / 线段树 + 贪心
题目:luogu 3634
首先把为 0 的区间删去,重新标号,可以差分也可以线段树。
把包含其他线段的线段删去,原因 1 是它没有用,原因 2 下面再说。然后,贪心选取最少的点来满足所有线段,即选取还没有点在上面的线段的右端点。如下图中选取的红色方格。
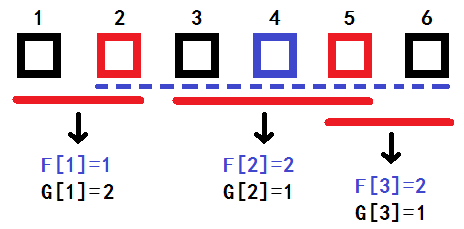
倘若不删去包含其他线段的线段,如上图中的蓝色虚线,我们在贪心选取点的时候,就会先扫到蓝线的左端点而后扫到第二条红线,按照规则,我们会选择蓝线的右端点 6 号点,接下来扫到第二条红线时,由于它上面并没有点被选取,所以又会选取它的右端点 5 号点,这样显然不是最优的,这就是第 2 个原因。
选完点后,从左往右扫,每扫到一个选取的点,如果该点不是必选的(覆盖它的线段 l ≠ r),就尝试若不选它是否可行,即选取它左边相邻的点,计算出选取这个点时的最少点数,计算方法如下。
如上图,用 F[ i ] 表示前 i 条线段需要选取的最少点数,G[ i ] 表示后 i 条线段需要选取的最少点数,假设现在我们尝试不选 5 号点,计算选取 4 号点时需要选取的最少点数,然后与 k 比较,方法是二分找出右端点最大且小于 4 的线段 x,找出左端点最小且大于 4 的线段 y,若 F[ x ] + G[ y ] + 1 大于 k 则尝试失败,说明先前点是必选的。
1 #include <cstdio> 2 #include <string> 3 #include <algorithm> 4 5 const int N = 100005; 6 7 struct line { 8 int l, r, f; 9 bool operator < (const line &cmp) const { 10 return l < cmp.l; 11 } 12 } a[N]; 13 14 int b[N], L[N], R[N], be[N], F[N], G[N]; 15 16 int read() { 17 int x = 0, f = 1; 18 char c = getchar(); 19 while (!isdigit(c)) { 20 if (c == '-') f = -1; 21 c = getchar(); 22 } 23 while (isdigit(c)) { 24 x = (x << 3) + (x << 1) + (c ^ 48); 25 c = getchar(); 26 } 27 return x * f; 28 } 29 30 int main() { 31 int n = read(), k = read(), m = read(); 32 for (int i = 1; i <= m; ++ i) { //差分标记为 0 的区间 33 a[i].l = read(), a[i].r = read(), a[i].f = read(); 34 if (a[i].f == 0) ++b[a[i].l], --b[a[i].r+1]; 35 } 36 int cur = 0, cnt = 0; 37 for (int i = 1; i <= n; ++ i) { //去除为 0 的区间并重新标号 38 cur += b[i]; 39 if (cur == 0) L[i] = R[i] = ++cnt, be[cnt] = i; 40 } 41 if (cnt == k) { //恰好满足 42 for (int i = 1; i <= cnt; ++ i) printf("%d\n", be[i]); 43 return 0; 44 } 45 L[n + 1] = n + 1; 46 for (int i = 1; i <= n; ++ i) 47 if (R[i] == 0) R[i] = R[i - 1]; 48 for (int i = n; i >= 1; -- i) 49 if (L[i] == 0) L[i] = L[i + 1]; 50 cnt = 0; 51 for (int i = 1; i <= m; ++ i) { 52 if (a[i].f == 0) continue; 53 int l = L[a[i].l], r = R[a[i].r]; 54 if (l <= r) a[++cnt].l = l, a[cnt].r = r; 55 } 56 std::sort(a + 1, a + cnt + 1); 57 int top = 0; 58 for (int i = 1; i <= cnt; ++ i) { //去除包含其他线段的线段 59 while (top && a[i].l >= L[top] && a[i].r <= R[top]) --top; 60 L[++top] = a[i].l, R[top] = a[i].r; 61 } 62 int l = n + 1, r = 0; 63 for (int i = 1; i <= top; ++ i) { //贪心选取最少的点 64 if (L[i] > r) F[i] = F[i - 1] + 1, r = R[i]; 65 else F[i] = F[i - 1]; 66 } 67 for (int i = top; i >= 1; -- i) { 68 if (R[i] < l) G[i] = G[i + 1] + 1, l = L[i]; 69 else G[i] = G[i + 1]; 70 } 71 bool ok = 0; 72 for (int i = 1; i <= top; ++ i) { //尝试不选 73 if (F[i] == F[i - 1]) continue; 74 if (L[i] == R[i]) { 75 printf("%d\n", be[R[i]]); 76 ok = 1; continue; 77 } 78 int l = 1, r = i - 1, x = 0, y = top + 1; 79 while (l <= r) { //二分查找 80 int mid = l + ((r - l) >> 1); 81 if (R[mid] < R[i] - 1) x = mid, l = mid + 1; 82 else r = mid - 1; 83 } 84 l = i + 1, r = top; 85 while (l <= r) { 86 int mid = l + ((r - l) >> 1); 87 if (L[mid] > R[i] - 1) y = mid, r = mid - 1; 88 else l = mid + 1; 89 } 90 if (F[x] + G[y] + 1 > k) { 91 printf("%d\n", be[R[i]]); 92 ok = 1; 93 } 94 } 95 if (!ok) puts("-1"); 96 return 0; 97 }


