二分图匹配 && Hopcroft - Carp 算法详解
二分图基本概念
最大匹配
集合X中有n个点,集合Y中有m个点,X与Y间共有E条边。
匈牙利算法 O(n*m)
思路引入 . jpg
每次从一个结点出发搜索匹配点,当且仅当搜到的结点未匹配或匹配后更优时,匹配。

1 #include<cstdio> 2 #include<string> 3 #include<cstring> 4 #include<vector> 5 6 const int N = 1000 + 10; 7 8 int n, m, e, mry[N]; 9 bool vis[N]; 10 std::vector <int> Q[N]; 11 12 int read() { 13 int x = 0, f = 1; 14 char c = getchar(); 15 while (!isdigit(c)) { 16 if (c == '-') f = -1; 17 c = getchar(); 18 } 19 while (isdigit(c)) { 20 x = (x << 3) + (x << 1) + (c ^ 48); 21 c = getchar(); 22 } 23 return x * f; 24 } 25 26 bool DFS(int u) { 27 int size = Q[u].size(); 28 for (int i = 0; i < size; ++ i) 29 if (!vis[Q[u][i]]) { 30 vis[Q[u][i]] = 1; 31 if (!mry[Q[u][i]] || DFS(mry[Q[u][i]])) { 32 mry[Q[u][i]] = u; 33 return 1; 34 } 35 } 36 return 0; 37 } 38 39 int main() { 40 n = read(), m = read(), e = read(); 41 for (int i = 1; i <= e; ++ i) { 42 int u = read(), v = read(); 43 if (u <= n && v <= m) Q[u].push_back(v); 44 } 45 int ans = 0; 46 for (int i = 1; i <= n; ++ i) { 47 memset(vis, 0, sizeof vis); 48 if (DFS(i)) ++ans; 49 } 50 printf("%d\n", ans); 51 return 0; 52 }
Hopcroft-Carp 算法 O(sqrt(n)*E)
由于网上对HC的讲解很少,因此我想在这里讲讲HC。
先附上代码:

1 struct Hopcroft_Carp { 2 int nx, ny, e, mx[N], my[N], dx[N], dy[N], dis; 3 bool used[N]; 4 std::vector<int> G[N]; 5 6 void in() { 7 nx = read(), ny = read(), e = read(); 8 for (int i = 1; i <= e; ++ i) { 9 int u = read(), v = read(); 10 if (u <= nx && v <= ny) 11 G[u].push_back(v); 12 } 13 } 14 15 bool BFS() { 16 std::queue<int> Q; 17 dis = INF; 18 memset(dx, -1, sizeof dx); 19 memset(dy, -1, sizeof dy); 20 for (int i = 1; i <= nx; ++ i) { 21 if (mx[i] == 0) Q.push(i), dx[i] = 0; 22 } 23 while (!Q.empty()) { 24 int u = Q.front(); Q.pop(); 25 if (dx[u] > dis) break; 26 int size = G[u].size(); 27 for (int i = 0; i < size; ++ i) { 28 int v = G[u][i]; 29 if (dy[v] == -1) { 30 dy[v] = dx[u] + 1; 31 if (my[v] == 0) 32 dis = dy[v]; 33 else 34 dx[my[v]] = dy[v] + 1, Q.push(my[v]); 35 } 36 } 37 } 38 return dis != INF; 39 } 40 41 bool DFS(int u) { 42 int size = G[u].size(); 43 for (int i = 0; i < size; ++ i) { 44 int v = G[u][i]; 45 if (!used[v] && dy[v] == dx[u] + 1) { 46 used[v] = 1; 47 if (my[v] != 0 && dy[v] == dis) continue; 48 if (my[v] == 0 || DFS(my[v])) { 49 my[v] = u, mx[u] = v; 50 return 1; 51 } 52 } 53 } 54 return 0; 55 } 56 57 int Maxmatch() { 58 int ans = 0; 59 while (BFS()) { 60 memset(used, 0, sizeof used); 61 for (int i = 1; i <= nx; ++ i) 62 if (mx[i] == 0 && DFS(i)) ++ ans; 63 } 64 return ans; 65 } 66 } HC;
增广路定义:依次经过 "未匹配点->未匹配边->匹配点->匹配边->匹配点->未匹配边->未匹配点……" ,以未匹配点为起点、以另一未匹配点为终点的路径。
算法核心:
(1) 每次寻找多条增广路。(2) 在一条增广路上,易证 "未匹配边 = 匹配边 + 1"。
增广时,只要交换增广路上的匹配边与未匹配边,就可以增加一条匹配边,减少一条未匹配边。
BFS:寻找增广路。
以X中一个未匹配点为起点,出发寻找增广路。用 dx[] 和 dy[] 分别记录X中和Y中结点在增广路中的层次。设起点u的层次dx[u]=0,与u相连的所有结点的层次dy[v]=1,以此类推,直至找到一个未匹配点,说明成功找到了一条增广路,用dis(初始值为无穷大)来记录这个未匹配点的层次,即这个增广路的长度;如果不存在增广路(寻找结束时dis值仍为无穷大)则说明已经达到最大匹配,返回主程序。重复多个这样的循环,找到多条增广路径。
DFS:在增广路上进行匹配尝试。(交换匹配边与未匹配边)
与匈牙利算法类似。唯一不同的是这种尝试是有方向地进行,沿着层次值+1的方向。其目的是将这条增广路上的匹配边与未匹配边交换,以增加一条匹配边。
优化 1:匈牙利算法对集合X中的每个点都进行DFS;HC在不存在增广路时终止循环。
优化 2:匈牙利算法在DFS(u)时,对每个能连到的点v都进行尝试;HC则巧妙设置数组 dx[] 和 dy[] 记录增广路,仅沿着增广路尝试。
优化 3:HC在BFS中是一次找出多条不相交的增广路,以提升效率。
我们用这里的图来跑一遍HC,发现最终的匹配边与匈牙利算法的不同:(数字为结点的层次值,pink边为匹配边)
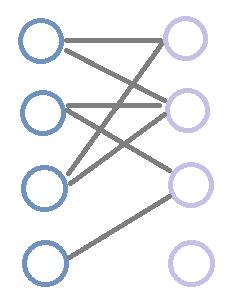
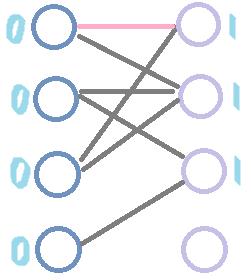
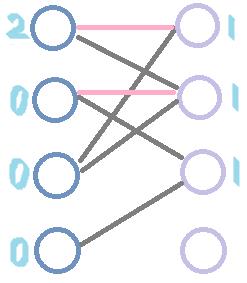
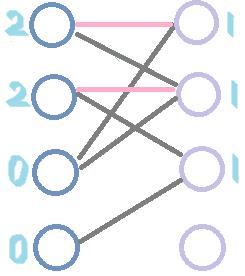
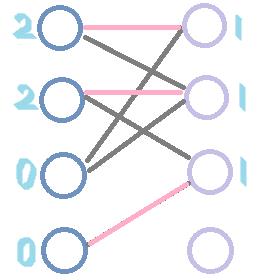
为什么会这样呢?根据两种算法的原理,易得出结论,请读者自己思考,这里不再赘述。
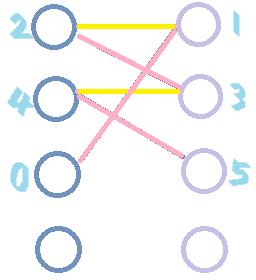
为了方便理解,我们对图精简化。pink边为匹配边,yellow边为反悔边。
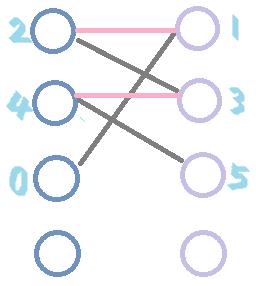
图(I)表示BFS的过程,当前已经完成两对匹配,从第三个结点出发,找到一条增广路径 0->1->2->3->4->5;
图(II)表示DFS的过程,沿增广路进行匹配尝试,比较两图容易看出匹配边与未匹配边的交换结果。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号