牛顿迭代法

     牛顿迭代法（Newton's method）又称为牛顿-拉夫逊（拉弗森）方法（Newton-Raphson method），它是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法。

牛顿迭代公式

    设r是\(f(x)=0\)的根，选取\(x_0\)作为r的初始近似值，过点\((x_0,f(x_0))\) ,做曲线 \(y=f(x)\)的切线L，L的方程为\(y=f(x_0)+f’(x_0)(x-x_0)\) ，求出L与x轴交点的横坐标

\[x_1=x_0-\frac{f(x_0)}{f’(x_0)}\]

    称\(x_1\)为r的一次近似值。过点\((x_1,f(x_1))\) 做曲线 \(y=f(x)\)的切线，并求该切线与x轴交点的横坐标

\[x_2=x_1-\frac{f(x_1)}{f’(x_1)}\]

    称\(x_2\)为r的二次近似值。重复以上过程，得r的近似值序列，其中，

\[x_{n+1}=x_n-\frac{f(x_n)}{f’(x_n)}\]

    称为r的\(n+1\)次近似值，上式称为牛顿迭代公式。

    用牛顿迭代法解非线性方程，是把非线性方程\(f(x)=0\)线性化的一种近似方法。把 \(f(x)\)在点 \(x_0\)的某邻域内展开成泰勒级数

\[f(x)=f(x_0)+f’(x_0)(x-x_0)+\frac{f’’(x_0)(x-x_0)^2}{2!}+…+\frac{f^{(n)}(x_0)(x-x_0)^n}{n!}+R_n(x)\]

     取其线性部分（即泰勒展开的前两项），并令其等于0，即 \(f(x_0)+f’(x_0)(x-x_0)=0\)，以此作为非线性方程 \(f(x)=0\)的近似方程，若\(f’(x_0)\neq0\)，则其解为

\[x_1=x_0-\frac{f(x_0)}{f’(x_0)}\]

     这样，得到牛顿迭代法的一个迭代关系式：

\[x_{n+1}=x_n-\frac{f(x_n)}{f’(x_n)}\]

    从下面的图中，我们可以看到牛顿迭代的几何意义，每次迭代，都会更加逼近\(f(x)=0\)的解。

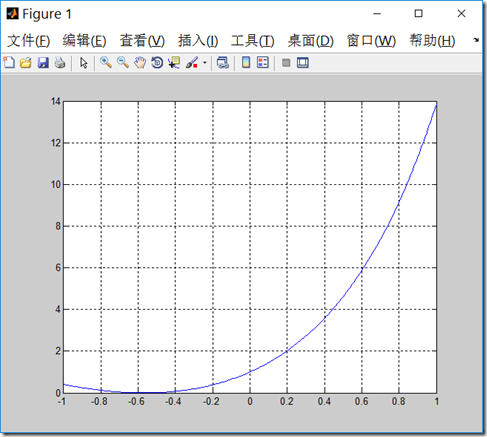
     下面用牛顿迭代法在matlib解出方程\(x^2+2xe^x+e^{2x}=0\)的根，首先画出函数的图像，猜测根的大致位置。

函数图像如下图所示：

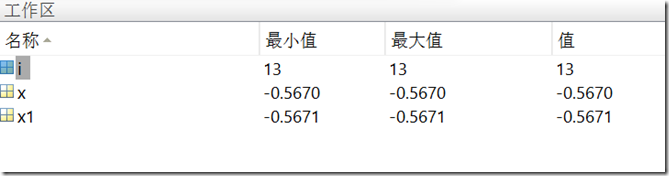
近似结果：

x=-1:0.01:1;
y= x.^2+2*x.*exp(x)+exp(2*x)
plot(x,y);
grid on;
clc;clear;
%syms x;
%diff(x^2+2*x*exp(x)+exp(2*x),x,1)
%clear;
x=0.0
for i=1:100
    x1=x-(x^2+2*x*exp(x)+exp(2*x))/(2*x + 2*exp(2*x) + 2*exp(x) + 2*x*exp(x))
    if(abs(x1-x)>0.0001)
        x=x1;
    else
        break;
    end
end
i