这一篇要总结的是树中的最后一种,即哈夫曼树,我想从以下几点对其进行总结:
1,什么是哈夫曼树?
2,如何构建哈夫曼树?
3,哈夫曼编码?
4,算法实现?
一,什么是哈夫曼树
什么是哈夫曼树呢?
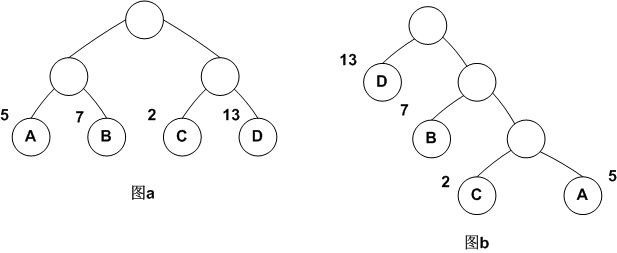
哈夫曼树是一种带权路径长度最短的二叉树,也称为最优二叉树。下面用一幅图来说明。
它们的带权路径长度分别为:
图a: WPL=5*2+7*2+2*2+13*2=54
图b: WPL=5*3+2*3+7*2+13*1=48
可见,图b的带权路径长度较小,我们可以证明图b就是哈夫曼树(也称为最优二叉树)。
二,如何构建哈夫曼树
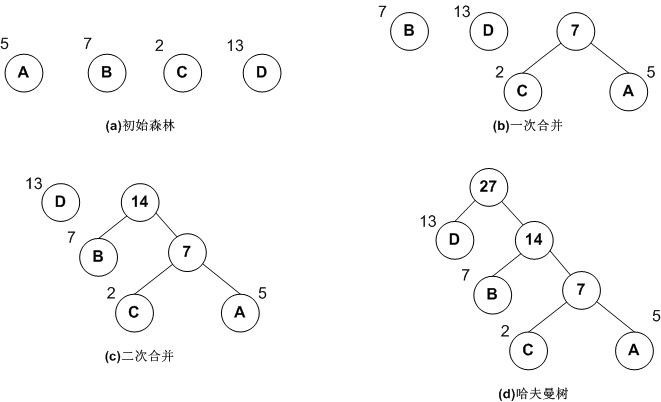
一般可以按下面步骤构建:
1,将所有左,右子树都为空的作为根节点。
2,在森林中选出两棵根节点的权值最小的树作为一棵新树的左,右子树,且置新树的附加根节点的权值为其左,右子树上根节点的权值之和。注意,左子树的权值应小于右子树的权值。
3,从森林中删除这两棵树,同时把新树加入到森林中。
4,重复2,3步骤,直到森林中只有一棵树为止,此树便是哈夫曼树。
下面是构建哈夫曼树的图解过程:
三,哈夫曼编码
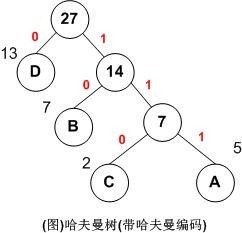
利用哈夫曼树求得的用于通信的二进制编码称为哈夫曼编码。树中从根到每个叶子节点都有一条路径,对路径上的各分支约定指向左子树的分支表示”0”码,指向右子树的分支表示“1”码,取每条路径上的“0”或“1”的序列作为各个叶子节点对应的字符编码,即是哈夫曼编码。
就拿上图例子来说:
A,B,C,D对应的哈夫曼编码分别为:111,10,110,0
用图说明如下:
记住,设计电文总长最短的二进制前缀编码,就是以n个字符出现的频率作为权构造一棵哈夫曼树,由哈夫曼树求得的编码就是哈夫曼编码。
四,算法实现
C#版:
namespace HuffTree.CSharp { class Program { static void Main(string[] args) { //四个叶子节点 int leafNum = 4; //赫夫曼树的节点总数 int totalNodes = 2 * leafNum - 1; //各叶子节点的权值 int[] weight = new int[] { 5,7,2,13}; //各叶子节点的值 string[] alphabet = new string[] { "A","B","C","D"}; //初始化赫夫曼树 HuffmanTree[] huffmanTree = new HuffmanTree[totalNodes].Select(p => new HuffmanTree() { }).ToArray(); //构建赫夫曼树 HuffmanTreeBLL.Create(huffmanTree,leafNum,weight); //赫夫曼编码 string[] huffmanCode = HuffmanTreeBLL.Coding(huffmanTree,leafNum); //打印结果 PrintResult(alphabet,huffmanTree,huffmanCode,leafNum); Console.ReadKey(); } /// <summary> /// 打印结果 /// </summary> /// <param name="alphabet"></param> /// <param name="huffmanTree"></param> /// <param name="huffmanCode"></param> /// <param name="leafNum"></param> private static void PrintResult(string[] alphabet,HuffmanTree[] huffmanTree,string[] huffmanCode,int leafNum) { if (alphabet.Count() < 1 || huffmanTree.Count() < 1 || huffmanCode.Count() < 1) return; for (int i = 0; i < leafNum; i++) { Console.WriteLine("字符:{0},权重值:{1},赫夫曼编码:{2}",alphabet[i],huffmanTree[i].Weight,huffmanCode[i]); } } } } namespace DS.BLL { /// <summary> /// 描述:赫夫曼树操作类 /// 作者:鲁宁 /// 时间:2013/9/17 18:14:33 /// </summary> public class HuffmanTreeBLL { /// <summary> /// 构建赫夫曼树 /// 思路:一步一步向上搭建 /// </summary> /// <param name="huffmanTree">待操作的赫夫曼树</param> /// <param name="leafNum">叶节点数量</param> /// <param name="weight">节点权重值</param> /// <returns>构建好的赫夫曼树</returns> public static HuffmanTree[] Create(HuffmanTree[] huffmanTree, int leafNum, int[] weight) { //获取赫夫曼树结点总数 int totalNodes = 2 * leafNum - 1; InitLeafNode(huffmanTree,leafNum,weight); //构造赫夫曼树(4个节点只需要3步就可以完成构建) for (int i = leafNum; i < totalNodes; i++) { //获取权重最小的两个叶子节点的下标 int minIndex1 = -1; int minIndex2 = -1; SelectNode(huffmanTree,i,ref minIndex1,ref minIndex2); huffmanTree[minIndex1].Parent = i; huffmanTree[minIndex2].Parent = i; huffmanTree[i].Left = minIndex1; huffmanTree[i].Right = minIndex2; huffmanTree[i].Weight = huffmanTree[minIndex1].Weight + huffmanTree[minIndex2].Weight; } return huffmanTree; } /// <summary> /// 赫夫曼编码 /// 思路:左子树为0,右子树为1,对应的编码后的规则是:从根节点到子节点 /// </summary> /// <param name="huffmanTree">待操作的赫夫曼树</param> /// <param name="leafNum">叶子节点的数量</param> /// <returns>赫夫曼编码</returns> public static string[] Coding(HuffmanTree[] huffmanTree, int leafNum) { string[] huffmanCode= new string[leafNum]; //当前节点下标 int current = 0; //父节点下标 int parent = 0; for (int i = 0; i < leafNum; i++) { string codeTemp = string.Empty; current = i; //第一次获取最左节点 parent = huffmanTree[current].Parent; while (parent != 0) { if (huffmanTree[parent].Left == current) codeTemp += "0"; else codeTemp += "1"; current = parent; parent = huffmanTree[parent].Parent; } huffmanCode[i] = new string(codeTemp.Reverse().ToArray()); } return huffmanCode; } /// <summary> /// 初始化叶节点 /// </summary> /// <param name="huffmanTree"></param> /// <param name="leafNum"></param> /// <param name="weight"></param> private static void InitLeafNode(HuffmanTree[] huffmanTree, int leafNum, int[] weight) { if (huffmanTree == null || leafNum<1 || weight.Count()<1) return; for (int i = 0; i < leafNum; i++) { huffmanTree[i].Weight = weight[i]; } } /// <summary> /// 获取叶子节点中权重最小的两个节点 /// </summary> /// <param name="huffmanTree">待操作的赫夫曼</param> /// <param name="searchNode">要查找的节点数</param> /// <param name="minIndex1"></param> /// <param name="minIndex2"></param> private static void SelectNode(HuffmanTree[] huffmanTree, int searchNode, ref int minIndex1, ref int minIndex2) { HuffmanTree minNode1 = null; HuffmanTree minNode2 = null; for (int i = 0; i < searchNode; i++) { //只查找独根树叶子节点 if (huffmanTree[i].Parent == 0) { //如果为null,则表示当前节叶子节点最小 if (minNode1 == null) { minIndex1 = i; minNode1= huffmanTree[i]; continue; } if (minNode2 == null) { minIndex2 = i; minNode2= huffmanTree[i]; //交换位置,确保minIndex1为最小 if (minNode1.Weight >= minNode2.Weight) { //节点交换 var temp = minNode1; minNode1 = minNode2; minNode2 = temp; //交换下标 var tempIndex = minIndex1; minIndex1 = minIndex2; minIndex2 = tempIndex; continue; } } if (minNode1 != null && minNode2 != null) { if (huffmanTree[i].Weight < minNode1.Weight) //注意,不能是“<=” { //将min1临时转存给min2 minNode2 = minNode1; minNode1 = huffmanTree[i]; //记录在数组中的下标 minIndex2 = minIndex1; minIndex1 = i; } else { if (huffmanTree[i].Weight < minNode2.Weight) { minNode2= huffmanTree[i]; minIndex2 = i; } } } } } } } /// <summary> /// 赫夫曼树存储结构 /// </summary> public class HuffmanTree { public int Weight { get; set; } //权值 public int Parent { get; set; } //父节点 public int Left { get; set; } //左孩子节点 public int Right { get; set; } //右孩子节点 } }
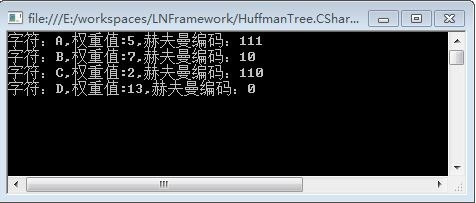
程序输出结果为: