MT【100】经典计数之分配问题

      注意：此讲适合联赛一试学生，以及参加清华北大等名校的自主招生的学生.

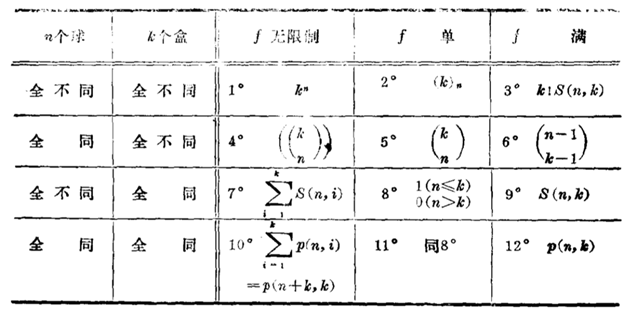
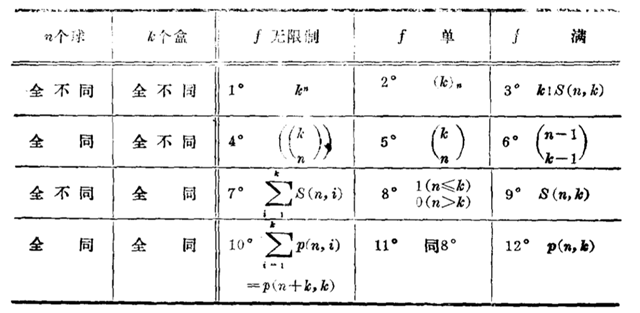
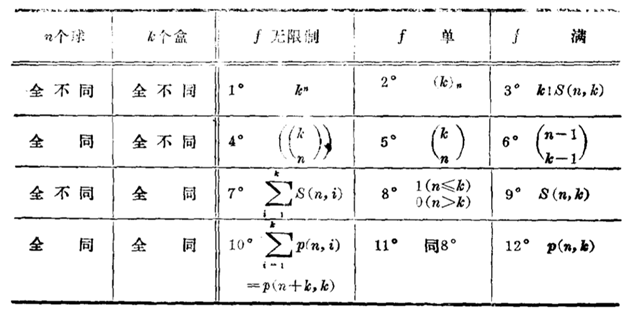
       经典计数之分配问题:把n个球放进k个盒子。考虑分配方法有三类:1.无限制 2.每个盒子至多一个（f 单的）3.每个盒子至少一个（f 满的）.球和盒子都只考虑两种极端情况：全同或全不同。这样一共会有3*2*2=12种分配情况,如下:

证明：

1.略 

2.此时只考虑$k\ge n$这种有意义情况，由分步计数原理易得$(k)_n=k(k-1)\cdots(k-n+1)$

3.此时只考虑$n\ge k$这种有意义情况,第一步将n球分成k部分有$S(n,k)$种方法，第二步

   分好的k部分球放到$k$个不同的盒子里有$k!$种排法.所以完成这件事情一共有$k!S(n,k)$种方法.

   这里$S(n,k)$定义如下：

  

4.方程$x_1+x_2+\cdots+x_k=n$的非负整数解.

5.此时只考虑$k\ge n$这种有意义情况，由于“f单”意味着每个盒子里至多放一个球，只需

    $k$个盒子里取$n$个，然后取出的盒子各放一个球。

6.方程$x_1+x_2+\cdots+x_k=n$的正整数解.

7.$n$元集至多分成$k$部分.

8.定义

9.$n$元集的$k$部分拆数为第二类$stirling$数$S(n,k)$

10.正整数$n$至多分成$k$个部分。这里分拆数$p(n,k)$定义如下：

注意：这里说的分拆是不计较各部的次序的，比如4的分拆为2,1,1一种。但4的有序分拆有三个(2,1,1);(1,2,1);(1,1,2).一般而言有序分拆好处理.比如$n$的$k$部有序分拆就是$x_1+x_2+\cdots+x_k=n$的正整数个数.

显然$p(n,1)=p(n,n-1)=p(n,n)=1;p(n,2)=[\frac{n}{2}]$，当$k>n$时$p(n,k)=0$一般的$p(n,k)$没有简单的表示方法.

           

注：$(n_1,n_2,\cdots,n_k)_{\ge}$表示$n_1\ge n_2\ge \cdots \ge n_k\ge1$

原则上所有$p(n,k)$可有递推式逐个求得，例如：

11.定义

12.只需考虑$n\ge k$的情况,正整数$n$的$k$部分拆$p(n,k)$

注：当然除了这12种情况外还有一些情况，比如盒子中有部分相同部分不同。但往往这样

       的情况的考察意义不大，因为很难期望会有一般的计数公式.