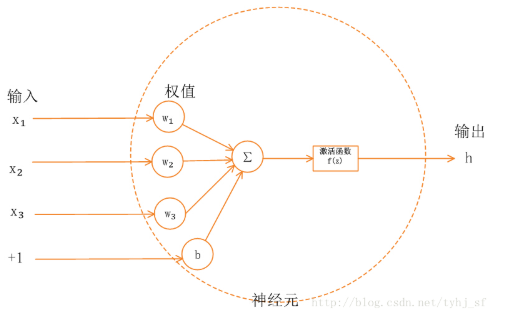
常用的激活函数
激活函数的主要目的是制造非线性。如果不用激励函数,每一层输出都是上层输入的线性函数,无论神经网络有多少层,输出都是输入的线性组合。
如果使用的话,激活函数给神经元引入了非线性因素,使得神经网络可以任意逼近任何非线性函数,这样神经网络就可以应用到众多的非线性模型中。
理论上来说,神经网络和多项式展开一样,或者傅里叶变换,通过一种方法来表达(或逼近)任意的函数,因此只有线性肯定是不够的,加上了非线性才能有表达非线性函数的能力。
softmax函数:定义Softmax函数,或称归一化指数函数,是逻辑函数的一种推广。它能将一个含任意实数的K维向量 ![]() “压缩”到另一个K维实向量
“压缩”到另一个K维实向量 ![]() 中,使得每一个元素的范围都在
中,使得每一个元素的范围都在 ![]() 之间,并且所有元素的和为1。实际上就是对数归一化,将实数映射到(0,1)之间,而且单调性不变,凸显其中最大的值并抑制远低于最大值的其他分量。
之间,并且所有元素的和为1。实际上就是对数归一化,将实数映射到(0,1)之间,而且单调性不变,凸显其中最大的值并抑制远低于最大值的其他分量。
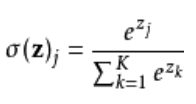
import math z = [1.0, 2.0, 3.0, 4.0, 1.0, 2.0, 3.0] z_exp = [math.exp(i) for i in z] print(z_exp) # Result: [2.72, 7.39, 20.09, 54.6, 2.72, 7.39, 20.09] sum_z_exp = sum(z_exp) print(sum_z_exp) # Result: 114.98 softmax = [round(i / sum_z_exp, 3) for i in z_exp] print(softmax) # Result: [0.024, 0.064, 0.175, 0.475, 0.024, 0.064, 0.175]
scores = np.array([123, 456, 789]) # example with 3 classes and each having large scores scores -= np.max(scores) # scores becomes [-666, -333, 0] p = np.exp(scores) / np.sum(np.exp(scores))
使用 Softmax 需要注意数值溢出的问题。因为有指数运算,如果 V 数值很大,经过指数运算后的数值往往可能有溢出的可能。所以,需要对 V 进行一些数值处理:即 V 中的每个元素减去 V 中的最大值。

Sigmoid函数:Sigmoid就是极端情况(类别数为2)下的Softmax 。优点是可以解释,比如将0-1之间的取值解释成一个神经元的激活率(firing rate)
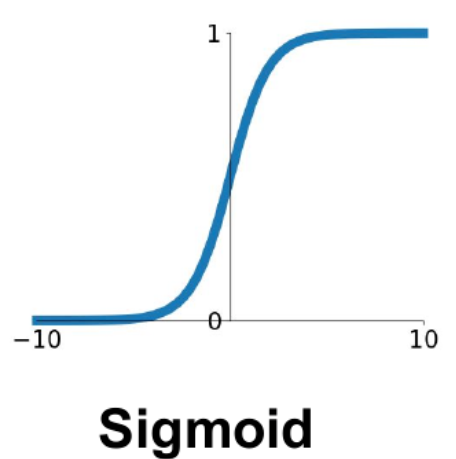
缺点:激活函数计算量大,反向传播求误差梯度时,求导涉及除法,反向传播时,很容易就会出现梯度消失的情况,从而无法完成深层网络的训练。Sigmoids函数饱和且kill掉梯度。Sigmoids函数收敛缓慢。
| 对比 | Softmax | Sigmoid |
| 公式 |
|
|
| 本质 | 离散概率分布 | 非线性映射 |
| 任务 | 多分类 | 二分类 |
| 定义域 | 某个一维向量 | 单个数值 |
| 值域 | [0,1] | (0,1) |
| 结果之和 | 一定为1 | 为某个正数 |
提问:softmax VS k个二元分类器
如果开发一个音乐分类的应用,需要对k种类型的音乐进行识别,那么是选择使用 softmax 分类器呢,还是使用 logistic 回归算法建立 k 个独立的二元分类器呢?
这一选择取决于类别之间是否互斥,例如,如果有四个类别的音乐,分别为:古典音乐、乡村音乐、摇滚乐和爵士乐,那么可以假设每个训练样本只会被打上一个标签(即:一首歌只能属于这四种音乐类型的其中一种),此时应该使用类别数 k = 4 的softmax回归。(如果在数据集中,有的歌曲不属于以上四类的其中任何一类,那么可以添加一个“其他类”,并将类别数 k 设为5。)
如果四个类别如下:人声音乐、舞曲、影视原声、流行歌曲,那么这些类别之间并不是互斥的。例如:一首歌曲可以来源于影视原声,同时也包含人声 。这种情况下,使用4个二分类的 logistic 回归分类器更为合适。这样,对于每个新的音乐作品 ,算法可以分别判断它是否属于各个类别。
一个计算视觉领域的例子,任务是将图像分到三个不同类别中。(i) 假设这三个类别分别是:室内场景、户外城区场景、户外荒野场景。会使用sofmax回归还是 3个logistic 回归分类器呢?
(ii) 现在假设这三个类别分别是室内场景、黑白图片、包含人物的图片,会选择 softmax 回归还是多个 logistic 回归分类器呢?
在第一个例子中,三个类别是互斥的,因此更适于选择softmax回归分类器 。而在第二个例子中,建立三个独立的 logistic回归分类器更加合适。
提问:softmax 反向梯度
其实就是对权重参数进行反向求导。softmax可以看做是一个线性分类器,求导过程的程序设计分为两种方法:一种是使用嵌套 for 循环,另一种是直接使用矩阵运算。
使用嵌套 for 循环,对权重 W 求导函数定义如下:
def softmax_loss_naive(W, X, y, reg):
"""
Softmax loss function, naive implementation (with loops)
Inputs have dimension D, there are C classes, and we operate on minibatches
of N examples.
Inputs:
- W: A numpy array of shape (D, C) containing weights.
- X: A numpy array of shape (N, D) containing a minibatch of data.
- y: A numpy array of shape (N,) containing training labels; y[i] = c means
that X[i] has label c, where 0 <= c < C.
- reg: (float) regularization strength
Returns a tuple of:
- loss as single float
- gradient with respect to weights W; an array of same shape as W
"""
# Initialize the loss and gradient to zero.
loss = 0.0
dW = np.zeros_like(W)
num_train = X.shape[0]
num_classes = W.shape[1]
for i in xrange(num_train):
scores = X[i,:].dot(W)
scores_shift = scores - np.max(scores)
right_class = y[i]
loss += -scores_shift[right_class] + np.log(np.sum(np.exp(scores_shift)))
for j in xrange(num_classes):
softmax_output = np.exp(scores_shift[j]) / np.sum(np.exp(scores_shift))
if j == y[i]:
dW[:,j] += (-1 + softmax_output) * X[i,:]
else:
dW[:,j] += softmax_output * X[i,:]
loss /= num_train
loss += 0.5 * reg * np.sum(W * W)
dW /= num_train
dW += reg * W
return loss, dW
使用矩阵运算,对权重 W 求导函数定义如下:
def softmax_loss_vectorized(W, X, y, reg): """ Softmax loss function, vectorized version. Inputs and outputs are the same as softmax_loss_naive. """ # Initialize the loss and gradient to zero. loss = 0.0 dW = np.zeros_like(W) num_train = X.shape[0] num_classes = W.shape[1] scores = X.dot(W) scores_shift = scores - np.max(scores, axis = 1).reshape(-1,1) softmax_output = np.exp(scores_shift) / np.sum(np.exp(scores_shift), axis=1).reshape(-1,1) loss = -np.sum(np.log(softmax_output[range(num_train), list(y)])) loss /= num_train loss += 0.5 * reg * np.sum(W * W) dS = softmax_output.copy() dS[range(num_train), list(y)] += -1 dW = (X.T).dot(dS) dW = dW / num_train + reg * W return loss, dW
实际验证表明,矩阵运算速度要比嵌套循环快很多,特别是在训练样本数量多的情况下。我们使用 CIFAR-10 数据集中约5000个样本对两种求导方式进行测试对比:
tic = time.time()
loss_naive, grad_naive = softmax_loss_naive(W, X_train, y_train, 0.000005)
toc = time.time()
print('naive loss: %e computed in %fs' % (loss_naive, toc - tic))
tic = time.time()
loss_vectorized, grad_vectorized = softmax_loss_vectorized(W, X_train, y_train, 0.000005)
toc = time.time()
print('vectorized loss: %e computed in %fs' % (loss_vectorized, toc - tic))
grad_difference = np.linalg.norm(grad_naive - grad_vectorized, ord='fro')
print('Loss difference: %f' % np.abs(loss_naive - loss_vectorized))
print('Gradient difference: %f' % grad_difference)
结果显示为:
naive loss: 2.362135e+00 computed in 14.680000s vectorized loss: 2.362135e+00 computed in 0.242000s Loss difference: 0.000000 Gradient difference: 0.000000
显然,此例中矩阵运算的速度要比嵌套循环快60倍。所以,当我们在编写机器学习算法模型时,尽量使用矩阵运算,少用 嵌套循环,以提高运算速度。(求线性回归的最小二乘解涉及矩阵求逆。在样本量大/维度高的情况下计算量较大。这时可以使用梯度下降法近似来求最小二乘解。)
实际上,这又回归到解方程,线性代数那部分知识去了,如果通常来说参数比样本少,多元方程肯定有解,如果参数太多,多余样本,也可以找到一个较小的loss值作为求参结束的标志。参考以下网址:http://cs231n.github.io/classification/
https://blog.csdn.net/red_stone1/article/details/80687921
ReLU函数:
输入信号 <0 时,输出都是0,>0 的情况下,输出等于输入。Krizhevsky et al. 发现使用 ReLU 得到的 SGD 的收敛速度会比 sigmoid/tanh 快很多。
ReLU更容易学习优化。因为其分段线性性质,导致其前传,后传,求导都是分段线性。而传统的sigmoid函数,由于两端饱和,在传播过程中容易丢弃信息。
ReLU激活函数在AlexNet[3]中大放异彩,使用ReLU作为激活函数的网络比使用tanh作为激活函数的网络收敛快6倍。这个时候大家突然发现激活函数的主要目的是制造非线性,有没有生物学解释其实不那么重要,函数光滑不光滑也没那么重要。
缺点:训练的时候很”脆弱”,很容易就”die”了,还是非zero-centered。非zero-centered会导致后一层的神经元将得到上一层输出的非0均值的信号作为输入。 产生的一个结果就是对w求局部梯度则都为正,
这样在反向传播的过程中w要么都往正方向更新,要么都往负方向更新,导致有一种捆绑的效果,使得收敛缓慢。详细可以参考:https://www.jianshu.com/p/917f71b06499
例如,一个非常大的梯度流过一个 ReLU 神经元,更新过参数之后,这个神经元再也不会对任何数据有激活现象了,那么这个神经元的梯度就永远都会是 0.
如果 learning rate 很大,那么很有可能网络中的 40% 的神经元都”dead”了。

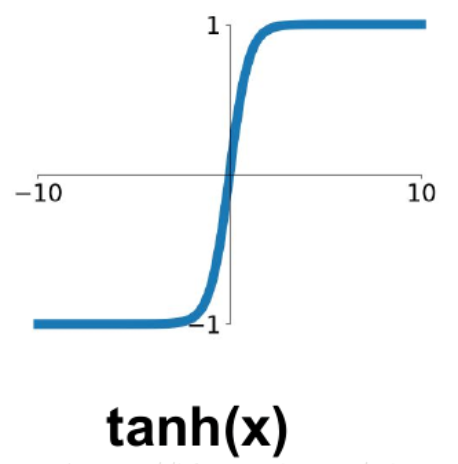
Tanh函数:
也称为双切正切函数,取值范围为[-1,1]。
tanh在特征相差明显时的效果会很好,在循环过程中会不断扩大特征效果。
与 sigmoid 的区别是,tanh 是 0 均值的,因此实际应用中 tanh 会比 sigmoid 更好,但是虽然tanh是zero-centered,但是还是会饱和。
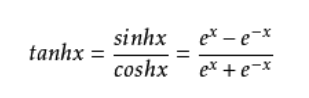
Maxout函数:
maxout是通过分段线性函数来拟合所有可能的凸函数来作为激活函数的,但是由于线性函数是可学习,所以实际上是可以学出来的激活函数。具体操作是对所有线性取最大,也就是把若干直线的交点作为分段的界,然后每一段取最大。
maxout可以看成是relu家族的一个推广。
缺点在于增加了参数量。
结尾: 应用中如何选择合适的激活函数?
这个问题目前没有确定的方法,凭一些经验吧。
1)深度学习往往需要大量时间来处理大量数据,模型的收敛速度是尤为重要的。所以,总体上来讲,训练深度学习网络尽量使用zero-centered数据 (可以经过数据预处理实现) 和zero-centered输出。所以要尽量选择输出具有zero-centered特点的激活函数以加快模型的收敛速度。
2)如果使用 ReLU,那么一定要小心设置 learning rate,而且要注意不要让网络出现很多 “dead” 神经元,如果这个问题不好解决,那么可以试试 Leaky ReLU、PReLU 或者 Maxout.
3)最好不要用 sigmoid,你可以试试 tanh,不过可以预期它的效果会比不上 ReLU 和 Maxout.



