聚类算法
聚类算法有很多,常见的有几大类:划分聚类、层次聚类、基于密度的聚类。本篇内容包括k-means、层次聚类、DBSCAN 等聚类方法。
k-means 方法
- 初始k个聚类中心;
- 计算每个数据点到聚类中心的距离,重新分配每个数据点所属聚类;
- 计算新的聚簇集合的平均值作为新的聚类中心;
- 迭代,直到不再重新分配.
k-means 损失函数
设k个聚类中心为\(\mu_1,\mu_2,\dots,\mu_k\),用\(r_{nk}\in \{0,1\}\)表示\(x_n\)是否属于聚类k.则损失函数定义为:
其表征了数据的混乱度.
最小化损失函数的过程是一个NP问题,而k-means的迭代过程是一个收敛到局部最低点的过程.
k的选定
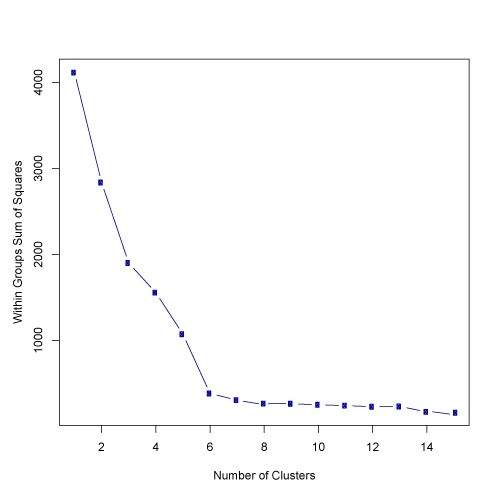
"肘点"法:
选取不同的k值,画出损失函数,选取突然变缓的地方的k值.
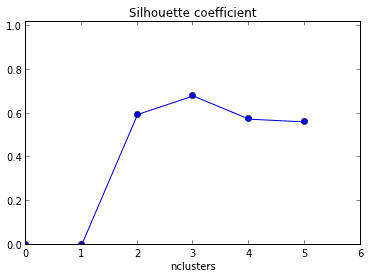
轮廓系数:旨在将某个对象与自己的簇的相似程度和与其他簇的相似程度进行比较。轮廓系数最高的簇的数量表示簇的数量的最佳选择。如下图的最高点:
初始化方法
k-means初始化方法包括 Forgy 和随机分区。Forgy 方法从数据集中随机选择k个观测值,并将其作为初始值。随机分区方法是先随机为每个观测值分配一个簇,随后进行更新,簇的随机分配点的质心就是计算后得到的初始平均值。
异常点免疫
一些异常点可能严重影响聚类中心,可以通过一些调整来减少影响,比如中心点不取均值,而是取离均值最近的样本点(中值k-median,又称k-medoids). k-medoids 对每个聚簇选取中心点时需要再遍历一遍聚簇,因此增加O(n)的计算量. k-medoids 相比 k-means 对于噪声数据不再敏感.
k-means优缺点
优点:简单,速度快
缺点:最终的聚类结果严重依赖于初始点选择,容易陷入局部最优(与简单的爬山算法容易陷入局部最优类似),并且需要提前知道k的值.
- 存储空间大
- 时间复杂度高(要分类的实例需与所有已知实例比较)
- 样本分布不均衡时,k近邻容易被错误归类
针对第三个缺点的改进: 计算相似度时加上与距离相关的权重(如距离的倒数).
初始聚类中心敏感
缓解办法:
- 初始第一个中心为某点后初始第二个点时选择离他最远的点,后面的点选择离这些点最远的点.
- 多初始化几遍,选择损失最小的(sklearn等库通常会有此参数)
- 采用k-means++等优化的初始化聚类方法.
k-means++
与k-means相比,改进之处在于初始中心集合的选择:
- 初始中心点集合为空.
- 从数据点中随机选第一个中心点.
- 重复以下过程选出k个初始中心
- a) 计算每个数据点到其最近的中心点的距离D.
- b) 以正比于D的概率(轮盘赌选择法),随机选择一个新数据点加入中心点集合中.
k-means++算法的缺点
虽然k-means++算法可以确定地初始化聚类中心,但是从可扩展性来看,它存在一个缺点,那就是它内在的有序性特性:下一个中心点的选择依赖于已经选择的中心点。 针对这种缺陷,k-means||算法提供了解决方法。
k-means||[1]
k-means||是对k-means++的一种并行化实现, 在Spark ML框架中做了实现. k-means||算法来自12年的论文Scalable K-Means++.
k-means||算法是在k-means++算法的基础上做的改进,和k-means++算法不同的是,它采用了一个采样因子l,并且l=A(k),在spark的实现中l=2k。这个算法首先如k-means++算法一样,随机选择一个初始中心, 然后计算选定初始中心确定之后的初始花费\(\psi\)(指与最近中心点的距离)。之后处理\(log(\psi )\)次迭代,在每次迭代中,给定当前中心集,通过概率\(ld^{2}(x,C)/\phi_{X}(C)\)来 抽样x,将选定的x添加到初始化中心集中,并且更新\(\phi_{X}(C)\)。该算法的步骤如下图所示:
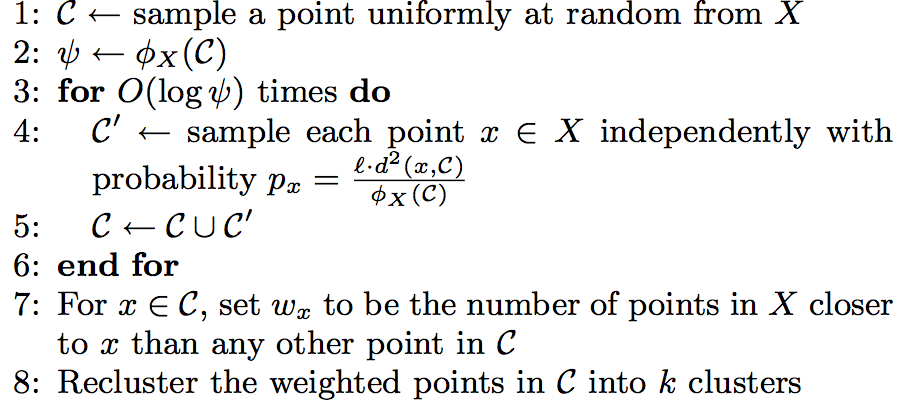
第1步随机初始化一个中心点,第2-6步计算出满足概率条件的多个候选中心点C,候选中心点的个数可能大于k个,所以通过第7-8步来处理。第7步给C中所有点赋予一个权重值\(w_{x}\) ,这个权重值表示距离x点最近的点的个数。 第8步使用本地k-means++算法聚类出这些候选点的k个聚类中心。在spark的源码中,迭代次数是人为设定的,默认是5。
该算法与k-means++算法不同的地方是它每次迭代都会抽样出多个中心点而不是一个中心点,且每次迭代不互相依赖,这样我们可以并行的处理这个迭代过程。由于该过程产生出来的中心点的数量远远小于输入数据点的数量, 所以第8步可以通过本地k-means++算法很快的找出k个初始化中心点。何为本地k-means++算法?就是运行在单个机器节点上的k-means++。
Mini Batch K-Means
Mini Batch K-Means算法是K-Means算法的变种,采用小批量的数据子集减小计算时间,同时仍试图优化目标函数,这里所谓的小批量是指每次训练算法时所随机抽取的数据子集,采用这些随机产生的子集进行训练算法,大大减小了计算时间,其产生的结果,一般仅略差于标准算法。
该算法的迭代步骤有两步:
- 从数据集中随机抽取一些数据形成小批量,把他们分配给最近的质心
- 更新质心
与K均值算法相比,数据的更新是在每一个小的样本集上。对于每一个小批量,通过计算平均值得到更新质心,并把小批量里的数据分配给该质心,随着迭代次数的增加,这些质心的变化是逐渐减小的,直到质心稳定或者达到指定的迭代次数,停止计算.Mini Batch K-Means比K-Means有更快的收敛速度,但同时也降低了聚类的效果,但是在实际项目中却表现得不明显.
层次聚类
假设有个待聚类的样本,对于层次聚类来说,步骤(与霍夫曼编码过程类似,自下而上构建树):
- (初始化)把每个样本归为一类,计算每两个类之间的距离
- 寻找各个类之间最近的两个类,把它们归为一类
- 重新计算新生成的这个类与各个旧类之间的相似度
- 重复2和3直到所有样本点都归为一类,结束。
整个聚类过程建立了一棵树,在建立的过程中,可以通过在第二步上设置一个阈值,当最近的两个类之间的距离大于这个阈值,则认为迭代可以终止。
两个类之间的距离(相似度)有多种计算方法:
- SingleLinkage,又叫nearest-neighbor,就是取两个类中距离最近的两个样本的距离作为这两个集合的距离。
- CompleteLinkage,与SingleLinkage正相反,取两个集合中距离最远的两个点的距离作为两个集合的距离。其效果也是刚好相反。
- Average-linkage:这种方法就是把两个集合中的点两两的距离全部放在一起求一个平均值,相对也能得到合适一点的结果。这种方法的一种变种就是取两两距离的中值,与取均值相比更加能够解除个别偏离样本对结果的干扰。
- ward是一种质心算法。质心方法通过计算集群的质心之间的距离来计算两个簇的接近度。对于 Ward 方法来说,两个簇的接近度指的是当两个簇合并时产生的平方误差的增量。
表示每个点x到合并后簇中心点的距离,平方后加起来,又称error sum of squares(ESS),等于 \(n\times \text{Var}(X)\) 。
通过观察树状图,可以很好的判断出不同组的簇数。根据下图,水平线贯穿过的树状图中垂直线的数量将是簇数的最佳选择,这条线保证了垂直横穿最大距离并且不与簇相交。
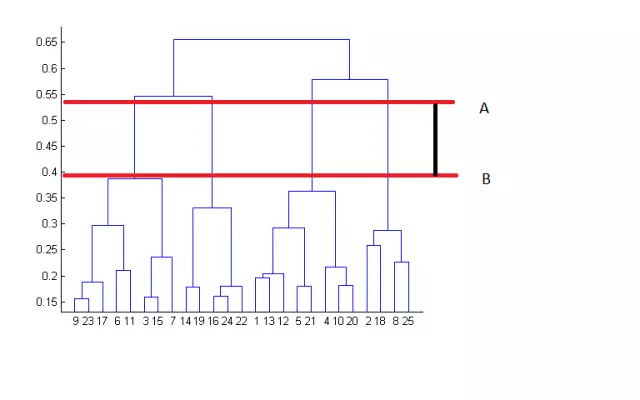
在图中的例子中,簇的数量最佳选择是4,因为红色水平线涵盖了最大的垂直距离AB。
BIRCH 聚类
BIRCH 聚类特征树的构造是不断插入对象节点的过程, 对树从上到下进行比较,插入节点后如果某节点的孩子节点数超出限制,则进行分裂.分裂规则是选出蔟间距最大的两个孩子作为两个子节点,其它孩子就近分配.
BIRCH 聚类算法可以在任何内存下运行,主要用于处理超大规模数据集,是基于距离的层次聚类。只需扫描一遍构造聚类特征树,比较快速。缺点:不适合非球形簇;对高维数据不好;结果依赖于数据点的插入顺序。
层次聚类与k-means的比较:
k-means的计算复杂度只有\(O(tkn)\),t是迭代次数,k是设定的聚类数目,而n是数据量,相比起很多其它算法,k-means算是比较高效的。但是k的值往往不容易确定,用户如果选择了不正确的聚类数目,会使得本应同一个cluster的数据被判定为属于两个大的类别,这是我们不想看到的。因为需要数据点的坐标,这个方法的适用性也受到限制。但是效率是它的一个优势,在数据量大或者对聚类结果要求不是太高的情况下,可以采用k-means算法来计算,也可以在实验初期用来做测试看看数据集的大致情况。
而层次聚类则不适合大数据, 对异常点敏感。层次聚类时间复杂度\(O(n^3)\),形式很像哈夫曼编码,可解释性较好。
下面介绍基于密度的聚类方法: DBSCAN 与 mean-shift.
DBSCAN
DBSCAN(Density-Based Spatial Clustering of Applications with Noise) 是一种基于密度的聚类算法, 包括两个变量, 半径范围eps, 半径内指定的点的数目minPts.
基本思想是以某点为核心,在指定半径范围内拥有超过指定点数的点形成一个簇. 将核心点周围密度可达的点中满足指定半径范围内拥有超过指定点数minPts的点标记为已访问,而将指定半径范围内小于minPts标记为噪声点. 重复此过程直到所有点都被标记.
DBSCAN的主要优点有:
- DBSCAN聚类算法基于点的密度,不需要确定簇的数量。
可以对任意形状的稠密数据集进行聚类,相对的,K-Means之类的聚类算法一般只适用于凸数据集。 - 可以在聚类的同时发现异常点,对数据集中的异常点不敏感。
- 聚类结果没有偏倚,相对的,K-Means之类的聚类算法初始值对聚类结果有很大影响。
DBSCAN的主要缺点有:
- 对于高维数据不能很好地反映;
不能很好用于密度不断变化的数据集中。如果样本集的密度不均匀、聚类间距差相差很大时,聚类质量较差,这时用DBSCAN聚类一般不适合。 - 如果样本集较大时,聚类收敛时间较长,此时可以对搜索最近邻时建立的KD树或者球树进行规模限制来改进。
- 调参相对于传统的K-Means之类的聚类算法稍复杂,主要需要对距离阈值,邻域样本数阈值MinPts联合调参,不同的参数组合对最后的聚类效果有较大影响。
均值漂移(mean-shift)
mean-shift 是一种非参数估计算法,它将每个数据点划归到近邻当中密度最高的簇.
由于用核密度估计方法计算密度,时间开销较大, mean-shift 通常比 DBSCAN 或 质心法速度慢.
每个数据点\(x^{(l)}\in R^d\)的近邻密度为:
其中,h为带宽(半径), 是唯一需要调节的参数, h较小,则得到的簇的数量较多, h较大,则得到的簇的数量较少; K为核函数, 常见形式有:
- 高斯核: \(K(x^{(i)})=e^{-(x^{(i)})^2\over 2\sigma^2}\)
- Epanechnikov 核: \(K(x^{(i)})={3\over 4}(1-(x^{(i)})^2) \text{ if } |x^{(i)}|\le 1 \text{ else 0}\)
mean-shift 通过对\(f(x^{(l)})\)求导,迭代计算,得到\(f(x^{(l)})\)的最大值.
衡量指标
可以使用误差平方和(sum of squared error,SSE),又称散度(scatter)来度量聚类之后所有簇的质量,越小越好.
其它的评估聚类质量的方法有:轮廓系数(silhouette cofficient):
\(d_s(i)\) 为每个数据点i与同簇各数据点之间的平均距离;
\(d_{rest}(i)\) 为每个数据点i与其它各簇数据点之间的最小距离.
所有数据点的平均轮廓系数为总轮廓系数, 其值越接近于1越好;越接近-1越差.
如果能够得到数据真正的标签,则可以计算同质性和完整性,及其调和均值. 但是往往我们很难得到标签.
聚类分析
聚类分析(cluster analysis),是一种现代统计学分析方法,其划分方式有多种:
-
根据分类对象的不同,可以分为:Q型聚类分析和R型聚类分析。
- 对样本进行研究称为样本聚类或Q型聚类;
- 对变量即观测指标进行研究,称为变量聚类或R型聚类.
R型聚类通过了解变量间的相似程度和亲疏关系,以此选出有代表性的变量,从而达到降维的效果,同时,也可以对结果再进行Q型聚类.
-
按照分析方法的不同,又可以分为:系统聚类法、快速聚类法和模糊聚类法。k-means就是快速聚类法中的一种。

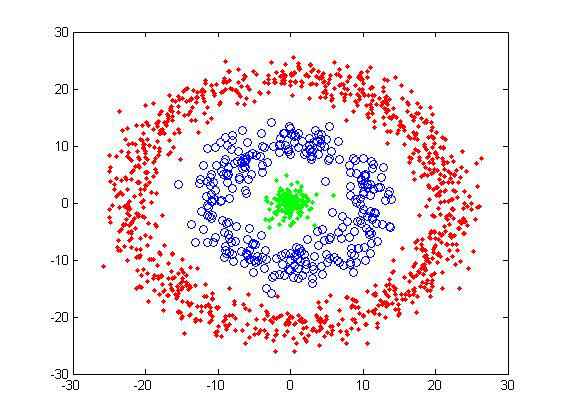 本篇内容包括划分聚类方法中的k-means、k-means++,基于密度的DBSCAN以及层次聚类等聚类方法。
本篇内容包括划分聚类方法中的k-means、k-means++,基于密度的DBSCAN以及层次聚类等聚类方法。

