博客作业06--图
一.学习总结(2分)
1.1查找的思维导图
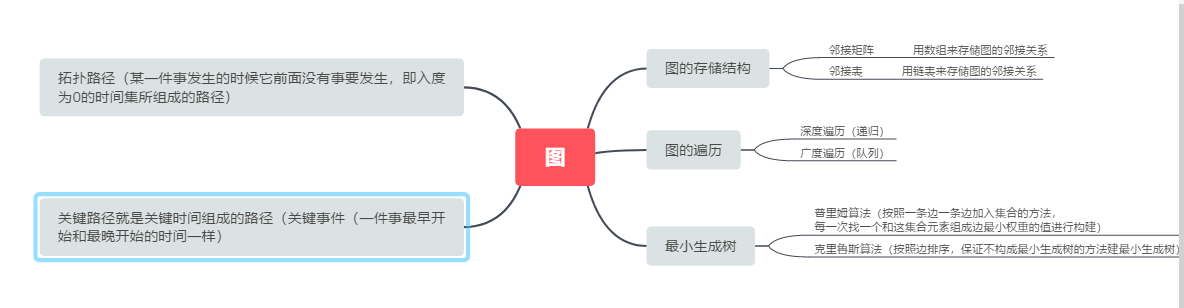
1.2 查找学习体会
深度遍历算法
遍历源节点所在的边
记录第一个和源节点有邻接关系的点记为s
if(s没被访问)访问递归访问s所在的链
否则返回
遍历顺序
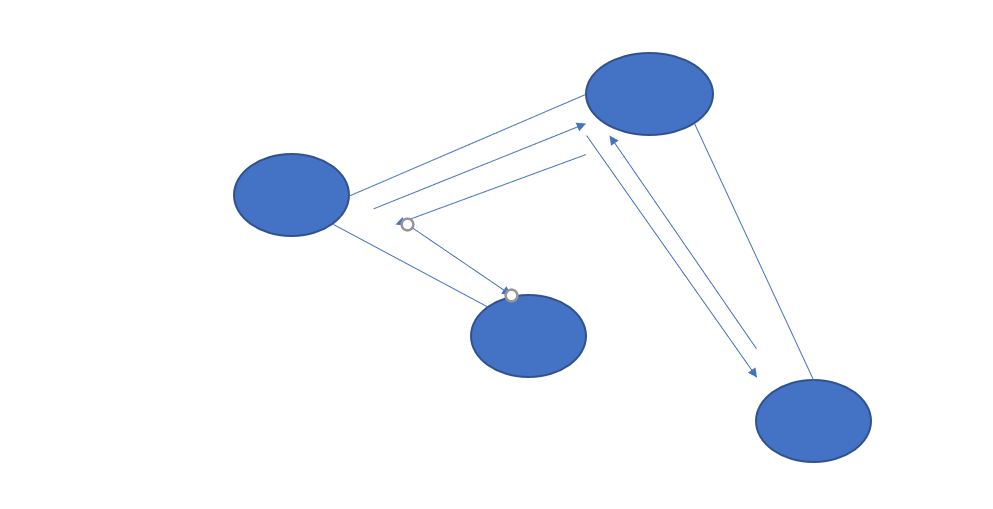
广度遍历算法
遍历源节点的所有边并且入队
while(队不空)
{s=队头
出队
if(s没被访问){
将与s有邻接关系且同时没有被反问过的进行入队
}
}
遍历顺序
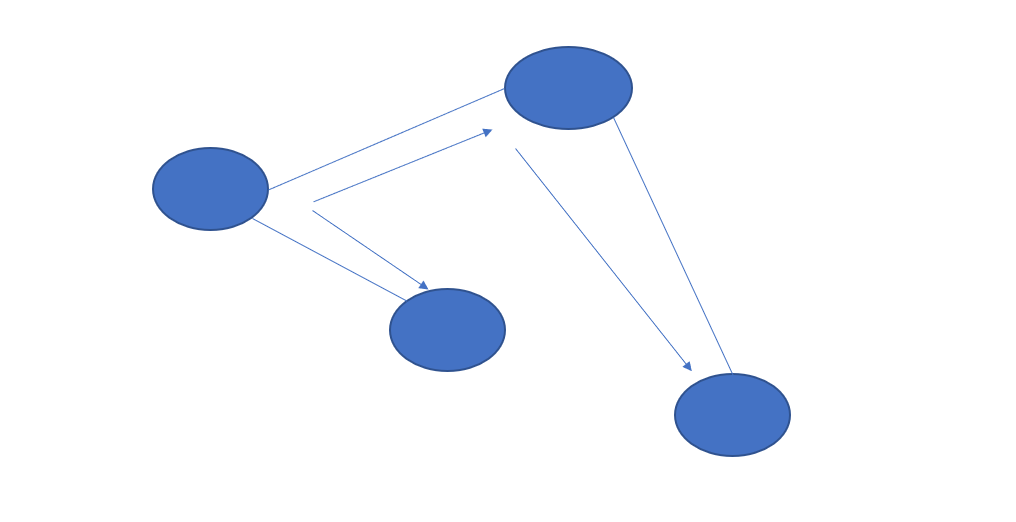
Prim和Kruscal算法
二者都是对贪心算法的改进而生成的算法
针对以下数据生成的最小生成树顺序
0 1 1
1 3 2
0 2 3
1 2 4
2 3 1
prim算法<0,1><1,3><2,3>
Kruscal算法<0,1><2,3><1,2>
Dijkstra算法
初始化数组path[]=-1,dist[无穷大],s[]=0;
将源的s[]置1
更新dist和path
u=源点;
while(i<g.n){
找到与源点有邻接关系的dist中的最小值
u=i;
while(j<g.n){
if(dist[u]>dist[j]+g[u][j])更新dist数组
}
拓扑排序算法
初始化每个元素的入度为0
遍历每一条链来统计每个数的入度
入度为0入队
while(队不空){
遍历队头所在的链,减少对应的点的入度
入度为0入队}
二.PTA实验作业(4分)
7-3 六度空间(30 分)
1 设计思路(伪代码或流程图)
定义每一层次的队尾为last,层次为u=0
遍历源节点的所有边并且入队
last=源节点
u++;
while(队不空&&u<=6)
{s=队头
出队
if(s没被访问){
将与s有邻接关系且同时没有被反问过的进行入队
}
if(s==last)last=队尾,u++
}
2.代码截图
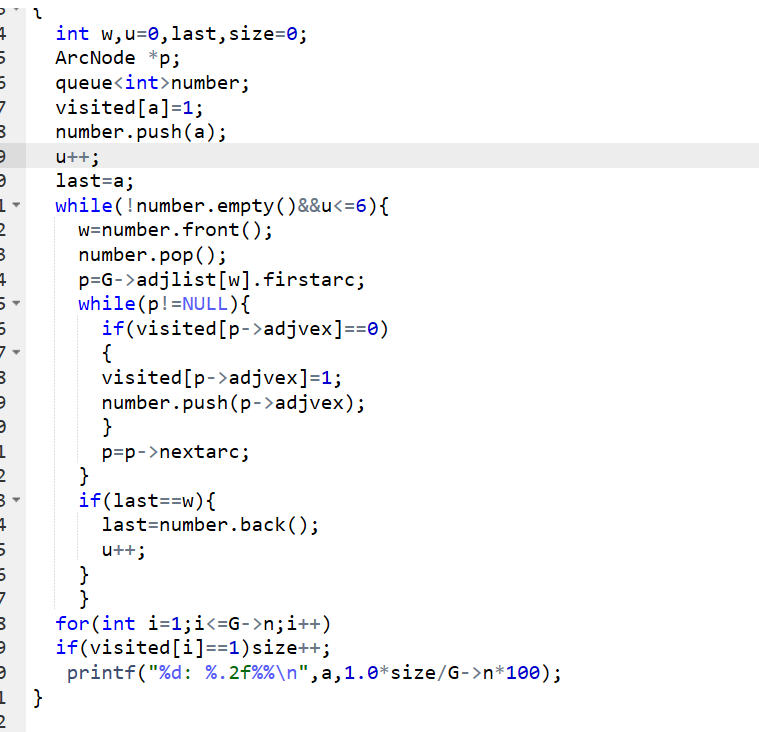
3.PTA提交列表说明

自己打还好考试的时候没注意数据量用了矩阵做最后一个点过不去
7-5 畅通工程之最低成本建设问题(30 分)
1 设计思路(伪代码或流程图)
prim算法
/*初始化访问数组vis代表是否加入到最小生成树,
初始化权重数组d为无穷*/
将源点的vis置为1,更新与原点有邻接关系的节点的权重数组
for(int i=1;i<=n;i++)
{
u=-1;
min=inf;
找寻d数组中的最小值
并记录最小值对应的下标。
if(u==-1)说明该图不能够连同return-1
else vis[u]=true;
路径叠加
for(int v=1;v<=n;v++)
if(G[u][v]<d[v])
更新dis数组
}
2.代码截图
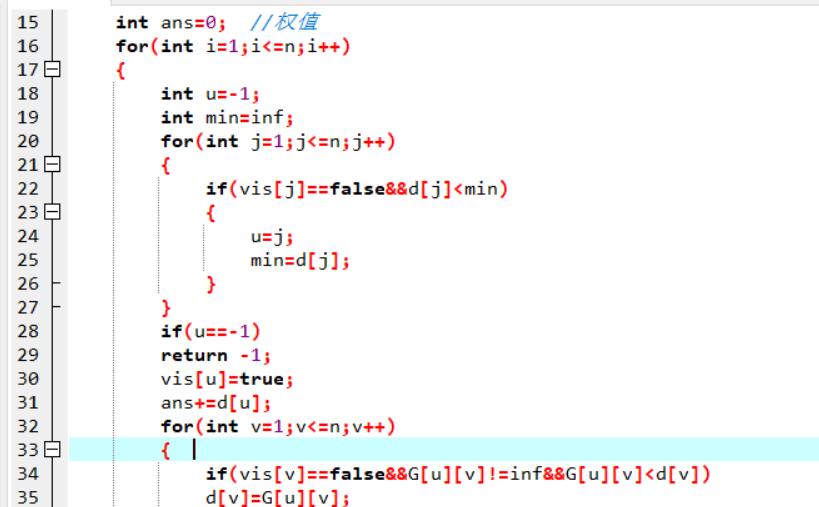
3.PTA提交列表说明
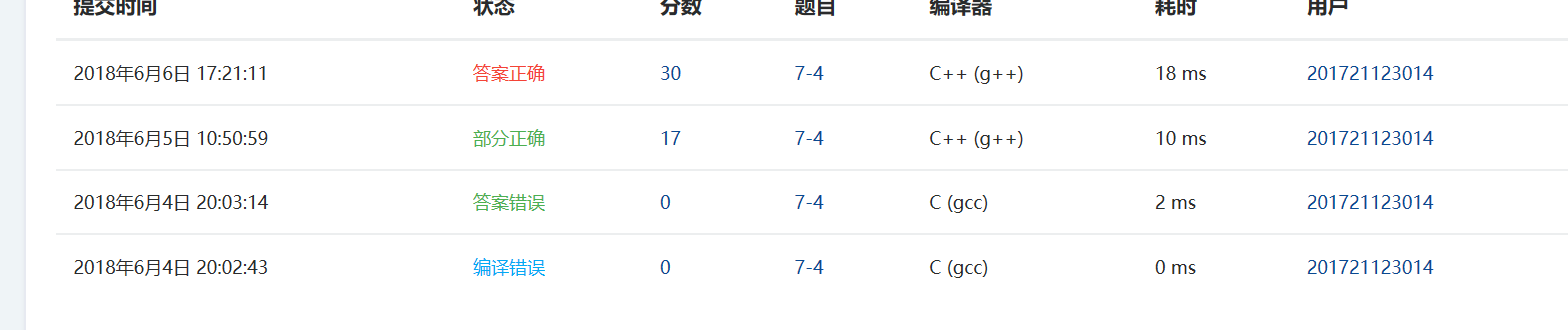
前面瞎写了一下后面参考书本更改了
7-8 城市间紧急救援(25 分)
1 设计思路(伪代码或流程图)
初始化数组path[]=-1,dist[无穷大],s[]=0;
初始化记录路径总数的ans为0
将源的s[]置1
更新dist和pathans
u=源点;
while(i<g.n){
找到与源点有邻接关系的dist中的最小值
u=i;
while(j<g.n){
if(dist[u]>dist[j]+g[u][j].weight)更新dist数组,ans数组
else if(dist[u]==dist[j]+g[u][j].weight){
更新dist数组ans数组
}
}
if(
2.代码截图

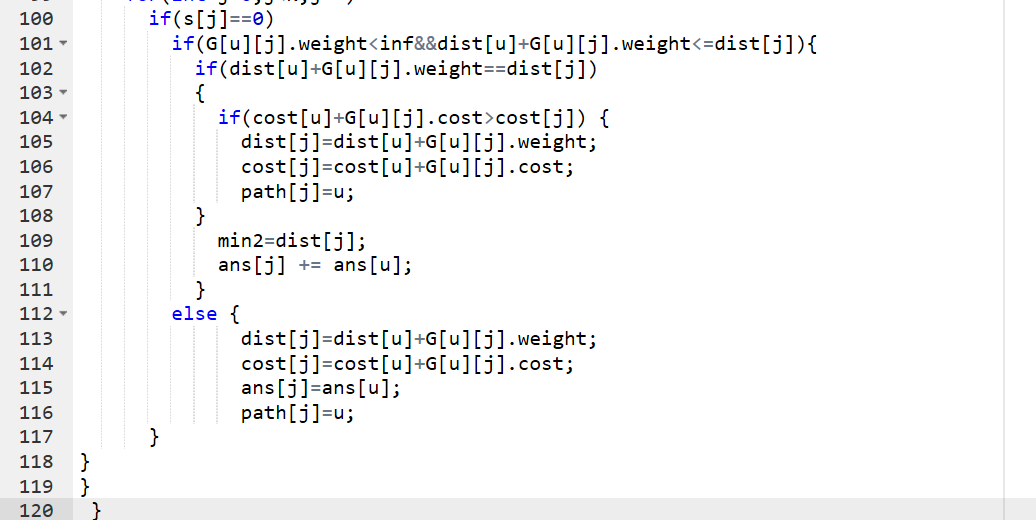
3.TA提交列表说明
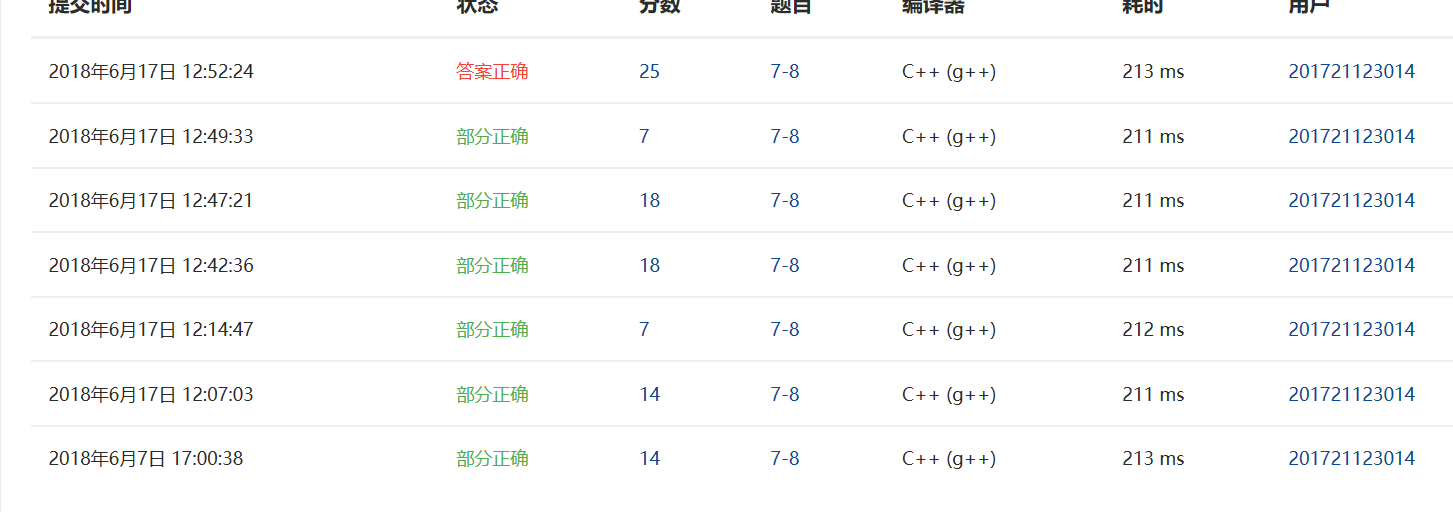
这个路径的数目没有就解决一开始后面用叠加一下就可以解决
三.截图本周题目集的PTA最后排名(3分)
3.1 PTA排名

3.3 我的总分:277
四. 阅读代码(必做,1分)
图的代码太长找了个比较感兴趣的代码
http://acm.hdu.edu.cn/showproblem.php?pid=1147
题意是在一个平面上按顺序摆上放一些棍子,求最后哪些棍子在最上面(此题只需考虑规范相交的情况)这样我们只要判断这些棍子是否相交相交就是往上面
叠起来的意思
/**
*判断后面的线段是否与前面的线段相交,
*此题还是一个判断线段是否相交的问题,
*只是必须注意顺序,判断相交的函数减hdu1086
*/
#include<iostream>
#include<cstring>
#include<cmath>
using namespace std;
typedef struct Node{
double x,y;
}node;
node p[100005],p1[100005];
double Direction(node pi,node pj,node pk){//计算叉乘
return (pk.x-pi.x)*(pj.y-pi.y)-(pj.x-pi.x)*(pk.y-pi.y);
}
bool Segments_X(node p1,node p2,node p3,node p4){//判断两条线段是否相交,相交返回true
double d1,d2,d3,d4;
d1=Direction(p3,p4,p1);
d2=Direction(p3,p4,p2);
d3=Direction(p1,p2,p3);
d4=Direction(p1,p2,p4);
if(d1*d2<=0&&d3*d4<=0) return true;
return false;
}
int main()
{
int n;
while(cin>>n&&n){
for(int i=1;i<=n;i++){
cin>>p[i].x>>p[i].y;//输入第一个点
cin>>p1[i].x>>p1[i].y;//输入第二个点
}
cout<<"Top sticks: ";
for(int i=1;i<n;i++){
int ok=1;
for(int j=i+1;j<=n;j++){//之判断在该线段之后抛下的线段(木棍)
if(Segments_X(p[i],p1[i],p[j],p1[j])){
ok=0; break;
}
}
if(ok) cout<<i<<", ";
}
cout<<n<<"."<<endl;//输出最后一个
}
return 0;
}
这道题目难的不是解题可能更难的是看懂题目
就是利用数学去判断线段是否相交
五. 代码Git提交记录截图



